基于养护成本的高速公路收费费率问题研究

林文新,王建伟,林渝钧

(1.长安大学经济与管理学院,西安710064;2.深圳高速公路股份有限公司,广东深圳518026)

基于养护成本的高速公路收费费率问题研究

林文新1,2,王建伟*1,林渝钧2

(1.长安大学经济与管理学院,西安710064;2.深圳高速公路股份有限公司,广东深圳518026)

高速公路收费到期或政府回购后可能面临路面交通拥堵、道路设施养护成本上升等诸多问题,以养护道路为目的降低收费标准继续收费是减缓地方财政压力和减少社会舆论压力的可行方法之一.本文从养护成本的角度出发,建立了双层规划模型.上层规划中将路网管理者(政府)作为领导者,以高速公路承载的交通流量最大,而路网总延误最小为目标函数,同时考虑代为管理者(运营方)的合理收益和养护成本支出的最低收费标准及道路使用者所能接受的最高收费标准.下层规划则在充分考虑道路使用者的路径选择差异性及道路拥堵对交通分布影响的基础上,建立用户均衡模型.最后采用模拟退火算法验证模型并得出具有参考意义的收费费率值.

公路运输;收费费率;双层规划模型;养护成本;模拟退火算法

1 引 言

高速公路是现代交通的重要标志,对我国国民经济增长和社会的蓬勃发展发挥了重要作用.2012年1月1日,中国大陆的第一条高速公路S5沪嘉高速公路调整为城市快速路并停止收费,这标志着高速公路收费到期后的路网管理正式拉开序幕.因社会舆论以及继续刺激经济发展的需要,政府回购高速公路也逐步被提上议程.但是,高速公路收费到期或者政府回购后可能面临路面交通拥堵、超限车辆管理难度增加、道路设施养护成本上升等诸多问题,以养护道路的目的降低收费标准继续收费是缓解地方财政压力和减少社会舆论压力的可行方法之一.

以养护道路的目的降低收费标准继续收费,即高速公路养护型收费,是一种由政府作为路网管理者,运营方作为代理管理者,以养护道路及保障高速公路高速便捷性为目的,同时考虑养护成本及运营方的合理收益的过渡性收费模式.

针对高速公路收费标准的制定问题,国内专家提出了一系列的方法.文献[1]主要是考虑投资总额,并结合影响高速公路收费标准的各种因素建立了收费标准模型;文献[2]从高速公路使用者的角度出发,采用级差收益法对某段高速公路的收费标准进行了测算和研究,提出了最佳的收费率;文献[3]通过对特大城市高速公路城区段的交通特征分析,基于拥挤收费的研究角度提出了双层规划的收费模型;文献[4]在充分考虑运营方及出行者的利益、路网的运行效率和高速公路的公共物品特性的基础上,建立双层规划模型并最终验证优化模型的实用性;文献[5]则是在探讨固定需求下公路收费标准与路网交通量分配关系的基础上,利用双层规划模型来描述收费标准的制定问题;文献[6]则是将拥挤收费与高速公路费率问题结合在一起,并最终采用双层规划模型计算弹性需求下高速公路拥挤收费费率.

上述文献均试图通过科学合理的手段确定最优最适合各方利益的高速公路收费费率,但随着时代及高速公路政策的改变,研究方法与未来实际需求相差甚远.本文在结合当今高速公路发展趋势及未来高速公路的功能定位的基础上,另辟蹊径,提出采用基于养护成本的高速公路收费费率模式,有一定的研究意义与实际价值.

2 模型构建及算法设计

基于养护成本的高速公路收费模式,因没有建设投资及还贷压力的影响,因此交通管理者(政府)在考虑收费费率的制定问题上可以更多地从路网最优化的角度出发,仅需保证部分资金的回收以支撑养护及管理成本.经比较高速公路收费费率的制定方法,并结合本文的出发点以及最终目的,采用双层规划模型解决基于养护成本的高速公路收费费率问题.

双层规划是一种具有双层梯阶结构的决策优化模型,上层问题和下层问题都有各自的目标函数和约束条件.上层问题的目标函数和约束条件不仅与上层决策变量有关,同时还取决于下层问题的最优解,而下层问题的最优解又受上层决策变量的影响.

2.1 养护成本及管理成本

高速公路养护是指高速公路建成通车投入运营后,进行经常性、及时性和预防性的日常养护,以确保高速公路上的各种工程及设施,如路基、路面、桥涵、隧道、安全设施等持续处于良好的技术状态.而高速公路运营管理主要是指高速公路建成通车后,对高速公路的收费、养护、交通、安全、服务等系统进行计划、组织、指挥、控制和协调[7].共同为实现高速公路快捷、畅通、安全、舒适、经济的使用功能服务.

由于目前没有高速公路运营管理费用的相关规定,管理成本参考近年高速公路公司实际运营开支情况.

养护成本与道路车道数量、通车年数、交通量、桥隧比例以及大修有关.计算参考《广东省高速公路大小修费用标定模型研究》,

养护费用模型为

大修费用模型为

式中 Y表示养护费用万元/(公里·年);K日表示日常维修费用系数,1.6≤K日≤2.51;K车道表示车道修正系数;K固定表示固定资产投资价格指数;X1表示通车年数;X2表示交通量(Pcu/d); X3表示桥隧比;X4、X5表示路面类型的虚拟变量.

2.2 基本假设

对于高速公路收费,出行者会根据收费费率的不同及高速公路的服务状态(主要表现为时效性)来选择自己的出行,最终路网达到一种平衡状态.交通管理者所认为的最优收费费率,是促使路网达到最优状态的结果.因此,本文对于高速公路收费费率的研究,基于以下假设:

(1)由于高速公路有其特定的行驶工具(汽车),区段间的有交通需求的出行者不会因为收费费率的降低而改变其原有的交通方式(地铁、公交等);

(2)出行者在使用高速公路时,能够对高速公路和其他公路的流量信息有清楚了解,并进行理性选择;

(3)出行者不会因为高速公路出入口设置地点问题而选择出入更为便利的普通道路;

(4)交通管理者将适度平衡区域内交通网络,不可能出现交通流量的完全集中化,现假设路网普通公路车流量不得低于总交通需求的10%.

2.3 双层规划模型

一般情况下,出行者总是会选择从起点到终点之间广义费用最低的交通方式.同时,出行费用是随着交通量的增长而上升的,最终达到客流分配的稳定均衡状态.

上层模型:

式中 N表示交通网络中节点的集合;W表示交通网络中路段的集合;qωn表示在OD对ω间第n种运输方式上的标准车型交通流量;uωn表示在OD对ω间第n种运输方式上的通行费费率;tn(*)表示行驶时间延误函数;qωn(uωn)表示在OD对ω间第n种运输方式的交通量与通行费费率的函数; Cωn表示在OD对ω间第n种运输方式的通行能力;在lωn表示在OD对ω间第n种运输方式的里程; Un表示在OD对ω间第n种运输方式的养护成本及管理成本之和.

下层模型:

式中 Qω表示在OD对ω间的交通需求量;fωn(x)表示在OD对ω间第n种运输方式的广义费用函数.

出行者选择高速公路或者普通道路出行,主要是出于收费价格及时间长短的考虑,这两个因素起到了决定性作用,基于此建立下层规划中的广义费用函数,即

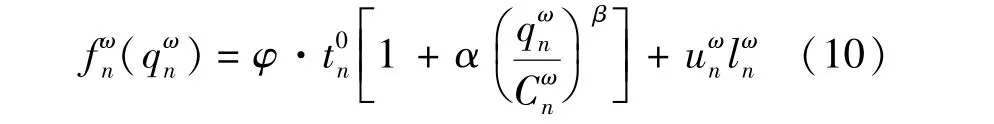
式中 φ表示时间与费用的转换系数;t0n表示路段上流量为零时一辆车自由行使所需时间;α、β为BPR函数的系数,通常取值为0.15和4.0.

其中,φ即为地区平均时间价值,可由式(11)得出:

2.4 算法设计

双层规划是一个NP-hard问题,不存在多项式求解算法,即使能找到问题的解,通常也只能是一个局部最优解而非全局最优解.本文采用模拟退火算法求解双层规划模型.

模拟退火算法来源于固体退火原理,将固体加温至充分高,再让其徐徐冷却,加温时,固体内部粒子随温度升高变为无序状,内能增大,而徐徐冷却时粒子渐趋有序,在每个温度都达到平衡态,最后在常温时达到基态,内能减为最小.该算法采用了Metropolis准则的领域移动方法,这种移动方法保证了算法具有跳出局部最小和趋向全局最优的能力,其实质是依据一定的概率来决定当前解是否向新解移动.其具体步骤如下:

第1步上层规划无约束化,采用非可微精确罚函数处理约束.根据惩罚函数法,将约束最优化问题转化为增广目标函数极小值问题.

minF(uωn,Lk)=min{f(uωn)+Lk·P(uωn)} (12)

式中 {Lk}是一单调增加正序列;f()表示不加惩罚项的目标函数;P()表示惩罚函数.

第2步初始化.设定高速公路的收费费率的初始解,将代入下层规划进行求解,得到,将代入上层规划,计算得.令.设定内层循环次数m,常数h,步长初始值ξ,给定的初始温度T0和终止温度Tf,令外层循环次数n=0,Tn=T0.

第3步对温度Tn,进行如下步骤:

(1)内层循环次数k=1;

(5)若k=m,转第4步;否则k=k+1,转第3步的(2).

第4步判断是否终止.若Tn＜Tf,则令x= uh,即所求高速公路收费费率;否则令ξ=ξ,同时根据Tk+1=Tk·r(其中r∈(0.95, 0.99))进行降温降低Tn,转到第二步.

3 实例分析

梅观高速是深圳市中部南北方向的主干道,南连皇岗口岸,北接莞深高速,是深圳与东莞两地主要的交通要道,也是香港与中国内地货物运输的主要陆路通道之一.梅坂大道—五和大道—观澜大道是与梅观高速平行线位的地方道路,也是深圳市民前往观澜、东莞等地的主要道路之一.

3.1 数据准备

梅观高速全长19.189 km,设计速度100 km/h,全线双向6车道,据最新数据显示,交通流量达到6 136 pcu/h(其中折算系数采用交通部2004年1月发布的《公路工程技术标准》JTG B01-2003规定),通行能力达12 000 pcu/h,现实行收费标准为0.6元/(pcu·km).

梅坂大道—五和大道—观澜大道全长29.3 km,设计速度60 km/h,全线双向6车道,交通流量约为5 000 pcu/h,通行能力达7 200 pcu/h,普通道路全程不收费.

根据深圳与东莞两地最新统计数据,并考虑出行者对时间价值的敏感性,计算得平均时间价值为36.2元/h.

3.2 测算结果

根据上述公式及数据,分别计算得高速公路与普通公路的广义费用函数(其中为简化算式,车流量单位为万pcu/h为:

根据上述模型及算法,初始温度T0=100,结束温度Tf=0.01,常数h=2,步长ξ=0.25,内层循环m=5,因考虑收费费率运用Excel软件进行编程迭代50次,当u≤0.143时,普通公路的车流量将低于10%,为499辆,根据假设条件4,过低的普通道路流量不符合交通管理者的初衷,并考虑收费方便性,收费费率保留两位小数.因此根据运算结果,建议高速公路收费费率为0.15≤u≤0.2,计算结果如表1所示.

表1 部分计算结果表Table 1 Table of part of the calculation results table

根据计算结果,建议该高速公路收费费率取0.15元/(pcu·km),路费收入可达26 735万元,而同时依据梅观高速实际情况以及参数标定方法, K日=2,K车道=1.04,X1=17,X2=243 720,X3= 0,X4=0,X5=1,K固定=128,预测年份为2013年,并考虑大修费用分担到日常年份,根据计算年度养护成本为18 105万元.管理费用根据梅观高速实际年均管理费用3 113万元,因此全年养护成本及管理费用支出为21 218万元.

路费收入高于养护及管理费用支出,符合要求.

4 研究结论

本文从交通管理者角度出发研究高速公路收费到期或政府回购后的养护及管理成本的解决方法,提出以大幅降低收费标准继续收费的方式维持高速公路的高效、通畅、舒适和安全.本文以路网延误时间为上层规划目标函数,以各交通方式广义出行费用为下层规划,充分考虑实际情况,得出适合实际的高速公路收费费率0.15元/ (pcu·km).

其中计算结果路费收入远高于养护及管理费用,但考虑到该高速公路为深圳主要南北通道,车流量高于深圳乃至全国高速公路平均水平,多余收入可由交通管理部门补贴区域内管养费用不足路段以及改善普通公路道路环境.

本文未来研究方向可归纳为以下几点:

(1)本文采用实例为东部发达地区案例,车流量较其它地区高,所得路费收入远高于养护及管理成本支出.后续研究可以根据地区不同制定不同的收费费率,以满足不同地区需要,同时多余路费收入可考虑用于提升地方道路等级或其它路网建设管理支出.

(2)本文收费费率相对较低,同时导致高速公路车流量较多.后续研究可以从收费站通过能力出发,研究统一使用ETC系统、取消收费站采用年费或油税等形式,一方面减少了缴纳低额路费的不便,另一方面也解决了车流通过收费站的瓶颈问题.

(3)本文高速公路不考虑级差效应,仅实现养护及管理成本的自给,使得交通管理者有充足的条件调节路网交通量.后续研究可以从微利模式、低碳模式、不收费模式等方向研究高速公路收费费率问题.

[1] 龙涌,蒋葛夫,冯云才.高速公路收费标准制定方法探讨[J].西南交通大学学报,2001,36(4):421-424. [LONG Y,JIANG G F,FENG Y C.An exploratory study on measures to formulate freeway's toll standard [J].Journal of Southwest Jiaotong University,2011,36 (4):421-424.]

[2] 李扬.高速公路最佳收费标准的测算研究[J].公路, 2003(5):99-102.[LI Y.Reasearch on inference of optimal toll standard for expressway[J].Highway,2003 (5):99-102.]

[3] 张丽洁.特大城市高速公路城区段收费模型[J].交通与运输(学术版),2012,1(1):115-117.[ZHANG L J.Toll model of urban expressway in mega-cities[J]. Traffic and Transportation.2012,1(1):115-117.]

[4] 徐淑雨.高速公路通行费费率的优化模型研究[D].北京交通大学硕士学位论文,2006.[XU S Y.Research on optimization model of expressway toll rates[D].Master Thesis of Beijing Jiaotong University,2006.]

[5] 李冬梅.高速公路拥挤收费费率研究[D].东南大学硕士学位论文,2004.[LI D M.Research on the congestion pricing of freeway[D].Master Thesis of Southeast University,2004.]

[6] 王盛.基于双层规划的公路收费均衡配流模型研究[J].交通运输系统工程与信息,2004,4(1):68-75.[ WANG S.Road tolling UE method based on Bi-level programming model[J].JournalofTransportation Systems Engineering and Information Technology,2004, 4(1):68-75.]

[7] 刘万里,孟祥茹.高速公路运营管理[M].机械工业出版社,2004.[LIU W L,MENG X R.Highway operationandmanagement[M].ChinaMachine Press,2004.]

Research on Highway Toll Rates Based on the Cost of Conservation

LIN Wen-xin1,2,WANG Jian-wei1,LIN Yu-Jun2
(1.College of Economy and Management,Chang'an University,Xi'an 710064,China; 2.Shenzhen Expressway Company Limited,Shenzhen 518026,Guangdong,China)

Highway would face problems such as traffic congestion and maintenance cost rise of road infrastructure after highway toll phase expires or government repurchases.Toll extension but at a lower rate out of road conservation purpose is considered to be one feasible approach to mitigate the financial burdens and dissolve the social media pressure.From this point of view,a bilevel programming model is built.On the upper level,road network manager(government)as the leader maximizes the network traffic load and minimizes the total network delay;the lower bound of charging which ensures the reasonable profits and maintenance costs of network operator,as well as the upper bound of charging determined by the road users affordability is also considered.On the lower level,User Equilibrium(UE)model is built in full account of route choice heterogeneity and the congestion effect on traffic demand distribution.Simulated Annealing (SA)is used to validate the model and find the reference toll rate.

highway transportation;toll rate;bi-level programming model;maintenance costs;simulated annealing algorithm

U4-9

: A

U4-9

A

1009-6744(2013)05-0145-05

2013-04-25

2013-06-09录用日期:2013-06-25

教育部人文社会科学研究青年基金项目(12YJCZH051).

林文新(1978-),男,福建邵武人,博士生.

*通讯作者:wjianwei@chd.edu.cn