带立即折返的高速动车组乘务交路回路优化编制方法
杨嘉宝,符卓
带立即折返的高速动车组乘务交路回路优化编制方法
杨嘉宝,符卓
(中南大学 交通运输工程学院,湖南 长沙 410075)
机车乘务交路回路是机车乘务交路的组成部分,其合理构建对于乘务人员(司机)的劳动效率和铁路运输的成本具有重要意义。通过对带立即折返的高速动车组乘务交路回路优化构建问题的分析和抽象,根据其问题特点在已有的集合分解问题(set partitioning problem)模型基础上进行拓展,建立其优化模型,并设计一个蚁群-遗传混合算法求解该模型。研究结果表明:用该方法求出的乘务交路回路方案优于铁路现场现行的“先到先走”的方法。
铁路运输;机车乘务交路;立即折返;集合分解问题;蚁群−遗传混合算法
铁路机车(含动车组)运用工作主要由3部分组成:机车交路编制、机车乘务交路编制和机车乘务排班计划编制(把乘务交路分配给乘务员(司机))。机车交路是机车乘务交路编制的基础,而机车乘务交路则是机车乘务排班计划编制的基础。机车乘务交路合理与否,直接关系到所需要的乘务员(司机)数量及其乘务员的劳动生产率。对于机车乘务交路的编制,我国铁路部门目前仍然靠人工凭经验来进行,编制质量和效率都有待于借助科学的方法和手段来提高。铁路机车乘务交路编制可划分为3个阶段:确定乘务片段、编制乘务交路回路、编制乘务交路循环。乘务片段是指在乘务区段值乘的“一个单程或立折交路”(乘务组在退勤休息或间休前连续值乘的交路)。乘务交路回路(简称乘务回路)由固定搭配值乘的1对乘务片段组成。乘务交路循环(简称乘务循环)则由一个固定周期内轮流值乘的多个乘务回路连接组成。目前,我国铁路机车和高速动车组的运用和乘务工作组织采用的是长交路、轮乘制。普速机车乘务回路基本上是由1对往返的乘务片段组成。但对于高速动车组乘务回路的构建,由于交路区段划分、列车运行速度、乘务作息时间等方面的不同,其乘务片段中除了与普速机车类似的非立即折返类型外,还存在大量的立即折返类型。非立即折返的高速动车组乘务回路编制,与普速机车乘务回路的编制基本相同,按铁路现场现行的“先到先走”原则编制即可。但带立即折返的高速动车组乘务回路编制却不同,按“先到先走”的方法编制出来的,往往不是最优方案,即构成乘务回路的乘务片段间总接续时间不是最短的,导致所需乘务员数不是最少的。乘务交路计划编制问题,广泛存在于铁路[1−2]、航空[3−4]及城市公交[5−6]等领域,其中我国铁路运输中的乘务交路计划研究近年来取得一些成果。在已有文献中,乘务交路计划编制问题主要归结为2种模型[7]:集合覆盖(set covering)和集合分解(set partitioning,也称集合划分)。在铁路乘务交路计划问题中,2种问题模型的目标函数一致,主要区别在于是否存在乘务员便乘这一条件。赵鹏等[8]将机车乘务员运用计划优化编制归结为集合覆盖或分解问题。但由于当时我国高铁处于起步阶段,该研究仅模拟了京沪高铁长距离条件下的乘务交路计划。田志强[9]针对乘务员便乘情况,将乘务员的值乘时间转化为费用,以总费用最小为目标采用集合覆盖模型对可行乘务交路段费用进行计算,其中的时间成本恰好为集合覆盖模型中的权值,构建带权值的集合覆盖模型。部分学者研究了乘务排班计划问题[10−11],并提出了相应的模型和算法。带立即折返的乘务交路回路编制问题属乘务回路构建的一种,随着我国高铁的不断发展,立即折返乘务交路也日益增多。本文在已有研究的基础上主要研究带立即折返的高速动车组乘务交路回路优化编制问题,针对该问题的特殊性,参考集合分解模型进行拓展,并设计求解算法,最后通过对实例的求解和对比分析,验证所提出方法的效果。
1 问题描述
高速动车组乘务回路构建可分为3种类型:
1) 间休折返型。指乘务员从机务本段站出勤值乘去程乘务片段,到达折返站后按规定间休,再值乘一返程乘务片段返回机务本段站,也称非立即折返。该类型的乘务回路构建,与普速机车乘务回路构建本质相同,只是乘务片段和间休的时间长短略有差异,如图1所示,图1中的P表示乘务片段。

图1 间休折返
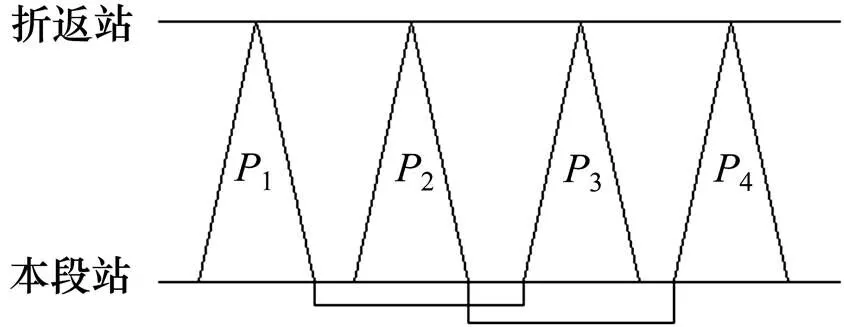
图2 纯立即折返
2) 纯立即折返型。指乘务员从机务本段站出勤值乘,到达折返站后,在停留时间大于最小立折接续时间、小于90 min,且往返总旅行时间(含立折接续时间)不超过4 h的情况下,立即值乘另一车次(一般为同一动车组)返回机务本段站,形成一个由乘务子回路组成的立折乘务片段,间休后再值乘另一立折乘务片段,再次返回机务本段站,然后退勤,形成带立折的乘务回路,如图2所示。与间休折返型不同,此情形下的乘务片段不分去、返程,即每个立折乘务片段既可被其他立折乘务片段接续,也可接续其他立折乘务片段。
3) 混合折返型。由立折乘务片段和非立折乘务片段混合组成,即从机务本段站(或折返站)出发,值乘“去程”乘务片段,按规定间休后,再值乘一“返程”乘务片段到达折返站(本段站)终止的“回路”,如图3所示,其中P表示立折乘务片段,Q表示从折返站返回的非立折片段,R表示从本段站出发的非立折片段。

图3 混合折返
因立折乘务片段在起点站同时有起始时刻和终止时刻,使得在构建带立折的乘务回路时,需对每个立折乘务片段确定其是接续其他乘务片段,还是被其他乘务片段接续,所以带立折的高速动车组乘务回路的构建比间休折返型要复杂。该问题是我国开行高速动车组后,在机车乘务组织方面出现的新问题,但目前文献中尚未见到解决此问题的相关报道。而铁路现场工作中基本参照间休折返型,先采用“先到先走”的方式构建带立折的乘务回路,再根据情况,由人工凭经验进行局部调整。
在构建带立折的高速动车组乘务回路时,由于列车到发点的原因,会出现2种情形:其一是所有乘务片段都能相互配对构成乘务回路;其二是有部分乘务片段相互间不能配对构成乘务回路,而只能单独值乘,成为单乘务片段“回路”。本文将只针对第一种情形进行研究,第二种情形将另文讨论。
2 优化模型
2.1 构建带立折的乘务回路接续时间矩阵
带立折的乘务片段的特殊点在于在本段同时有起始时刻与终止时刻,乘务组从本段出发到达折返段并立即返回本段这一个过程可视为一个立折乘务片段,且这种立折乘务片段在满足时间空间约束条件下,每个立折片段可以接续或被接续另一个立折或非立折片段,且有多种接续组合,因此接续时间也有所差异。
高速动车组的乘务交路以0点为界划分每一天,通过给定的0~24点高速动车组运行时刻表,可建立乘务片段接续时间表。需注意的是:根据规定,高速动车组司机值乘2个乘务片段之间的休息时间(间休时间)不小于90 min,可将其称为最短接续时间。当2个不同的乘务片段之间的接续时间小于此最短接续时间或需跨天配对时,则视为无效接续。纯立折乘务片段的接续时间为表1中前行、列所组成的(×)阶子矩阵;混合型乘务片段的接续时间矩阵为表1中(+)×(+)阶矩阵。
经过“ICME-14申办委员会”2013年3月—2014年10月紧张的申办准备工作,2014年11月30日正式递交申办书.

表1 接续时间矩阵
表1中,P(=1,…,)表示立折乘务片段;Q(=+1,…,)表示从折返站返回的非立折乘务片段;R(=+1,…,)表示从本站出发的非立折乘务片段。令=为乘务片段总数目,则C(=1,…,)表示值乘乘务片段P(或Q,R)后接着值乘乘务片段P(或Q,R)的接续时间;无效接续情况下相应的乘务片段不能接续,对应的元素用一个足够大的正整数表示。
2.2 带立折乘务回路构建的转化
通过分析,发现带立即折返乘务片段的乘务回路优化构建问题与集合分解问题很强的关联性。主要异同点可归纳如下:
1) 对于所有乘务片段,可视为一个有限集集合,而乘务片段间组成的可行乘务回路就可作为这个有限集的子集族,且这些可行乘务回路完全覆盖所有乘务片段。在所有可行乘务回路中,都存在一个接续时间,即一般集合分解问题中的权值,因此问题可表述为:在包含所有可行乘务回路的集合中寻求一组子回路集,在满足完全覆盖所有立折和非立折乘务片段的情况下,使得回路总接续时间最短,即总权值最小。
2) 一般的集合分解问题中,子集族元素的组合是多样的,一个小子集可包含元素数目也不确定。而带立即折返乘务交路回路构建问题中,乘务片段之间要满足相关乘务规则,因而每个立折乘务片段最多上只能与另一立折(或非立折)乘务片段构成一个回路,即可基本满足1 d的值乘工作量。
3) 在一般的集合分解问题中,每两个元素组合后均有一个权值,且不受元素间组合的顺序影响,例如:{1,3}与{3,1}2个集合的权值是同一个值。但在带立即折返的高速动车乘务交路回路构建问题中,两乘务片段组合的顺序不同,接续时间也有所不同,即权值不同。
4) 带立即折返的乘务回路构建问题中,一旦某立折(非立折)片段被选中与另一个立折(非立折)片段组成乘务回路,其他乘务片段则无法再与之进行组合,即集合分解问题中的元素只能无重复覆盖一次。
2.3 优化目标和约束条件
求解带立即折返的高速动车组乘务交路回路问题的优化目标:乘务片段两两相互组合形成的乘务回路总接续时间最短,即使乘务员无效的等待时间为最少,从而减少乘务员需要数。
在乘务片段相互接续组合时,需满足以下几个条件:
1) 每个乘务片段都被包含在最终解中,且在解中仅出现一次。
2) 每2个乘务片段接续后,其接续时间与接续顺序相关。
3) 当任意一个乘务片段与另一乘务片段认定接续后,其他任何未接续的乘务片段均无法再与已认定接续的乘务片段进行接续。
4) 在带立即折返乘务回路构建问题中,需满足相应的乘务休息时间标准。
2.4 数学模型
Gershkoff[12]、田志强[9]和陈海平[7]均曾在论文中提到基于可行乘务回路建立的集合分解模型 如下:


式中:x为0~1变量,当x=1时表示可行乘务回路被选入最优解,x=0时表示未入选;c为可行乘务回路的费用;a为0~1变量,a=1时表示可行乘务回路覆盖乘务区段,a=0时表示未覆盖。
式(1)表示模型目标函数为求解时间费用最小的乘务回路,式(2)表示每个乘务区段只能被覆盖一次。
根据以上模型及本文2.2中求解带立即折返的高速动车组乘务回路问题的优化目标和约束条件,可建立其模型如下:

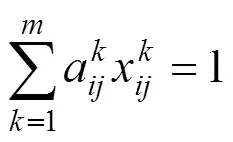


=1,2,…,;1,2,…,(7)

1,2,…,;=1,2,…,(8)

式(3)表示求解接续时间最短的乘务回路;
式(4)表示每个乘务片段只能被一个存在于解集合中的可行回路所覆盖;
式(5)表示解集合中,组合前后顺序不同的2个立折或非立折乘务片段只能出现一次,且2个认定接续的乘务片段将无法接续其他乘务片段;
式(6)表示当和2个乘务片段进行组合时,若同一天内的接续时间小于规定的最短接续时间或跨天接续,则用一个足够大的整数表示,以说明2个乘务片段不能接续。
对比2个模型,本文所构建的模型中主要增加式(5)和式(6)2个约束条件,可以看作是原集合分解模型的拓展。该拓展模型中由于立折片段可接续或被接续其他乘务片段,接续时需考虑顺序问题。针对立折问题中存在已接续的2个乘务片段都不能接续其他乘务片段且不能改变自身的接续顺序这一限制因素,可通过式(5)表示。
3 求解模型的蚁群−遗传混合算法
集合分解问题已被证明为NP难问题[13]。根据上述分析,带立即折返的高速动车组乘务回路优化问题中的模型是在已有集合分解模型上进行的拓展,显然,也为NP难问题,且实际乘务回路构建问题规模较大,需采用启发式算法求解。蚁群算法具有较强的随机性和正反馈作用,常用来解决路径最优问题,但易陷入局部最优。遗传算法实行并行搜索,交叉、变异操作能保持种群的多样性,全局搜索能力较强,但收敛速度较慢。所以可利用蚁群算法提供较好的初始解,有利于加快遗传算法的收敛,再通过交叉、变异操作可有效避免蚁群算法易陷入局部最优解的弊端。因此,本文设计蚁群-遗传混合算法对带立即折返的高速动车组机车乘务回路优化问题进行求解。
3.1 算法描述
根据蚁群算法和遗传算法的特点,以及带立折的乘务回路构建问题的实际情况,先利用蚁群算法在解空间随机安置只蚂蚁对可行解进行搜索,完成迭代后,选取部分较优解作为遗传算法的初始种群,进行遗传操作,最终得出近优解或最优解。
3.2 算法步骤
在算法中规定有只蚂蚁随机对2个元素进行搜索,并将蚂蚁走过的元素及位置存放在周游表()表中,可供选择的元素及位置存放在()表中(=1,2,…,),迭代次数为。


蚁群算法中蚂蚁在其行走路径上的信息素浓度也会逐渐消失,设参数(0<<1)表示信息素挥发程度。因此在所有蚂蚁完成一次循环后,其路径上的信息素浓度需实时更新[14],即:
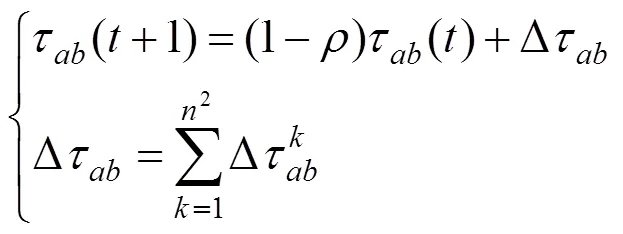

算法具体步骤如下:
Step 1:初始化,,和等各项参数;
Step 2:将只蚂蚁随机放置在接续时间矩阵中的元素上;
Step 3:记录每只蚂蚁的初始位置,即元素在表中的坐标,存放在()表中;
Step 4:从第只蚂蚁开始,根据概率的大小,从()表中选择下一元素,将被选元素记录在()表中,同时在()表中删除将含有被选元素坐标的元素;
Step 5:判断蚂蚁是否使()表中元素为空,否,则返回Step 3;
Step 6:对蚂蚁走过的元素的值进行求和,并记录,更新信息素浓度及路径信息;
Step 7:判断迭代次数是否超过规定次数,否,执行Step 2至Step 6;
Step 8:当=时,得到每只蚂蚁的序列,取前个较优解作为遗传算法的初始种群;
Step 9:计算适应度;
Step 10:进行遗传操作;
Step 11:输出最终解。
4 算例分析
本文采用南昌机务段值乘的南昌-九江乘务区段的相关数据,对模型和算法进行验证。基础数据见表2。

表2 带立即折返的高速动车组列车时刻表
根据立折返高速动车组列车时刻表数据及规定的最小接续时间,构造乘务片段接续时间矩阵如表3所示,其中,的值设置为109。
蚁群算法部分参数见表4,遗传算法部分参数见表5。
该蚁群−遗传混合算法已用Matlab语言编程实现,在Intel Core5 CPU2.7GHz、内存4GB的计算机上运行40.140 4 s,得到本算例的乘务回路数为9个,即每天需派出9位乘务员值乘,总接续时间为2 658 min,且具有多种交路回路构建方案,任选其中一个方案为:2-5,3-18,4-11,9-12,10-1,13-7,15-8,16-6和17-14。若采用铁路现场目前常用的“先到先走”原则构建,得到的方案为:16-6,3-17,2-5,13-7,4-8,15-9,10-1,11,12,14和18,即每天需派出11位乘务员值乘,比用本文提出的优化算法求出的方案多2位。原因是按“先到先走”顺序排下来,最后剩下的11,12,14和18号乘务片段相互间无法配对构成回路,只能分别单独构成只包含一个乘务片段的乘务“回路”。优化后的方案使工作时间更加紧凑,缩短了乘务员的工作冗余时间,从而减少了乘务员需要数。
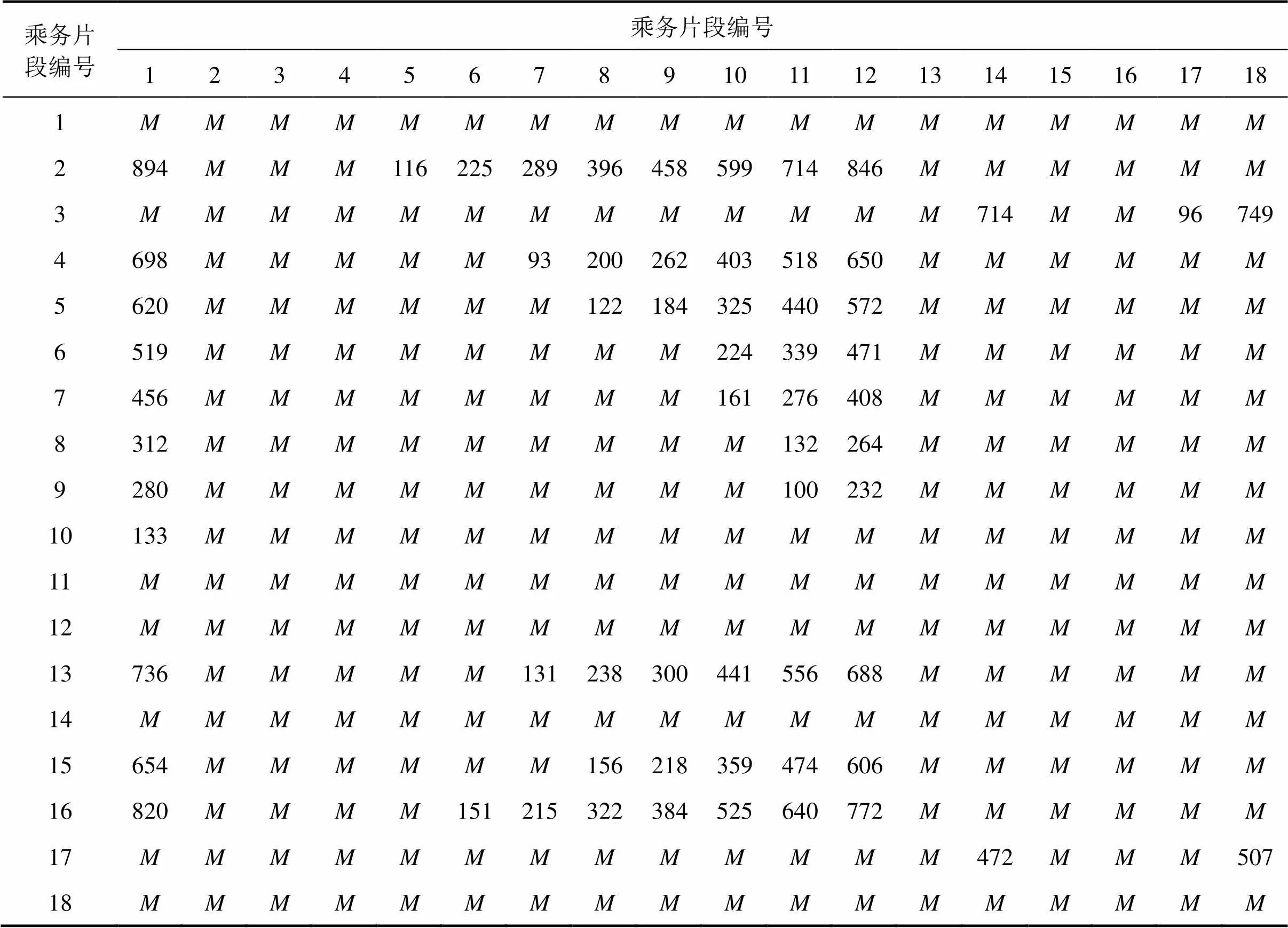
表3 带立即折返的乘务片段接续时间矩阵

表4 蚁群算法参数

表5 遗传算法参数
5 结论
1) 带立即折返的高速动车组乘务回路编制问题,是我国开行高速动车组后在司机乘务组织方面出现的新问题。此时用现场常用的“先到先走”的传统方法编制出来的乘务交路方案,往往不是最优方案。
2) 本文根据带立即折返的高速动车组乘务回路编制问题的特点,针对所有乘务片段都能相互配对构成乘务回路的情形,在集合分解模型基础上建立了该问题的数学模型,并设计了求解的蚁群−遗传混合算法。经实例求解和对比分析,优化方案相比按“先到先走”编制出来的方案,使乘务员的工作时间更加紧凑,节约了乘务员的需要数,验证了该方法的有效性和合理性。
[1] 黄珊. 机车乘务员运用问题及其辅助编排系统研究[D].长沙: 中南大学, 2014. HUANG Shan. Locomotive crew scheduling problem and scheduling assistant system[D]. Changsha: Central South University, 2014.
[2] 杨国元, 史天运, 张秋亮. 铁路客运乘务排班计划编制模型及算法[J]. 交通运输系统工程与信息, 2016, 16(4): 159−164. YANG Guoyuan, SHI Tianyun, ZHANG Qiuliang. Model and algorithm for railway passenger crew rostering plan[J]. Journal of Transportation System Engineering and Information Technology, 2016, 16(4): 159−164.
[3] Lavoie S, Minoux M, Odier E. A new approach of crew pairing problems by column generation and application to air transport[J]. European Journal of Operational Research, 1988(35): 45−58.
[4] Balaji Gopalakrishnan, Ellis L Johnson. Airline crew scheduling: State-of-the-art[J]. Annals of Operations Research, 2005, 140(1): 305−337.
[5] Desrochers M, Soumis F. A column generation approach to the urban transit crewing scheduling problem[J]. Transportation Science, 1989, 23(1): 1−14.
[6] Chu S C K, Chan E C H. Crew scheduling of light rail transit in Hongkong: from modeling to impelmentation[J]. Computer Ops Res, 1998, 25(11): 887−894.
[7] 陈海平. 高速铁路乘务组织理论与优化研究[D]. 北京: 北京交通大学, 2013. CHEN Haiping. Research on theory and optimization of crew organization of high-speed railway[D]. Beijing: Beijing Jiaotong University, 2013.
[8] 赵鹏, 胡安洲, 杨浩. 机车乘务员运用计划的优化编制[J]. 铁道学报, 1998, 20(4): 8−13.ZHAO Peng, HU Anzhou, YANG Hao. Research on optimization of crew scheduling[J]. Journal of the China Railway Society, 1998, 20(4): 8−13.
[9] 田志强. 高速铁路乘务计划编制优化理论与方法研究[D]. 成都: 西南交通大学, 2011.TIAN Zhiqiang. Study on theory and methods of crew planning problem of high-speed railway[D]. Chengdu: Southwest Jiaotong University, 2011.
[10] 黎符忠, 王文宪, 陈皓. 混合遗传算法在客运专线司机乘务排班中的应用[J]. 铁道运输与经济, 2015, 37(8): 88−92. LI Fuzhong, WANG Wenxian, CHEN Hao. Application of hybrid genetic algorithm on DPL driver crew scheduling[J]. Railway Transport and Economy, 2015, 37(8): 88−92.
[11] 王兴慧, 颉俊杰. 基于均衡性的机车乘务排班计划编制方法研究[J]. 交通科技与经济, 2015, 17(5): 55−59.WANG Xinghui, XIE Junjie. Research on the crew rostering plan of trainset based on equilibrium[J]. Technology & Economy in Areas of Communications, 2015, 17(5): 55−59.
[12] Gershkoff I.Optimizing flight crew schedules[J]. Interfaces, 1989, 19(4): 29−43.
[13] Garey M R, Johnson D S. Computers and intractability: a guide to the theory of NP-completeness[M]. San Francisco: W. H. Freeman, 1979: 23−26.
[14] 史峰, 王辉. Matlab智能算法30个案例分析[M]. 北京:北京航空航天大学出版社, 2011.SHI Feng, WANG Hui. Analysis of 30 cases of Matlab algorithm[M]. Beijing: Beihang University Press, 2011.
An optimization method for high-speed motor train unit crew roundtrip routing problem with immediate turn-back
YANG Jiabao, FU Zhuo
(School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China)
The locomotive crew roundtrip routing is a part of the locomotive crew planning problem, and its reasonable construction is of great significance to the labor capacity of the crew (driver) and the cost of the railway transportation. In this paper, the high-speed motor train unit crew roundtrip routing problem with immediate turn-back is analyzed and abstracted. According to its characteristics,based on the model of set partitioning problem, an optimization model for it is established. A hybrid ant colony genetic algorithm is designed to solve the model. Computational results on real data show that the plan by this method is better than the “first come, first left” scheme.
railway transportation; immediate turn-back; locomotive crew routing; set partitioning problem; hybrid ant colony genetic algorithm
10.19713/j.cnki.43−1423/u.2018.11.003
U292
A
1672 − 7029(2018)11 − 2738 − 08
2017−11−07
国家自然科学基金资助项目(71271220);南昌铁路局科技研究开发计划资助项目(201713)
符卓(1960−),男,海南文昌人,教授,博士,从事交通运输规划与管理研究;E−mail:zhfu@csu.edu.cn
(编辑 蒋学东)

