对共顶点椭圆(圆)与双曲线的辩证认知
☉江苏省海门市包场高级中学 钱 斌
解析几何中有一些问题是比较独特的,比如圆系知识必需是在两圆有交点的前提下才能运用,否则圆系是没有意义的;共顶点的椭圆、双曲线和抛物线恰好存在着实虚根之间的巧妙转化,笔者对这些虚虚实实、实实虚虚的问题做过一些探究,现将此整理成文请读者一起来化虚为实,探索虚根的含义.
一、圆与双曲线的辩证认识——两圆无交点时的圆系
例1(人教A版数学必修2习题A组第10题)求经过两圆x2+y2+6x-4=0和x2+y2+6y-28=0的交点,并且圆心在直线x-y-4=0上的圆方程.

变式: 求经过两圆C1:x2+y2=1,C2:(x-4)2+y2=1的交点,并过(0,0)点的圆方程.(注意:此两圆是无交点的)
误解:设所求圆方程为:
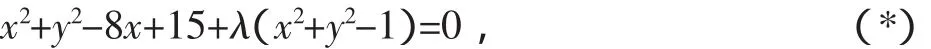



图1
总结:经过笔者验证,发现两圆内含时,也存在上述现象.通过上述分析,当两圆无交点时(相离、内含),此时圆系方程不能表示实体圆存在,但此时共顶点双曲线系方程必过此(虚)交点,从复数范围来说,代数方法将虚和实统一在二元二次方程中了!笔者将上述现象称为虚圆系.因此,笔者总结了下列定理(虚圆系定理):

二、椭圆与双曲线的辩证认识——对一个离心率问题的探索

解析:这是非常普通的一道离心率定值问题,但其背后隐藏着对圆锥曲线辩证统一的认知.先看两个解法:

图2

分析:很明显,解法2是错误的!因为x1x2=-a2可知两根异号,但实际图中两根均为正根,所以解法2是错误的.对于这类问题,很多教师都是用几何法处理的,但有些学生选择的是代数法,教师该如何阐释缘由呢?为了解释清晰,笔者先引入一个定义和引理.
引理:实系数方程ax2+bx+c=0与ax2-bx+c=0的根互为相反数.
证明:(1)a=0时,引理显然成立;
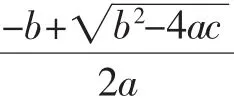


图3
(1)双曲线与抛物线的交点.


(2)椭圆与抛物线的交点.
综合上述(1)和(2),对“共顶点椭圆双曲线”来说,它们与抛物线y2=2px(p>0)的交点恰好是实根与虚根的互换.
辨析:现在可以解释为什么例2的解法2是错误的:

三、系统高度辩证认知
(1)从学生的角度而言,笔者认为学生的思维往往比较直接,给什么做什么是大部分学生解决数学问题的基调.以本文第2个问题而言,有些学生解决本题的思维倾向于代数方式,采用联立方程和韦达定理,殊不知二元二次方程中虚根的存在,在问题的背后深深隐藏着学生对“以数解形”完备性认知的缺乏,同时也让学生深刻理解“以数解形”在这样问题中的优越性,值得教师教学多加渗透和予以关注.
(2)从教师的角度而言,这样的问题有利于开拓学生的视野和培养其创新的思维,值得在这样的探究性问题上多下功夫,平时教学中,笔者觉得“以形辅数”(几何法,使用相对较多)很轻快、较简洁、便于教学,但是不足之处在于只能就题论题;而“以数解形”(代数法)往往站在了系统的高度,很完美、较复杂、但散发出问题的本质;传授知识时,我们应该毫无疑问的多选择几何法,但对于自身优秀的学生而言,也要注重“以数解形”对圆锥曲线是一个统一体的本质理解!
(3)笔者想起人教A版中圆锥曲线的章头图,何为“圆锥曲线”呢?当然是用一个截面截圆锥而成的!通过特定角度切割圆锥体表面得到圆、椭圆、抛物线、双曲线这四种曲线.其实用统一的眼光来看,它们本身是一个整体.其差别在于用截面的角度带来了圆锥曲线离心率的不同,但是e>1和0≤e<1之间有着完美的对称.用统一的代数语言——方程Ax2+By2+Cxy+Dx+Ey+F=0就是对他们最完美的诠释!
(4)从思想方法的角度而言,圆锥曲线问题渗透出的主要数学思想方法便是数形结合思想.有时形优于数,有时则恰恰相反,这需要教师通过各种问题对学生进行经验的积累.
将文中的例1用二次曲线系阐述:过两圆锥曲线A1x2+B1y2+C1xy+D1x+E1y+F1=0和A2x2+B2y2+C2xy+D2x+E2y+F2=0交点的曲线系方程,设为:A1x2+B1y2+C1xy+D1x+E1y+F1+λ(A2x2+B2y2+C2xy+D2x+E2y+F2)=0,这样我们就站在系统的高度认识了圆系!其实圆系就是二次曲线系的一种特殊情形.双曲线系也在其中,文中的虚圆系正是如此!难怪,两圆无交点,圆系也能求解了!通过文中的两个问题的探索,多方联系,浑然一体,虚实结合,妙探虚知!

