圆锥曲线统一定义的探索历程

☉江苏省连云港市新浦中学 李 萌

新课标人教A版《数学》选修教材2-1中只介绍了椭圆、双曲线、抛物线的第一定义，也就是说学生只知道抛物线准线的概念及准线方程，而不知道椭圆、双曲线准线的概念及其准线方程.但近年来无论是各地市的调研题、模拟题，还是全国高考题在解析几何考题上都或多或少的涉及到与椭圆、双曲线的准线相关的问题.面对这种情形，我们大多数一线教师（包括笔者）的做法就是将圆锥曲线统一定义强行推销给学生，并通过大量习题的练习强化巩固，这样的做法一方面违背了新课程理念，新课程在圆锥曲线章节中删去了圆锥曲线的统一定义，而我们又毫不保留的推销给学生并通过重复习题的练习强化、深化，无疑加重了学生学习的负担；另一方面，由于学生接受新知识，形成新概念需要有一个经历的过程，直接的推销等于把新知识灌输给学生，那么学生真的懂了吗？真的接受了吗？回首展望，冷静反思，留给学生更多的是这个定义怎么来的？

基于上述原因，笔者进行仔细斟酌、认真的思考研究，认为应从椭圆、双曲线的第一定义出发引导学生来探索圆锥曲线的统一定义，或者从抛物线的定义出发来探索圆锥曲线的统一定义更加切合学生思维的最近发展区，消除学生之前的种种疑惑.

一、从椭圆、双曲线的定义出发去探索圆锥曲线的统一定义

1.从椭圆的第一定义出发探索椭圆的第二定义

如何从上述定义中找出椭圆的准线，探索出椭圆的第二定义呢？我们可以引导学生从建立椭圆方程开始.

设M（x，y）是椭圆上任意一点，椭圆的焦距为2c（c＞0），那么焦点F1，F2的坐标分别为（-c，0），（c，0）.又设M与F1，F2的距离的和等于2a.由椭圆的定义知a＞c.

由椭圆的定义得方程

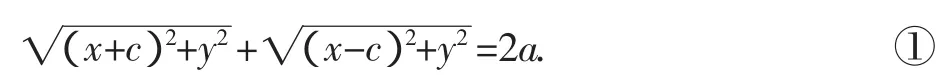
对方程①的左边施行分子有理化得

对上式化简整理得

由①与②联立

由于上面两个方程式是从方程①等价转换来的，所以椭圆的定义等价叙述为：平面内到定点F的距离和它到定直线l（点F不在直线l上）的距离之比是常数e（0＜e＜1）的点的轨迹是椭圆.类比抛物线的定义，点F是焦点，直线l是准线，e是离心率（椭圆的第二定义）.

2.从双曲线的第一定义出发探索双曲线的第二定义

对于双曲线，我们可引导学生类比椭圆的探索方法，将新课标教材A版《数学》选修2-1第52页给出双曲线的定义等价的叙述为：平面内到定点F的距离和它到定直线l（点F不在直线l上）的距离之比是常数e（e＞1）的点的轨迹是双曲线.点F是焦点，直线l是准线，e是离心率（双曲线的第二定义）.

这样，我们结合抛物线的定义及椭圆、双曲线的第二定义，会得到圆锥曲线的统一定义：平面内到定点F的距离和它到定直线l（点F不在直线l上）的距离之比是常数e的点的轨迹是圆锥曲线，其中F是焦点，直线l是准线，e是离心率.（Ⅰ）当0＜e＜1时，圆锥曲线是椭圆；（Ⅱ）当e＞1时，圆锥曲线是双曲线；（Ⅲ）当e=1时，圆锥曲线是抛物线.

二、从抛物线的定义出发来探索圆锥曲线的统一定义

新课标教材A版《数学》选修2-1在第65页给出了抛物线的定义：平面内与一个定点F和一条定直线l（点F不在直线l上）距离相等的点的轨迹叫做抛物线.点F叫做抛物线的焦点，直线l叫做抛物线的准线.

那么，椭圆、双曲线是否也能通过到定点的距离与到定直线的距离之间的关系来定义呢？我们引导学生做如下的探索.

类比抛物线的定义先进行合理猜想：平面内到一个定点F的距离是它到一条定直线l（点F不在直线l上）距离的λ（λ＞0）倍的点的轨迹是圆锥曲线，F叫做焦点，直线l叫做准线.

这个猜想是否成立？需要大家去验证.

验证：为了和抛物线方程的建立相一致，我们取经过点F且垂直于直线l的直线为x轴，垂足为K，并使原点与线段KF的中点重合，建立直角坐标系.

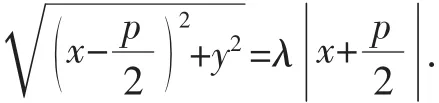
（ⅰ）若λ=1，方程③表示抛物线y2=2px（p＞0）.

（ⅱ）若0＜λ＜1，则方程③可化为

（ⅲ）若λ＞1，则方程③可化为

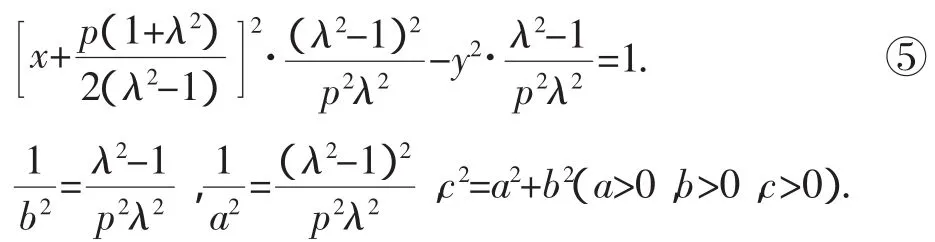
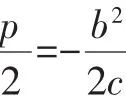
综上可知，猜想成立.于是我们就得到圆锥曲线的统一定义：平面内到定点F的距离和它到定直线l（点F不在直线l上）的距离之比是常数e的点的轨迹是圆锥曲线，其中F是焦点，直线l是准线，e是离心率.（Ⅰ）当0＜e＜1时，圆锥曲线是椭圆；（Ⅱ）当e＞1时，圆锥曲线是双曲线；（Ⅲ）当e=1时，圆锥曲线是抛物线.

三、结语

维果茨基的“最近发展区理论”，认为学生的发展有两种水平：一种是学生的现有水平，另一种是学生可能的发展水平.两者之间的差距就是最近发展区.因此我们的教学，只有针对学生思维的最近发展区的教学，才能促进学生的发展.

圆锥曲线统一定义的探索是在学生已有的圆锥曲线第一定义的知识基础上进行的教学，通过教师的引导，学生的参与探索，使他们零距离的感受到圆锥曲线统一定义的形成不是“无本之木，无源之水”，而是在已有知识的基础上自然形成的，这样的教学能促使学生创新能力的发展，提高学习数学的兴趣.