三角函数扎根“单位圆”
☉江苏省泗洪中学 祖 飞
综观近年各省市高考命题,以单位圆为背景、从三角函数的定义入手成为三角命题新亮点,此类试题,关注三角函数的本质问题,注重考查“过程与方法”,深刻体现了新课标对高考试题的命制要求,下面举例分析.
一、坐标“形化”定义
圆心在原点,半径为1的圆称作单位圆,单位圆的引入使三角函数的定义形象化,单位圆上点的坐标使三角函数值的计算直观明了.


图1
(Ⅰ)求tan(α+β)的值;(Ⅱ)求2α+β的值






点评:角的大小是变化的,由此而成为一个角自变量,角自变量的三角比值、如正弦比值在“角变量”的变化时随之而变,由此正弦值成为“角变量”函数,正弦函数是正弦比值函数的简称.
二、坐标“量化”边长
如果将单位圆视作为动点的轨迹,则此轨迹可看作是:顶点在原点、始边OA=1在x轴正向上,角的终边OP的端点P(x,y)的轨迹,其中x,y分别是端点P的横、纵坐标(如图2).

图2


(Ⅱ)分别过A,B作x轴的垂线,垂足依次为C,D.记△AOC的面积为S1,△BOD的面积为S2.若S1=2S2,求角α的值.

图3



点评:角的概念可从锐角扩展到任意角,此时角的两边与其“所夹的角”虽然不能组成三角形了.但角变量的“三角比”还存在.
三、“同角关系”单位圆的三角式
同角关系中sin2θ+cos2θ=1与单位圆方程x2+y2=1在结构上有本质的联系,在许多情况下可将所要解决的三角问题转化到单位圆中,运用圆的有关知识进行解决,使问题变得直观,常能化繁为简,化难为易,从而达到优化解题的目的.


图4
例4 已知θ为锐角,求满足2cosθ=1+sinθ的θ值.


图5
点评:以上两题,用的是同一种方法,构造单位圆,结合斜率知识解题,简捷而巧妙.在三角问题的求值、求角、证明等过程中,经常会遇到关于sinθ与cosθ的关系式,并且通常使用关系式sin2θ+cos2θ=1进行转化,使问题得到解决.
四、单位圆与三角函数线
数缺形时少直观,形缺数时难入微.单位圆为三角函数值与三角函数线建立的数形结合达到了“直观入微”的境界.


(Ⅱ)求△OPQ面积的最大值.

图6


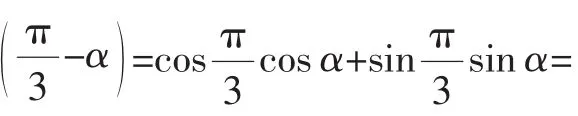
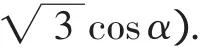


点评:通过单位圆,正弦函数、余弦函数和正切函数的值域、定义域及其单调性也直观可见.微观而隐蔽的三角函数间关系,通过三角函数线可得到简便而直观的解答.
由上面的几个例题,我们可以看出,单位圆视角下命题,不仅体现了课程标准所倡导的“返璞归真,努力揭示数学概念、法则、结论的发展过程和本质”,而且能实现对数学学科知识多维度考查,因此,此类试题必将是试题设计的一个好的始点.

