高中数学探究式教与学的策略

☉江苏省镇江中学 陆建根

在人类的学习活动中，包括两种不同类型的学习方式——“接受性学习”和“探究式学习”.“探究式学习”能让学生经历知识与技能的形成与巩固过程，经历思维的发展过程，经历问题的解决过程，从而将知识、技能、情感内化为生命中的财富.“探究式学习”能使学生的学习欲望得到激发，学习潜力得到拓展，真正成为知识建构的“筑路者”，在积累直接经验、培养创新精神和实践能力等方面有独到之处.探究式学习需要探究式教学的引导，数学课堂采取探究式教学，不仅可以让学生在探究的过程中获取知识形成的体验，更重要的是能为学生解决相关问题提供强有力的支撑，触类旁通，举一反三，并对后续发展产生影响.笔者依托自己的教学实践，对高中数学探究式教与学进行了积极地探索，特作总结以供商榷.

一、类比求新，探求数学知识内在的联结性

类比思维是依据两个或两类数学对象之间在某些方面的相似或相同推演出其他方面也相似或相同的一种重要思维与推理方式.通过类比思维，在类比中联想，可以达到创新知识、升华思维的目的.

图1

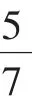
图2

图3

点评：有关类比迁移的研究表明，类比迁移是学习新技能、学习科学知识、进行科学发现和探索、培养创造性的一个重要途径.这是因为学习不仅仅是简单地增加新知识、掌握抽象规则，成功的学习经常依靠我们从记忆中提取相关的知识和技能，并以此为出发点去学习新的知识和技能，即类比迁移.因此，类比迁移的研究必将为我们学习新知识和技能、教育的改革和发展提供重要的实践意义和指导意义.

二、归纳求同，探求数学知识应用的广阔性

从不同情境问题的解法中总结共同的原理，不仅能加深对定理的理解，强化定理的应用，同时也较好地培养了学生有方向、有范围、有条理的收敛性思维方式.

案例2 在《两角和与差的正弦》教学中设计如下探究题：

题1：求sin 75°.

探究1：引导学生从题型角度思考（问题的表象）

探究2：从公式的字母意义角度思考（问题的表征）

探究3：从思维角度思考（问题的本征）

探究4：迁移到方程（问题的内涵与外延）

点评：为挖掘公式、定理的应用价值，学习中通过对上述题组的探究，从显性到隐性再到自觉性的应用，就能逐步深化，有效地加深学生对公式、定理的理解与运用.教师在教学中通过引导学生探究、发现、总结，最终探寻出问题生成、发展、延伸的“根”，让学生很好地把握了问题的本质.

三、发散求异，探求数学问题解决的多样性

发散性思维，又称求异思维，它是一种从不同的方向、途径和角度去设想，探求多种答案，最终使问题获得圆满解决的思维方法.发散性思维可以锻炼学生思维视野的广阔性，提高学生的创造力.

案例3 已知向量a=（cos θ，sin θ），向量b=（，-1），求的最大值与最小值.

方法1：通过对向量的平方求模的最值

方法2：利用模的不等量关系求模的最值

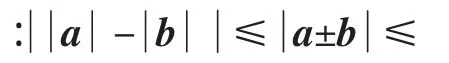
方法3：利用向量的几何含义求模的最值

图4

点评：传统教育只强调聚合思维（集中思维、求同思维、正向思维），而不强调发散思维（求异思维、逆向思维、多向思维），这是有其深刻的教育思想根源的.聚合思维要求学生对一切问题的认识理解都必须集中、统一到学科的理论体系和基本概念上来，其弊端是容易造成学生对书本、对教师、对权威的迷信，很难产生新的想法、新的思想.发散性思维，是一种从不同的方向、途径和角度去设想，探求多种渠道，最终使问题获得圆满解决的思维方法.没有发散思维就不会有任何创造性的萌芽和创造性的成果，因此发散性思维可以锻炼学生思维视野的广阔性，提高学生的创造力.

四、变式求深，探求数学方法的完备性

变式是指教师有目的、有计划地对命题进行合理的转化.如果我们能对已有的例、习题进行拓展、变式、引申，那么一方面可以培养学生积极思考的习惯，提高学生学习的兴趣；同时也达到深化理解数学知识、方法、思想的目的.

当且仅当x=时取等号.

当且仅当x=-1∈（0，1）时取等号.

当且仅当x=0时取等式号.

点评：变式教学通过变换问题的条件和结论，变换问题的形式，但不改变问题的本质，使本质的东西更凸显、更全面.变式教学注意从事物之间的联系和矛盾上来理解事物的本质，在一定程度上可以克服和减少思维僵化及思维惰性，从而可以更深刻地理解课堂教学的内容.

五、质疑求真，探求数学思维的严密性

教师以“认知冲突”为诱因创造问题情境，揭示学生认识上的矛盾，使之处于一种“心理失衡”状态，促使学生为了达到新的“知识结构平衡”，不得不去寻找探求新的理论和知识点，以弥补这种不稳定的状态.这样一方面可以纠正学生已有的认识错误，另一方面可以对学生的心理智力产生刺激，唤起学生的学习兴趣，同时也是知识建构、思维缜密递进的需要.

图5

结果显示范围扩大了，为什么？

学生讨论得出：由-3＜a＜-1-＜b＜-1，得-4-＜a+b＜-2-，扩大了a+b的取值范围.原因是什么呢？原来a，b是有联系的，即a向-3靠近时，b并不是向-1-靠近.为此，求a+b的范围还应从a，b的关系入手，那么，a，b间存在什么样的联系呢？

由a2+b2=2-2（a+b）变形为（a+1）2+（b+1）2=4，即为圆的方程，从而产生如下解法：

图6

设t=a+b，由线性规划知识可得t∈（-2-2，-4），所以ab+a+b的范围为（-1，1）.

解法2：（参数法）由（a+1）2+（b+1）2=4及（a＜b＜-1）可设

故ab+a+b=（a+1）（b+1）-1=2sin θ·2cos θ-1=2sin2θ-1，

所以得ab+a+b的范围为（-1，1）.

解法3：（不等式法）由（a+1）2+（b+1）2=4＞2（a+1）（b+1），其中（a＜b＜-1），所以0＜（a+1）（b+1）＜2，而ab+a+b=（a+1）（b+1）-1，所以ab+a+b的范围为（-1，1）.

考虑到：由图像可知，当a向-3靠近时，b正好向-1靠近；同样当a向-1-靠近时，b正好也向-1-靠近，因而可得：

解法4：由-3＜a＜-1-＜b＜-1，得-2＜a-b＜0，

从而得ab+a+b的范围为（-1，1），这样使运算过程简捷，思维明了.

点评：思维的严密性表现在能运用唯物辨证观点来观察、分析事物，能用对立统一的观点看问题，既要看到事物之间的对立，也要看到事物之间的统一和在一定条件下事物之间的相互转化，既要看到事物的正面，也要看到反面.唯物辩证法作为马克思主义哲学的宇宙观、方法论，是使人类思维具有全面性、深刻性和洞察力的根本保证，因此，在整个思维过程中只有运用唯物辨证观点作指导，才有可能使人类的基本思维形式最有效地满足思维目的的要求.

数学教学的本质是学生在教师的引导下，能动地建构数学认知结构，并得到全面的发展.数学教育的主要目标是激发学生潜能，教会学生思考，让学生变得聪明，学会数学地发现问题、思考问题、解决问题，具有创新品质，具备数学文化素养.