对数学教学中“预设”与“生成”的思考

☉

☉安徽省灵璧县教育局教研室 张桂海

☉安徽省灵璧第一中学 郑 良

凡事预则立，不预则废.因此认真钻研教材、全面了解学生、有效开发资源等精心预设是课堂良好运行的前提.教学活动的复杂性和多变性注定数学课堂教学不再是教师按预设的教学方案机械、僵化的传授知识的线性过程，无论课前的预设多么精心，当我们面对思潮千变万化的学生时，教学难免会发生诸多的意外，如果以此为起点进行冷静地思考，巧妙捕捉其中的亮点资源，并灵活地调整教学方法，机智生成新的教学方案，使教学顺利富有灵性展开，这就是教学的“生成”，它是精彩课堂的保证.

在近期各种期刊上均能看到作者相继而动，驾驭课堂的教学“预设”与“生成”，冷静思考，很多案例难言精彩，甚至是败笔，下面浅谈个人看法，与原文作者商榷，并求教于诸位专家与同仁.

一、“预设”与“生成”要确保科学

“千教万教教人求真，千学万学学做真人.”科学性是一切活动的根本，是教学的前提条件，否则教学的艺术性将成毫无意义的空谈.遗憾的是，很多情况下教师面对学生提出的“陌生”问题，想当然地给出了错误的答案.无论“预设”还是“生成”，均要三思而后行，决不能不自觉的教给学生错误的知识、思想方法，这也是教师示范作用的最基本要求.

例1 （文［1］问题2）（1）若函数f（x）=x2，定义域A={0，1，2}，求值域B.

（2）若函数f（x）=x2的值域B={0，1，4}，求定义域A.

（3）若函数的定义域A={0，1，2}，值域为B={0，1，4}，这样的函数有多少个？

对于（2）问，原文利用枚举法得到定义域A.当学生给出结果后，教师可以（预设）提问：为什么A的个数为9呢？引导学生换个角度来认识：构造集合A1={0}，A2={-1，1}，A3={-2，2}，分别从A1，A2，A3中抽出至少一个元素构成集合A即可，根据乘法原理，定义域A的个数为1×3×3=9，有利于学生对此类问题的理解，强化学生对计数原理的认知.文［1］对（3）问的解答（根据函数的定义，符合条件的函数个数是=3×2×1=6）是错误的.混淆了对应（从A到B的一一对应关系有6个）与函数（有无数个）的概念，比如构 造 函 数f（x）=ax2+bx+c（g（x）=abx+c（b＞0））等 ，利 用.确定函数需要三要素：定义域、对应法则、值域，而定义域、对应法则决定值域，如果用两个要素确定函数，只能为定义域、对应法则，这也是（1）的结果确定、（2）有9种可能、（3）有无数个函数的根本原因.

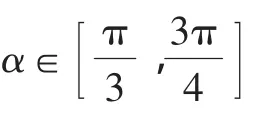
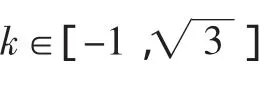
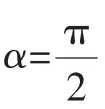
二、“预设”与“生成”要追求高效

教师对学生的引领要尽可能追求高效，最起码必须有效.很多教师面对学生的新问题，利用经验主义，即兴“生成”，点出知识、指出思路，结果学生沿途行进，无功折返.长此以往，学生就会产生对教师的不信任，逐步降低学习数学的兴趣.当然故意设置陷阱，让学生迷途知返，深思成因另当别论.文［2］在“高效的复习课——美于‘意外’的生成”中提到：…高三复习课既需要教师在课前精心预设，更需要教师充分发挥自己的教学机智，及时捕捉课堂中的生成资源，使课堂焕发出生命的活力.

文［2］指出：学生很快给出解法：

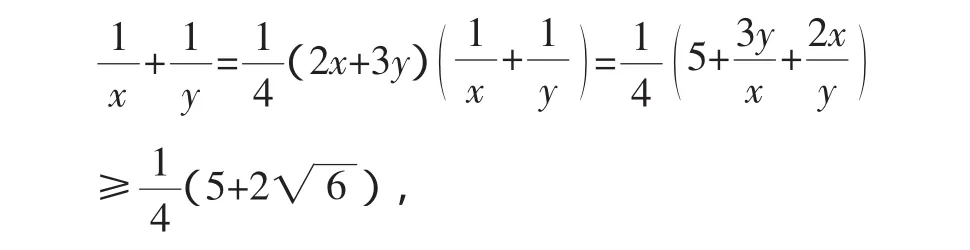
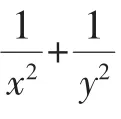
若解答这一问题，肯定要花去不少时间，影响教学进度；敷衍过去吧，显然要打击学生的积极性，降低学生的学习热情，更为严重的是，学生将会失去一次难得的探究时机和素材.最后笔者调整预设，鼓励学生进行探究，为了便于解决问题，将条件变得简单一些：把2x+3y=4改成x+y=2，两分钟后，就有几名学生获得了解决问题的途径.

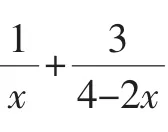
教学中应该有精彩的“预设”，更要有（有效的）动态“生成”.让学生从思维起点出发，放开手脚对问题进行探究，暴露思维过程，展现原始想法，给学生一个“本真”的解题过程，从师生思维的现场交流互动中得到解题启示.如：

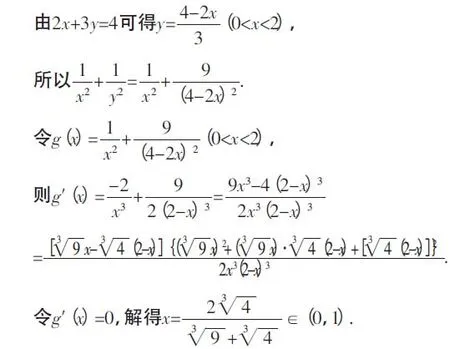
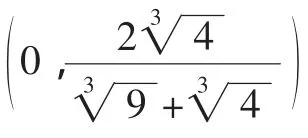
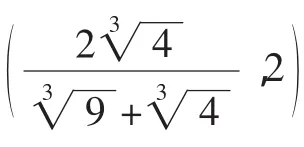
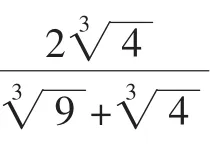
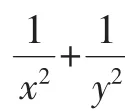
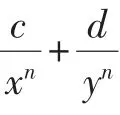
通过以上的有效“生成”，学生更加乐于思考，善于思考，积极培养创新意识，加之教师的较满意解答，加强对教师的信任，勇于向教师挑战，刨根问底，探寻问题的本质.

三、“预设”与“生成”要贴近自然

著名数学家希尔伯特师从拉撒路·富克斯学习微分方程，从导师对要讲内容在课堂上现想现推的教学中“得到一个机会，瞧一瞧最高超的数学思维的实际过程”，领悟到一个数学家是如何自然、真实、合理思考问题的过程，这种启发超越任何一本教材.人教A版高中数学教材“主编寄语”指出：数学是自然的，数学是清楚的.同样，数学教学的“预设”和“生成”也应与学生自然合理的想法相依，而不能是教师的强行“灌输”.课前的“预设”和课内的“生成”要根据当时的具体情况，巧妙地在学生不知不觉中做出相应的变动.切实对接学生认知、融合课堂变化，自然合理的以学定教，思路自然学生才能学得会.

例4 （文［2］案例2）已知cos α+2sin α=-，求tan α.

本题为2008年高考数学浙江卷理科第8题（原题为选择题），文［2］给出两种解法，均为通性通法，本题还有其他解法，如两边平方齐次化等，不再详述.文［2］给出探究过程：还有更简捷的解法吗？学生积极思索，没有头绪.教师提示：对一个不等式的两边同时求导，可以吗？试试看.…教师：这位同学真厉害，这种巧合是我特意设计的.因此，对于本题，两边求导得到的结果正确，但条件变为cos α+2sin α=m（m∈R），就不一定可行了.

教师精心“预设”，试图通过此例复习导数的知识，体会在等号两边同时求导的解题方法，引领学生走出导数认知上的误区.精心“预设”仅仅是教师对课堂上可能发生情况的一种应对方案，不一定要按部就班执行，否则就会无视学生的课堂主体地位，变成了灌输，强行把学生“诱导”到教师设定的轨道上来.从文中可以看出，学生根本就没有从导数入手的想法，在教师的指令下，尝试求导，发现巧合，寻找根源.笔者认为完全没有必要，导数在中学数学中的作用毋庸置疑，鉴于课标要求，学生认知水平，在三角函数、数列中大量介入导数可能导致学生更多错误的发生.“清水出芙蓉，天然去雕饰”，学生的自然想法是最重要的，教师的灌输导致学生学习的囫囵吞枣，消化不良.学生的错误应该由学生自觉发现，经过深思熟虑解决，这个过程教师引而弗牵，当好“助产婆”的角色.案例中有可能把学生引入歧途.也许学生会认为三角函数应该多用导数来强化，因为学生没有解三角方程（不等式）的能力，同时舍弃完整的三角函数体系另寻他法，无异于放弃修好的高速公路不走重建羊肠小道；若学生放弃导数在三角函数中的应用，无疑割裂了知识之间的联系.一般说来，概念教学中强调正例、反例的应用，能加深学生对问题本质的认识.习题教学中，让学生的错误在自然中流淌，只有学生经历过的，印象才是最深刻的，教师完全没有必要预设各种错误，牵着学生下水再去救人，可能出现“教师不提，学生不错，教师强调，学生犯错”的尴尬局面.

四、“预设”与“生成”要保证适切

学之道在于悟，教之道在于度.“预设”和“生成”不能靠教师的一厢情愿，必须以学生为基础，因材施教，否则可能导致学生吃不饱或消化不了.

“预设”和“生成”好比课堂教学的两个翅膀，是课堂教学整体的两个方面，只有它们满足科学、高效、自然、适切等，课堂才能飞得更高、飞得更远.在教学中，应尽可能多的“把时间还给学生，把机会留给学生”，切实理解数学、理解教学、理解学生，在学生知识、思维基础上，小步前行，将“预设”与“生成”完美演绎，着力提高学生的数学素养.

1.孙居国.高三数学教学中选题的思考［J］.中学数学教学参考（上旬刊），2012（10）：39-41.

2.陈余根.高考数学复习课的现状分析及对策研究［J］.中学数学教学参考（上旬刊），2012（10）：42-44.

3.章建跃.注重通性通法才是好数学教学［J］.中小学数学（高中版），2011（11）：封四.

4.刘瑞美.合理预设与精彩生成是一个动态的过程［J］.中学数学研究（上半月），2012（5）：4-7.