“数学化”思想在导数概念教学中的应用

☉贵州师范大学数学学院 吴沛东

☉贵州省贵阳市第二中学 卢焱尧

☉贵州师范大学数学学院 夏小刚

数学化思想突出地表现为具有强烈的“用数学”的意识.人们运用数学的方法观察现实世界、分析研究各种具体现象，并加以甄别、整理、归类，以发现其规律，这个过程就是数学化.数学的产生与发展本身就是一个数学化的过程，人们从结绳记事或石块堆集形成数的概念；从测量、绘画形成图形的概念，是数学化；数学家从具体的置换群与几何变化群抽象出群的一般概念，这也是数学化.数学的整个体系，作为充满着各种各样内在联系与外部关系的整体结构，它并非是一个僵化的、静止的框架，它是在与现实世界的各个领域的密切联系过程中发生、形成并发展起来的.就像线性函数起始于自然和社会中的比例关系，数量积开始于力学，以及导数开始于速度、加速度等.所以说，整个数学体系的形成就是数学化的结果.

一、数学化的涵义

1.“数学化”的基本对象

弗赖登塔尔认为：数学化就是数学地组织现实世界的过程.同时他所强调的数学化的对象可分为两类，一类是现实客观问题——事物，另一类是较为具体的数学问题即数学本身.

需要强调的是，数学化是一个过程，是从问题开始，由实际问题到数学问题，由具体问题到抽象概念，由解决问题到推广应用的一个教育全过程，而不是方程、函数、向量等具体的数学素材.把数学化作为数学课本教学的组成部分，是要使课本成为学生自己去“发现”一些已有数学结果的辅导书［1］.

2.“数学化”的两种方式

弗赖登塔尔引用了埃德里安·特雷弗斯（Adrian Treffers）关于数学化的理论.特雷弗斯用垂直和水平两个方向表示数学化，垂直方向由低到高是指数学的发展程度，即对数学本身进行数学化（从符号到概念的数学化），通俗地讲，在数学范畴之内对已经符号化了的问题作进一步抽象化处理.既可以是某些数学知识的深化，亦可以是对已有的数学知识进行分类、整理、综合、构造，以形成不同层次的公理体系和形式体系，使数学知识体系更系统、更完美.

垂直数学化过程可表示如下：猜想公式→证明一些规则→完善模型→调整综合模型→形成新的数学概念→一般化过程（现实的、构造的）.

水平方向是指不同的现实（包括数学本身）内容即对客观世界进行数学化（从实际问题转化为数学问题的数学化），通俗地讲，发现实际问题中的数学成分，并对这些成分做符号化处理.结果是数学概念、运算法则、规律、定理和为解决具体问题而构造的数学模型等.数学化可以包括公理化、形式化以及模式化.

水平数学化过程可表示如下：从背景中识别数学→图示化→形式化→寻找关系与规律→识别本质→对应到已知的数学模型（现实的，经验的）.

弗氏认为：任何数学都是数学化的结果，不存在没有数学化的数学，不存在没有公理化的公理，也不存在没有形式化的形式［2］.弗赖登塔尔指出数学学习过程是垂直和水平两个方向的数学化的过程.

特雷弗斯从数学化的角度出发，对教学过程的模式区分为如下四种（如表1）：

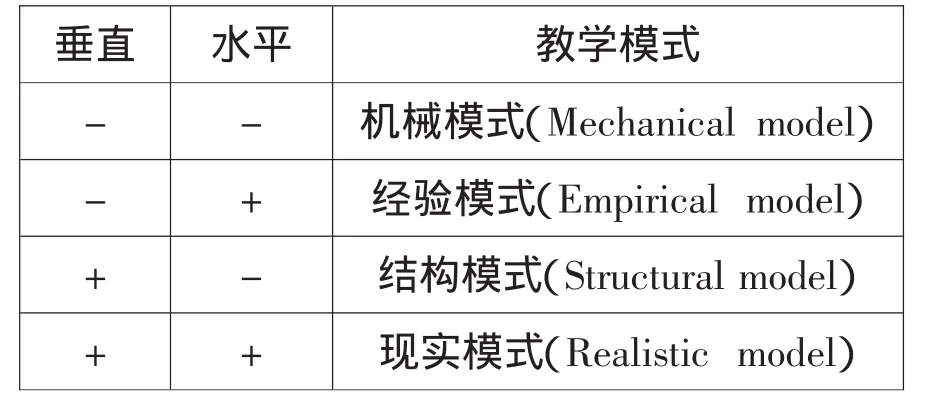
表1 “数学化”的教学模式

表中“+”表示“有”，“-”表示“没有”，所示的四种模式是根据垂直和水平两个方向所强调的程度不同来区分的［3］.

弗赖登塔尔教授和他的同事们的研究表明，按现实模式学习数学，学生能达到较高的数学化水平.

3.“数学化”教学思想的实质

“数学现实”与“数学化”这两点合起来构成了现实数学教育思想的精髓，它可以对数学化教学的含义做出科学的阐释，所以说“数学化”是数学现实教育的主题.大量心理学研究表明，人们在理解数学知识时，如果有了具体事物的支持，从实际情境入手，再逐渐过渡到逻辑思维，这样比直接接受理论知识要理解得更深刻，记忆得更牢固.

那么，“数学化”的真正含义是什么？目前，大多数人对“数学化”的理解是：数学地观察、思考实际问题，并且应用数学知识来解决实际问题.事实上，前面的理解不够全面，“数学化”还应包括：对现实世界的客观事物的数学化，实现数学知识的“再创造”.由此可知：“数学化”不仅是数学知识的应用，也可以是数学知识的“再创造”.图1可视为“数学化”的全面理解.

图1“数学化”教学思想的实质

所以，我们可以把数学化的含义概括为：人们运用数学的语言、知识、方法、思想、观点等来观察、分析、研究客观世界中的各种问题和现象，并加以整理组织，得到相关知识和规律的过程.

二、新课标下基于“数学化”思想的导数概念教材分析

1.导数概念教学内容的变化

自2003年《普通高中数学课程标准》实验稿（以下简称《标准》）颁布后，不同版本的高中数学教材相继出版.2004年秋，山东、广东、海南、宁夏等四个省区作为第一批实验省区开始使用新教材.

《标准》对“导数及其应用”内容的要求相比以往教材有很大的变化，要求把导数作为一种重要的数学思想、方法来学习，提高对导数应用性的要求，降低了对求导计算和定积分计算的要求.《标准》的定位是：用导数反映的变化率思想研究初等函数的性质.首先，中学微积分不宜求全，不必从一般极限概念讲起，而是直接引入导数，即变化率的思想（它是人类思维进步的里程碑）.当需要涉及极限时，只要直观认识即可.这样，把完整的微积分理论放到大学，中学阶段学习导数，既为大学做铺垫，也为日后不学微积分的学生提供理解变化率思想的机会.其次，中学讲导数有助于进一步理解函数的变化性态.例如，可以从观察y=x2的切线的斜率开始，判断它的单调下降、上升区间和极值；高中阶段用导数求单调区间、求极值、证明不等式，可以体现它在中学数学里的价值.

来自实验地区的相关信息表明：“导数及其应用”作为《普通高中课程标准实验教科书·数学》（以人教版教材为例，以下简称《新教材》）的一个重要模块（选修2-2），它加大了由传统教材的“常量数学”向“变量数学”倾斜的力度，体现了新一轮基础教育改革课程内容选编所应遵循的原则：“时代性、基础性、大众性、选择性”［4］.其地位和作用已引起国内数学教育界的广泛关注.导数融数形于一体，既介绍求导的运算，导数的几何意义，又阐述根据导数判断函数在给定区间内的单调性，以及导数在日常生活中关于极、最值问题的应用.其应用价值不言而喻，这部分内容的选取和编排就现阶段来看是合适的，更是必要的.

2.导数概念教学的基本要求

在导数概念的引入方面，《标准》要求：通过对大量实例的分析，经历由平均变化率过渡到瞬时变化率的过程，了解导数概念的实际背景，知道瞬时变化率就是导数，体会导数的思想及其内涵；通过函数图像直观地理解导数的几何意义［5］.教学内容与要求可用图2来表示.

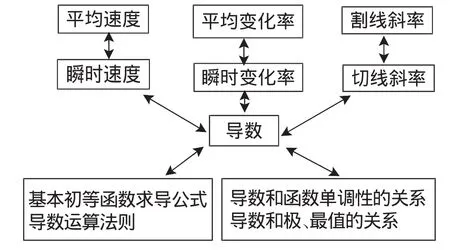
图2

可见《新教材》对该模块的处理重在突出导数概念的本质，而“不是在学习一般极限的基础上，把导数作一种特殊的极限（增量比的极限）来处理，而是直接通过实际背景和具体应用实例——速度、膨胀率、效率、增长率等反映导数思想和本质的实例，引导学生经历由平均变化率到瞬时变化率的过程，认识和理解导数概念，在对实际背景问题研究的基础上，抽象概括出导数的概念”［6］.这种直观引入的方法，由简单到复杂，由直观到抽象，既体现“数学化”的实用性和产生源头，更有利于高中生的接受与理解.因此，高中阶段的教学任务应是侧重培养学生对“变化率”的认识，通过函数的图像加深学生对导数概念的理解.

三、基于“数学化”思想的导数概念教学设计

1.导数概念的引入

在现实生活中，大家经常看到储油罐、拱形涵洞等设计与建筑，除了美观和利用力学原理外，其科学性和实用性与我们要学习的导数息息相关！接下来请看两个身边的例子.

示例1：商店里的罐装汽水、可乐、啤酒等，大多是圆柱铝罐，这是为什么呢？

示例2：如果容积不变，什么形状的包装用料最省？

实际上，这样的问题都可以归结为求函数的最值问题.一般函数求最值很简单，但对于一些复杂函数我们用什么办法呢？今天学习的导数就可以解决这样的问题！导数是解决函数极、最值问题的有力工具，它不仅可以解决极、最值问题，还能解决一些复杂曲线的切线问题.

【设计意图】让学生明白身边实例，是学习新课的最好素材，为下面知识讲解打下伏笔.

（1）横向数学化——由现实世界转向数学知识

师：大家回忆一下，平均速度的文字叙述和计算公式是什么？

生1：平均速度是指在某段时间内物体运动的位移与所用时间的比值.它是矢量，有方向性；表示物体在时间间隔△t内的平均快慢程度.

生2：△s=s（1）-s（2）；△t=t（1）-t（2）；平均速度=△s÷△t.

我们知道，当运动员从10米高台跳水时，从腾空到进入水面的过程中，不同时刻的速度是不同的.假设t秒后运动员相对地面的高度为：H（t）=-4.9t2+6.5t+10，在2秒时运动员的速度为多少？［7］

解：该运动员在2秒到2.1秒（记为［2，2.1］）的平均速度为

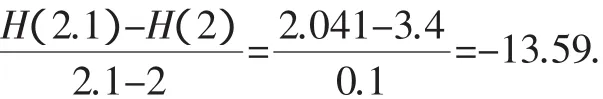
同样，可以计算出［2，2.01］，［2，2.001］，…的平均速度，也可以计算出［1.99，2］，［1.999，2］，…的平均速度（如表2）.

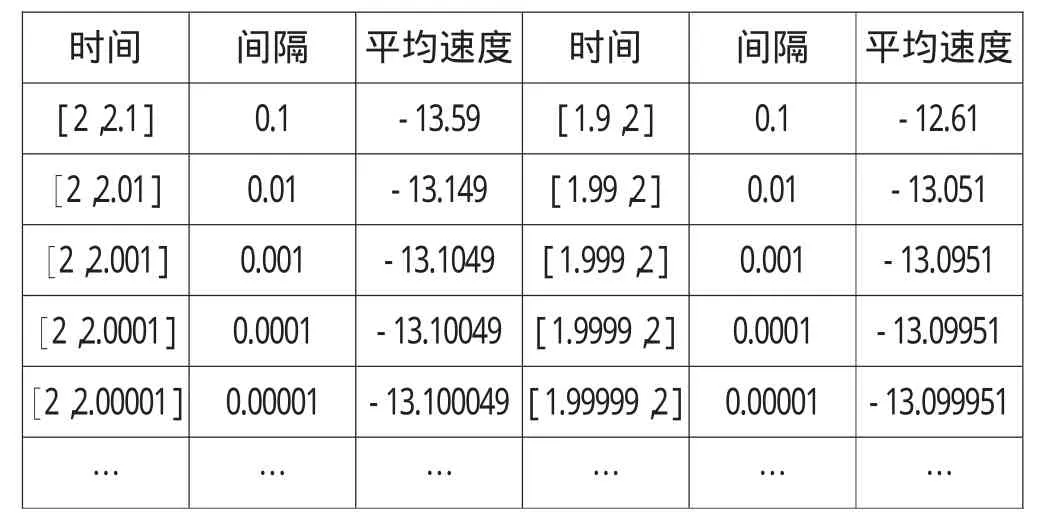
表2 无限小时隔平均速度的计算

师：大家可以看到，当时间间隔越来越小时，平均速度趋于一个常数，这一常数（13.1）就可作为该运动员在2秒时的速度！同学们考虑：为什么可以这样表示？这样表示的理论依据是什么呢？

【设计意图】循序渐进，激发学生的兴趣和深思，挖掘深层次内涵.

（2）回顾旧知，引导学生研究实际问题

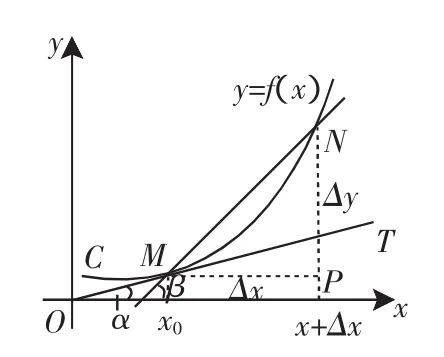
图3 割、切线的渐近过程

师：（几何画板演示，如图3所示）已知曲线C是函数y=f（x）的图像，M是曲线上一点，坐标为（x0，y0）.在点M附近取一点N，坐标为（x+△x，y+△y），分别过M、N作MP∥x轴，作NP∥y轴.设割线MN的倾斜角为β，切线MT的倾斜角为α，那么MN、MT倾斜角的正切值之间有什么关系？用△x、△y表示.

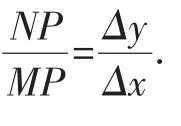
师：那么割线MN的斜率为多少？

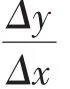
师：现在M点不动，N点沿着曲线顺时针运动，并且无限地向点M逼近，大家观察N点的运动情况.（几何画板演示）这个过程表示为△x→0.这时这条割线MN与点M的切线是什么关系？

生众：与在点M处的切线重合.

师：我们是通过运动的方式得到切线的，那能不能根据这种过程来定义切线呢？请同学们利用几何画板，画出你喜欢的一条曲线，按照老师的做法，看是否可以得出同样的结果？

师：（学生利用几何画板进行尝试）怎么样？大家的结论是什么？

生4：我们可以这样定义切线：当点N沿着曲线顺时针无限接近M点时，割线MN的极限位置叫做曲线在点M处的切线.所以可以用割线MN的斜率的极限，定义曲线在点M处的切线的斜率.

师：我们通过观察点N的运动得到了切线.因为运动的过程就是取极限的过程，所以可以用极限来定义切线和切线的斜率.

这个环节通过几何画板演示，学生经历探索曲线的切线方程的过程，体会到抽象的数学问题转化为形象化数学问题的方法.从而，培养用运动的眼光去理解数学问题的能力，感受从实际问题的探索中，尝试几何画板的操作技能，发现极限和导数等概念的应用价值.增强了学生对数学活动的兴趣和自信心！

【设计意图】由生活到实际问题步步逼进，培育学生主动思考，强化知识迁移.

2.导数概念的理解

（1）纵向数学化——应用学科知识，链接迁移，培养学生发散思维

师：同学们，速度是我们较常见且熟悉的概念，大家是否知道瞬时速度和平均速度之间也具有类似的极限关系呢？请大家讨论一下！

生5：（讨论后）要确定物体在某一点M处的瞬时速度，从M点起取一小段位移S，求出物体在这段位移上的平均速度.正如前面跳水的例子，当这段位移ΔS→0时，平均速度可以近似地表示物体经过M点的瞬时速度.

师：大家知道，物体的运动规律用函数表示为S=S（t），称为物体的运动方程或位移公式.现在有两个时刻t0，t0+Δt，问：从t0到t0+Δt这段时间内，物体的位移和平均速度各是多少？

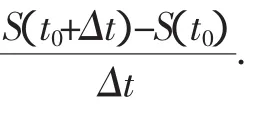
师：根据对瞬时速度的直观描述，当位移足够小，位移由时间t来表示，也就是说时间足够短时，平均速度就等于瞬时速度.如何来刻画时间足够短呢？现在是从t0到t0+Δt这段时间记为Δt.

生众：时间Δt足够短，就是Δt无限趋近于0.

师：当Δt→0时，平均速度就越接近于瞬时速度，那么用极限如何表示瞬时速度呢？

【设计意图】由导数概念的物理意义入手，巩固旧知，揭示导数概念的本质，为导数概念的引出做最终铺垫.

（2）讨论分析，得出导数的定义

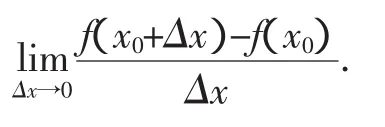
师：这个概念：

①提供了求曲线上某点处的切线的斜率的一种方法；

②切线斜率的本质——函数平均变化率的极限.

下面我们归纳导数的定义：

（3）纵向数学化——导数内部知识调整，总结其几何意义

图4 导数的几何意义

f′（x）表示曲线y=f（x）在点M（x0，f（x0））处的切线的斜率，即f′（x0）=tan α（α为切线倾斜角）（如图4）.

当f′（x0）=0时，切线与x轴平行，x0称为驻点；切线方程为：y=f（x0），法线方程为：x=x0.

当f′（x0）→∞时，切线与x轴垂直，切线方程为：x=x0；

法线方程为：y=（fx0）.

当f′（x0）≠0且存在时，点M（x0，y0）处的切线方程为：

【设计意图】导数概念的纵向数学化提升，揭示它在本学科内的本质及价值.

（4）导数知识迁移升华，体现其应用价值

利用导数的符号判断函数的增减性，这是导数几何意义在研究曲线变化规律时的一个应用，它充分体现了数形结合的思想（如图5）.y-y0=f′（x0）（x-x0）；

图5

从图5我们可以得出如下结论：当f′（x0）＞0时，曲线过点M上升；当f′（x0）＜0时，曲线过点M′下降；

一般地，在某个区间（a，b）内，如果f′（x）＞0，那么函数y=f（x）在这个区间内单调递增；如果f′（x）＜0，那么函数y=f（x）在这个区间内单调递减；如果在某个区间内恒有f′（x）=0，则f（x）是常数函数.

注意：在某个区间内，f′（x）＞0是f（x）在此区间上为增函数的充分条件，而不是必要条件，如f（x）=x3在R内是增函数，但x=0时f′（x）=0.也就是说，如果已知f（x）为增函数，解题时就必须写f′（x）≥0.

【设计意图】导数概念进一步升华，回归生活体现其价值精髓——横、纵数学化的辩证统一，源于生活，服务于生活！

“数学化”思想是数学认识从感性上升为理性的必由之路.该思想的培养不是一朝一夕的事情，这项任务应该贯穿于整个数学教育的过程中.重要的是要在教学过程中有意识地体现数学化的思想，培养学生数学化的意识，并采取有效的措施渗透和强化这一思想.通过数学化与导数概念教学的认识，提出与导数概念教学相关的两点建议：

其一，把握导数的本质，处理好展现数学与发现数学的逻辑关系：

导数的概念教学完全可以还原牛顿的最初目的——确定变速运动的速度，完全可以还原莱布尼兹的最初目的——定义切线的概念，但二者并没有给出完全的形式化定义，更没有建立完整的极限理论，所以我们完全可以不受大学数学教材体系的局限，不用逻辑发展的手段提出定义，而是还原导数“创造”的本质，还原导数“再创造”的思维过程，教给学生高等数学的思维过程.

其二，把弗赖登塔尔的“数学化”思想融入教学，处理好现实化与数学化的关系：

数学教育的正确途径应是现实的数学化途径，是数学抽象发展与现实世界的紧密结合.导数教学所需要的课程体系应该全面而完善地体现数学化的正确发展，既要强调现实基础，又要重视逻辑思维，帮助学生实现向高等数学思维的转变.以学生的实际思维方式为基础，将形式数学本身置于人类活动的观点中，设法把复杂的人类思维组织成一个逻辑体系.从而，为学生提供高层次数学思维训练平台，提高数学素养.

1.张奠宙，宋乃庆.数学教育概论［M］.北京：高等教育出版社，2 0 0 4.

2.H·弗赖登塔尔.唐瑞芳译编.弗赖登塔尔教授关于数学教育的问答［J］.数学教育，1 9 8 8（2、3、4）.

3.《2 1世纪中国数学教育展望》课题组.2 1世纪中国数学教育展望(第一辑)［M］.北京：北京师范大学出版社，1 9 9 3.

4.缪雪松.微积分思想发展史的教学启示［J］.数学教育研究，2 0 0 4（1）：3 6-3 7.

5.华东师范大学数学系.数学分析（上）［M］.北京:高等教育出版社,2 0 0 1：8 7-1 6 0.

6.教育部基础教育司、师范教育司组织编写《数学课程标准研修》［M］.北京：高等教育出版社,2 0 0 4：9 9-1 0 0.

7.教育部制订《普通高中数学新课程标准（实验）》［M］.北京：人民教育出版社,2 0 0 3：4 4-4 5.