构造法在高等代数中的应用研究

史秀英

（赤峰学院继续教育与教师培训学院，内蒙古赤峰024000）

构造法在高等代数中的应用研究

史秀英

（赤峰学院继续教育与教师培训学院，内蒙古赤峰024000）

构造法是一种富有创造性的解题方法，利用构造法解题有出奇制胜之妙，也有事半功倍之效.本文将以高等代数有关知识并结合具体实例，谈谈构造思想方法在解题中的运用.

构造法；高等代数；应用；数学模型

构造法属于非常规思维、另辟蹊径的解题方法，其本质特征是“构造”，用构造法解题，无一定之规，表现出思维的试探性、不规则性和创造性，其关键在于对问题特征的敏锐观察，展开丰富的联想，充分地挖掘题设与结论的内在联系，恰当地构造数学模型，进而谋求解决问题的途径.

构造法在高等代数中有着广泛的应用，但怎样“构造”始终是求解问题的难点.在具体研究对象中，根据实际情况可能需要构造函数、构造多项式、构造行列式、构造矩阵、构造二次型、构造基、构造变换等等数学模型，而后再利用已知条件及有关概念、定理推理得出所要证明的结果.构造法的解题类型较多，一般存在性命题或潜在的存在性命题更适宜用构造法.

1 构造法在多项式理论中的应用

构造法在多项式理论中的应用，主要是借助已知条件，利用多项式的性质，构造出符合条件的多项式，进而最终获解.

例1证明任意一个次数大于零的有理系数多项式都可以表成两个有理数域上的不可约多项式的和.

分析：本题中讨论的是任意多项式的一种定性分解，因此，本题的解决必须要定性地构造出结论中的表示形式.问题的关键是这两个有理系数不可约多项式如何构造，而我们常见的不可约有理系数多项式有一次多项式和满足Eisenstein判别法条件的有理系数多项式.

（ⅰ）若a0=0，取素数p，构造多项式：g(x)=pf(x)+x'+p，其中s>n，由Eisenstein判别法可得：g(x),h(x)=x'+p在有理数域上不可约，所以在有理数域上也不可约.

（ⅱ）若a0≠0，取素数p，使得：p†a0，p>2，构造多项式：g (x)=pf(x)+x'+p(p-2)a0，其中s>n，g(x)的常数项为：pa0+p(p-2) a0=p(p-1)a0，可见：p2†p(p-1)a0，由Eisenstein判别法知：g(x),h (x)=x'+p(p-2)a0在有理数域上不可约，所以h (x)在有理数域上也不可约.

（2）若f(x)∈Q[x],则存在m∈z，使mf(x)∈Z[x]，由（1）知：存在有理数域上不可约多项式u(x),v(x)∈Q(x)，使得mf(x)=u (x)+v(x)，故

2 构造法在行列式中的应用

构造法在行列式中的应用，主要是借助已知的特征、特型和特值行列式，利用行列式的性质与展开，构造恒等变形行列式，进而最终获解.

例2证明：n阶循环行列式中1,ε,ε2,…,εn-1为全部n次单位根（其中ε为n次本原单位根），f(x)=a1+a2x+…+anxn-1.

分析：根据本题行列式的特征，构造矩阵，利用特征多项式、特征值来证.

证明构造n阶方阵：

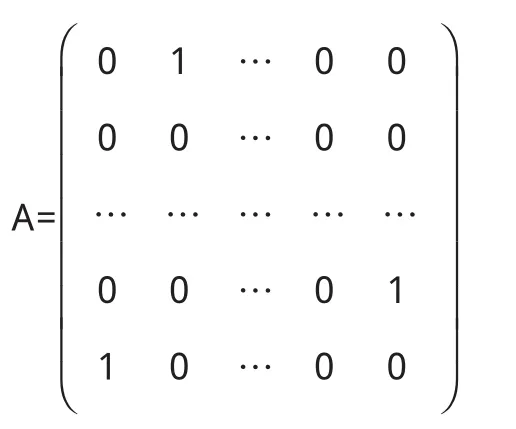
则Dn=a1E+a2A+…+anAn-1=f（A），且A的特征多项式为|λE-A|=λn-1，即有A的特征值为全部n次单位根ε1,ε2,…,εn,有矩阵f(A)的特征值为f(ε1),f(ε2),…,f(εn)，所以|Dn|=|f(A)|=f(ε1)f (ε2)…f(εn).

3 构造法在线性方程组中的应用

构造法在线性方程组中的应用，主要是借助已知条件，利用线性方程组的同解变换，构造同解方程组，进而最终获解.

例3设n阶方阵A的秩为r，则存在秩为n-r的n阶矩阵B和C,使得AB=0,CA=0.

证明设齐次线性方程组AX=0的基础解系为ξ1,ξ2,…, ξn-r，构造矩阵：B=（ξ1,ξ2,…,ξn-r,ξn-r+1,…,ξn），其中ξn-r+1,…,ξn是ξ1,ξ2,…,ξn-r的线性组合，则有Aξi=0（i=1,2,…,n），即AB=0.

同理，构造矩阵F,使得A'F=0,于是F'A=0,令F'=C，即有CA=0.

4 构造法在矩阵中的应用

构造法在矩阵中的应用，主要是借助已知条件，利用矩阵的性质，构造出符合条件的矩阵或矩阵等式，进而最终获解.

例4设矩阵A∈Ps×n，证明：r(Es-AA')-r(En-A'A)=s-n

于是有r(B)=r(Es-AA')+n=s+r(En-A'A).故：r(Es-AA')-r(En-A'A)=s-n.

5 构造法在二次型中的应用

构造法在二次型中的应用，主要是借助已知条件，利用二次型与对称矩阵的性质，构造出符合条件的二次型或对称矩阵，进而最终获解.

例5设A实数域上的n阶对称矩阵，求证：存在实数c，使得对实数域上任何n维列向量X,都有|X'AX|≤cXX',其中X'是X的转置矩阵.

证明由于A是对称矩阵，构造n元二次型

f(x1,x2,…,xn)=X'AX,则存在正交线性变换X=QY，将二次型化成标准型

另取c=max{|λ1|,λ2|,…,|λn|}，

则有-cX'AX=-cY'Q'QY=-cY'Y

于是|X'AX|≤cX'X.

6 构造法在线性空间中的应用

构造法在线性空间中的应用，主要是借助已知条件，利用线性空间基的性质，构造出符合条件的向量，进而最终获解.

例6设V数域R上一个n(n≥1)维线性空间，证明：存在V的无限子集S，使S中任意n个向量线性无关.

证明设β1,β2,…,βn为V的一组基，则V=L(β1,β2,…, βn)，从而对任意的α∈V，有其中k1,k2,…,kn∈R，特别的，我们构造如下向量

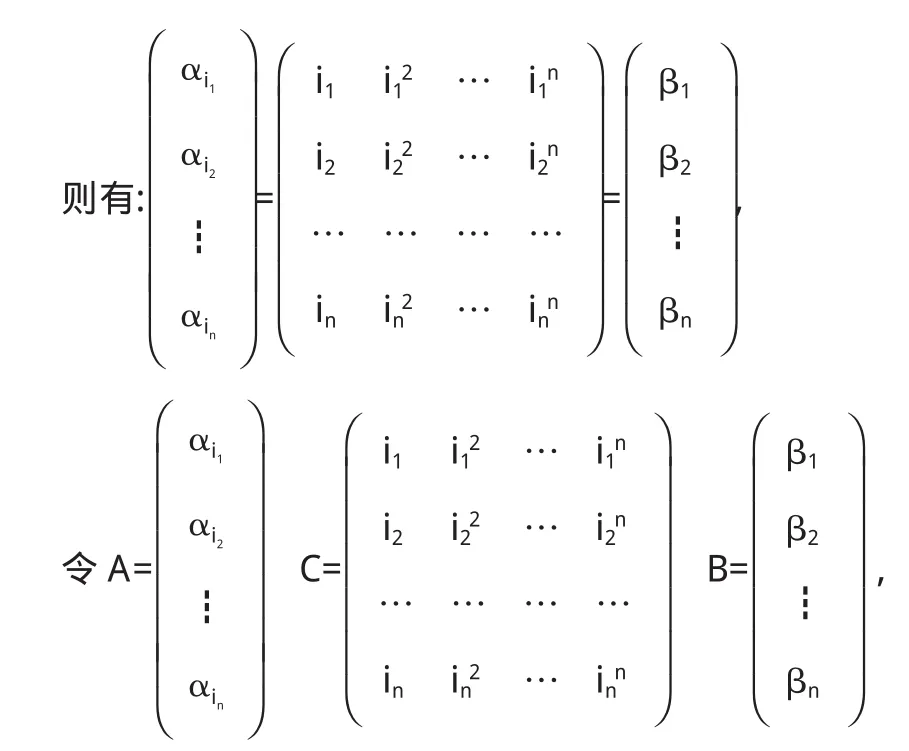
即A=CB.

由于ik≠ij≠0，从而由范德蒙行列式可知：≠0，即有r(C)=n，而β1,β2,…,βn为V的一组基，所以r(B)=n，于是r(A)=n.

7 构造法在线性变换中的应用

构造法在线性变换中的应用，主要是借助已知条件，利用线性变换与矩阵的同构与性质，构造出符合条件的线性变换与矩阵，进而最终获解.

例7设V是一个n维线性空间，证明：V的任意一个子空间W必为某线性变换的核.

证明当W={0}时，则W为恒等变换的核；

当W=V时，则W为零变换的核；

当{0}⊂W⊂V时，即W是V的真子空间时，设dimW=r，

取W的一组基：ξ1,ξ2,…,ξr，把它扩充为V的一组基：ξ1, ξ2,…,ξr，ξr+1,…,ξn，

8 构造法在欧式空间中的应用

构造法在欧式空间中的应用，主要是根据题设条件和结论的特征，利用欧式空间的性质，构造出符合条件的结论，进而最终获解.

例8设V是一个n维欧式空间，W是V的子空间，W⊥是V中一切与W正交的向量组成的集合，证明：W⊥是V的子空间，且dimW+dimW⊥=n，(W⊥)⊥=W

证明易证W⊥是V的子空间.

当W={0}时，易知W⊥=V，这时V=W⊕W⊥.

当W=V时，易知W⊥={0}，这时V=W⊕W⊥仍成立.

当dimW=t(0

构造子空间：W1=L(εt+1,…,εn),可以证明W1=L(εt+1,…,εn) =W⊥.

事实上，任取α∈W1=L(εt+1,…,εn),则α=at+1εt+1+…anεn，任取β∈W,则

于是α∈W⊥，即W1=L(εt+1,…,εn)⊆W⊥.

反之，任取γ∈W⊥⊆V,不妨设γ=b1ε1+b2ε2+…+btεt+bt+1εt+1+…+bnεn,对任意εi∈W(i=1,2,…,t)，则有(εi,γ)=bi(εi,εi) =0,即有bi=0(i=1,2,…,t)，

故γ=bt+1εt+1+…+bnεn，从而γ∈L(εt+1,…,εn)=W1,即W⊥⊆L (εt+1,…,εn)=W1，

从而W1=L(εt+1,…,εn)=W⊥.

又V=L(ε1+ε2+…+εt,εt+1+…+εn)=L(ε1,ε2,…,εt)⊕L(εt+1,…, εn)，即V=W⊕W⊥.由V=W⊕W⊥，且W⊥W⊥,所以由欧式空间正交补的定义及唯一性可知：(W⊥)⊥=W.

以上，我们从高等代数不同的知识角度谈了构造法的应用，更多用构造法求解的问题，还需要我们在以后学习过程中去总结发现.

〔1〕王积社，杨晓鹏.高等代数典型问题精讲[M].北京：科学出版社,2010.

〔2〕周金土.高等代数解题思想与方法[M].杭州：浙江大学出版社,2008.

〔3〕李志慧,李永明.高等代数中的典型问题与方法[M].北京：科学出版社,2008.

〔4〕张禾瑞,郝鈵新.高等代数[M].北京：高等教育出版社, 1999.

O151.2

A

1673-260X（2013）06-0011-03