Hamilton体系的辛算法

王颜超，邓亚莉

（内蒙古大学，内蒙古呼和浩特010021）

Hamilton体系的辛算法

王颜超，邓亚莉

（内蒙古大学，内蒙古呼和浩特010021）

本文介绍了辛空间的基本理论,通过构造辛算法得到Hamilton方程的数值解，并与分离变量法得到的解进行了比较.

Hamilton体系；辛算法；辛空间

在自然界中很多数学物理问题均可以用Lagrange方程或Hamilton方程表示,而Lagrange方程可以通过Legendre变换为Hamilton方程.经典力学具有三种表示形式,设有n个自由度的运动,位置向量记为q=(q1,q2，…,qn)T,势能函数为V=V(q),则是运动方程的标准形式,它是在n维位形空间Rn中的2阶微分方程组,通常称为经典力学的标准形式即牛顿形式.Lagrange通过引进动能,势能差数的作用量并利用变分原理将运动方程写为它被称为经典力学的变分形式即Lagrange形式.后来Hamilton利用动量p=Mq˙和总能量H=T+V将运动方程写为称为Hamilton正则方程，它是2n维相空间中相变量(p1,…,pn；q1,…,qn)的1阶微分方程组.

作为动力系统的重要体系,Hamilton体系可以用来表示一切真实的,耗散可忽略不计的物理过程,而Hamilton体系的基础是辛几何.Hamilton将系统能量以广义坐标及广义动量来表示,构成一个2n维相空间,故经典力学可以被看成相空间中的一种几何学即辛几何学.经典力学基本定理用辛几何的语言就表示为“一切哈氏体系的动力演化都使辛度量保持不变,即就是辛(正则)变换”.因此解哈氏方程的“正确”的离散算法就应是辛变换,这种算法称为辛(正则)算法或哈密尔顿算法.

1 辛空间基本理论

通常我们比较熟悉的是以实数为坐标的欧式空间Rn,现将Rn推广到以复数为坐标的酉空间,Cn为n维复向量空间,C表示全体复数,Z=(z1,z2,…,zn),zk∈C,k=1,2,…,n.在Cn中引进Hermite内积

具有Hermite内积的复线行空间称为酉空间.在式(1.1)中,因zk∈C,故可以写为zk=xk+iξk,xk,ξk∈R,因而Cn中的向量与Rn中的向量建立一一对应关系如下:

Cn↔R2n

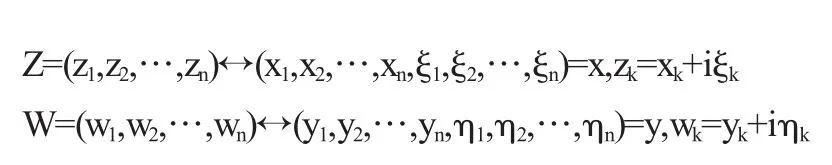
且对向量加法及用实数相乘仍保持,即:

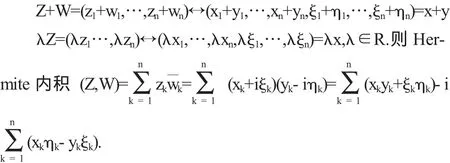
可以看出Hermite内积(Z,W)由两部分组成,实部是R2n中欧式内积,虚部可以看成是R2n中两个向量x=(x1,x2,…,xn, ξ1,ξ2,…,ξn)与y=(y1,y2,…,yn,η1,η2,…,ηn)的一种新的“内积”,我们称这种内积为辛内积[1].

定义1设W是实数域R上的一个2n维相空间,对W中的任意两个向量α,β依一定法则对应着一个实数,这个数称为辛内积,记作〈α,β〉,且辛内积〈α,β〉运算满足下列4个条件:

（1）〈α,β〉=-〈β，α〉（1.2）

（2）〈kα,β〉=k〈α,β〉,∀k∈R（1.3）

（3）〈α+γ,β〉=〈α,β〉+〈γ,β〉,γ为W中任意向量（1.4）

（4）若向量α对W中任意向量β均有〈α,β〉=0,则α=0（1.5）

称定义有这种辛内积的相空间为辛空间,辛空间与研究长度等度量性质的欧几里得空间不同,它研究的是面积,或说是研究做功的,利用它可以描述许多重要的物理现象,故近年来受到很到理论与实际工作者的重视.

R2n中两个向量x=(x1,x2,…,xn,ξ1,ξ2,…,ξn)与y=(y1,y2,…,yn, η1,η2,…,ηn)定义辛内积,即上述Hermite内积的虚部〈x,y〉=

定义2若向量α,β的辛内积〈α,β〉=0,则称α与β辛正交,记为α⊥β;否则称α与β辛共轭.与欧式空间不同的是∀α均有〈α，α〉,则α⊥α,即辛空间中任一向量必与自身正交.

若向量组(α1,α2,…,αr,β1,β2,…,βr)(r≤n)满足:

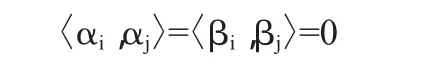
定理1[2]共轭辛正交向量组是线性无关向量组.

辛矩阵具有以下性质:

(1)其逆矩阵为辛矩阵;(2)其转置矩阵为辛矩阵;

(3)其行列式值为1或-1;(4)其乘积为辛矩阵.

定义4[3]一个2n阶矩阵B称为无穷小辛阵,如果满足JB+BTJ=0.若B为无穷小辛阵,则eB为辛阵;若C为对称阵,当且仅当B=JC时,则B为无穷小辛阵.

定义5若2n×2n矩阵H对任意2n维向量x,y有:＜x, Hy＞=＜y,Hx＞,则称H为Hamilton矩阵.易证Hamilton矩阵可等价定义为:(JH)T=JH或JHJ=HT.

定理2若u为Hamilton矩阵H的本征值,重数为m,则-u也是其本征值,重数也是m;若Hamilton矩阵H具有零本征值,则其重数为偶数.称本征值±u为Hamilton矩阵的互为辛共轭本征值,零本征值是特殊的辛本征值,与其自身互为辛共轭.

1.2.1.2 成立在职培训管理组:由区护士长任组长,指定护理组长一对一带教;根据CSSD制定的岗前培训计划,专人负责,落实到位。

定理4设±u≠0为Hamilton矩阵H的本征值,重数为m，则必存在共轭辛正交的向量组(ψ(0),ψ(1),…,ψ(m-1),φ(m-1),…, φ(1),φ(0)),即:

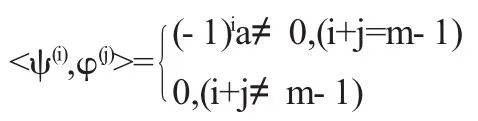
其中(ψ(0),ψ(1),…,ψ(m-1))和(φ(0),φ(1),…,φ(m-1))分别为u和-u对应的基本本征向量和Jordan型本征向量.

2 辛算法的构造

下面我们考虑一般的线性Hamilton体系,p=[p1,p2,…,pn]T, q=[q1,q2,…,qn]T,则,设Hamilton函数是H(z1,其中Z=[p,q]T=[z1,z2,…,z2n],C为

2n阶对称矩阵,即CT=C,则

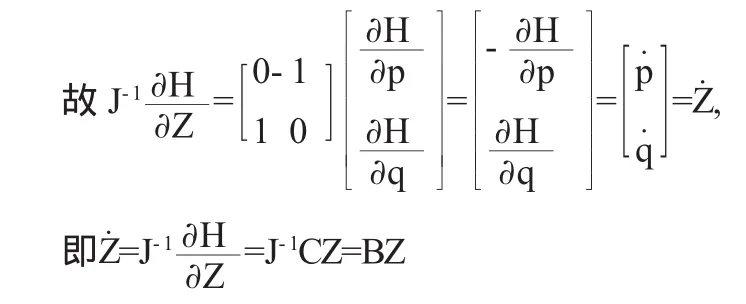
其中B=J-1C为无穷小辛阵,用分离变量法求得方程Z˙ =BZ的解为Z(0),求数值解时需要进行离散化,对变量t取步长为τ＞0,将连续依赖t的Z(t)离散化为{Z(kτ)},k=0,1,2,…则eBτZ(kτ),k=0,1,2,…下面我们利用有理Padé逼近构造eBτ保持典则变换的近似表达式,即用有理分式来逼近eBτ,其中Pm(x),Qn(x)分别为m,n次多项式.

定理5设B为2n阶矩阵,满足JB+BTJ=0,即B为无穷小辛阵,若的Padé逼近,则是算子etB保持为辛算法的近似表达式.

则2阶精度的辛差分格式(隐式)为:Z((k+1)τ)=Z(kτ)+Bτ 2 (Z((k+1)τ)+Z(kτ)).

下面讨论用分离变量法求解:Z˙=BZ,设Z(t)=ξ(t)ψ,其中ψ= (ψ1,ψ2,…,ψ2n)T与t无关,ξ(t)是t的函数,与向量ψ中的任何分量无关.则:Z˙=ξ˙(t)ψ=Bξ（t）ψ,故:得:Bψ=μψ,ξ(t) =eμt,而Bψ=μψ为Hamilton矩阵的本征问题.

于是:(B-μI)ψ=0,det(B-μI)=f(μ)=0,

故:f(H)=μ2nH2n+…+μ0I2n=0得:μi:ψ1,…,ψni

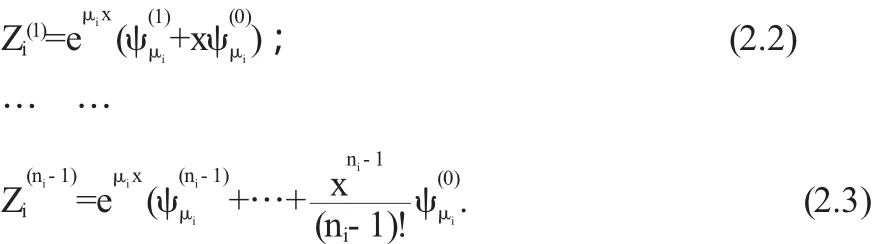
3 一个例子

易证:JHJ=HT,H为Hamilton矩阵.

且通过特征多项式求得其特征值为1重根,由分离变量法理论得知仅有上(2.1)式存在.

下面是辛算法(右图)和分离变量法(左图)求解x方向的结果:

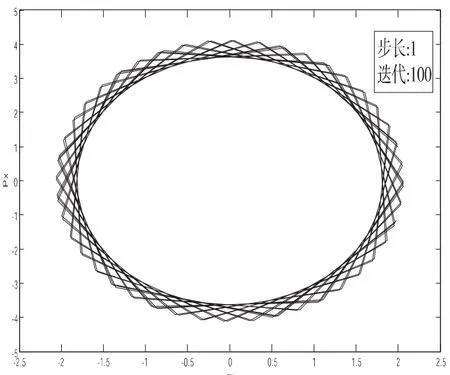
分离变量X·方向相图

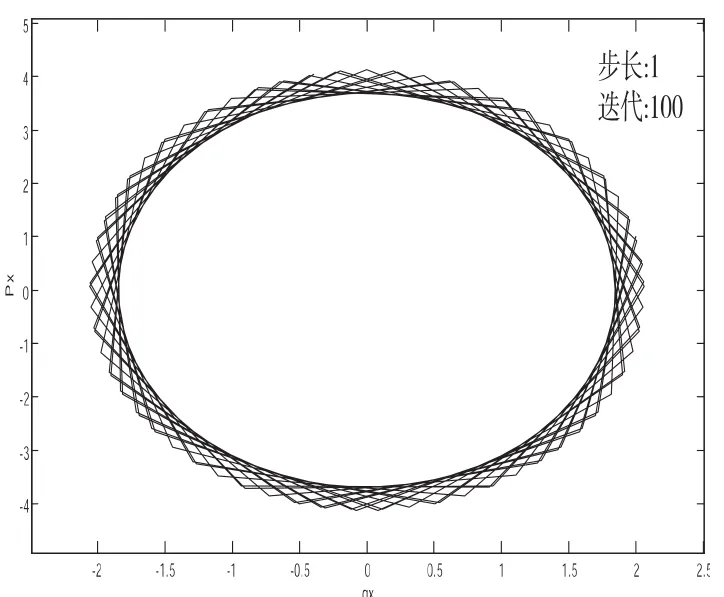
平面简谐振子X·方向相图

我们模拟了y方向步长为1的相图.此时的辛算法求得的结果与精确结果相差比较大,由于篇幅的原因这里就不再赘述了(有兴趣的读者可以参考我们的matlab程序).

function[ZZ]=Z(k,t,beta,z)

m=length(beta);

A=eye(m)-(t.*beta./2);

ZZ(:,1)=z;

fori=1:k

z=A(eye(m)+(t.*beta./2))*z;

ZZ(:,i+1)=z;

end

function[QQ]=FLBL(G,D,V)

fort=0:0.1:100

k=t*10+1;k=int64(k);

QQ(k,:)=G*[exp(D(1,1)*t)000;

0exp(D(2,2)*t)00;

00exp(D(3,3)*t)0;

000exp(D(4,4)*t)]*V;

end

下图为分离变量法和辛算法求解y方向的结果(此图的步长为0.1):

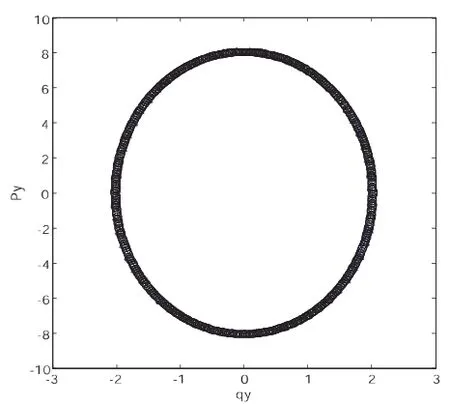
分离变量与辛算法组合图

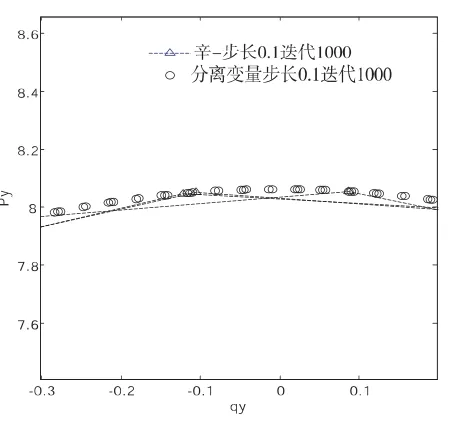
分离变量与辛算法比较图

从图上可以得出:用辛算法得到的解和用分离变量法得到的解几乎一致.

辛算法保持了Hamilton体系的两个守恒[4]:

（1）相空间体积的不变——Liouville-Poincaré守恒律ö

（2）运动不变量:如能量,动量,角动量的守恒

辛算法能够在数值计算中保持辛变换的结构,于是就会得到高的稳定性,辛算法的差分方法被认为是目前最稳定,高效的计算方法,适合用于经典力学体系.

我们知道,辛算法之所以逼近真实解的程度这么高是因为它的每一步迭代过程都保持了辛变换即典则变换,也就是说每次迭代都是能量守恒的.但是,19世纪庞加莱等人指出三体问题不可积,并意识到许多Hamilton系统是不可积的.其实并不是所有系统都是能量守恒的,耗散结构以及其他的动力系统都是实实在在存在的.但即便如此,Hamilton系统依旧是研究其他问题的重要体系.上世纪30年代,伟大的量子力学创始人之一Schrödinger先生就曾经说过“Hamilton原理已经成为现代物理学的基石”.所以,研究辛空间以及辛算法都是非常有价值的.

〔1〕李世雄.波动方程的高频近似与辛几何[M].北京:科学出版社，2001.3.

〔2〕姚伟岸,钟万勰.辛弹性力学[M].北京:高等教育出版社. 2002.4.

〔3〕秦孟兆.辛几何及计算哈密顿力学[J].力学与实践，1990（2）.

〔4〕冯康,秦孟兆.哈密儿顿系统的辛几何算法[M].杭州：浙江科学技术出版社，2003.

O241

A

1673-260X（2013）06-0006-03