创设问题情境，激发学生思维

张胜欣

摘 要： 本文是一节课的教学案例，作者从理论与实践相结合的角度展现了一节课的具体过程，通过创设相关的问题情境，引导学生合作探究，并针对过程中的精彩之处加以剖析，体现了课改给课堂带来的生机与活力。

关键词： 问题情境 合作探究 讨论交流 发现总结

苏霍姆林斯基说：“你要尽量使你们的学生看到、感觉到、触摸到他们不懂的东西，使他们面前出现疑问，如果你能做到这一点，事情就成功了一半。”这就需要教师对教学过程进行精心设计，创设各种教学情境，以此激发学生的学习动机和好奇心，激活学生的思维，使学生变“被动”为“主动”，变“苦学”为“乐学”，变“学会”为“会学”。下面是一节几何课的摘录：

在学完三角形全等的判定一后，继而要学习三角形全等的判定二时，我并没有根据教学大纲的编排程序进行教学，而是向学生提出这样一个富有挑战性的问题：

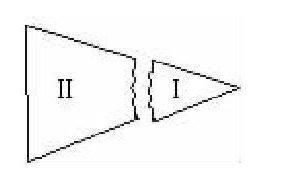
有一块三角形玻璃，由于不小心被折断成两块。如图，若根据需要必须到较远的地方玻璃厂复制一块与原来一样的三角形玻璃，试问你要怎么办？

（很多同学回答：把折断的两块玻璃带去，然后按原来模样重新制作一块。）

针对学生的回答，我先给予肯定，然后又给学生限定条件：若玻璃很大，路途遥远，只能允许带去一块，你又如何选择？

（这时学生在小组中纷纷议论起来，课堂气氛也因此达到高潮。）

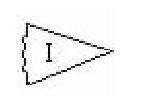
一会儿，第二小组有一位同学站起来回答道：应带Ⅰ去，如图，这一块有“两条边及其夹角”，可以根据我们上节课所学习的“SAS公理”，找到一个与它全等的三角形，再确定比例尺，就可以复制出一块与原来完全一样的三角形玻璃。

（我对他的说理加以表扬，并问其他同学是否同意他的观点。）

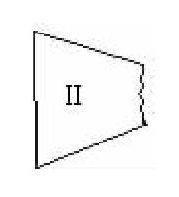
这时第四组有一位同学站起来反驳道：“按你的说法没错，只是你已知一个角，但这个角的两边你是怎么确定的？”刚才那位同学听了这一问，顿时醒悟过来，有点不服输地坐下去。这位同学继续说：我们小组讨论后认为应带Ⅱ去（如图）。其他组的同学追问：“为什么？”这位同学抓了抓脑袋回答说：“凭我们的感觉。”

（此时，全班学生笑了起来，整个课堂充满着欢乐的气氛。）

笑声之后，又有一位同学站了起来说：“应带Ⅱ去，因为Ⅱ的玻璃有两个角和一条公共边，另外两边被折断，但它们不平行，把它们延长必相交，这样可以找到与原来完全重合的三角形，从而确定比例就可以复制出与原来一模一样的三角形玻璃。

（对他的回答，很多同學投去了佩服的目光，我对他的回答也加以肯定。）

我继续追问：能否进一步用数学知识解释这个问题？

有一位同学立即回答：两个三角形若有两个角和这两个角的夹边对应相等，那么这两个三角形全等。

教师：这位同学的回答是否正确，我们先做完下面实验再来评价。要求按以下步骤作图：

1.先在一张纸上任作一个△ABC，然后在另一张纸上作线段A′B′=AB。

2.在A′B′的同旁分别以A′、B′为顶点，作∠MA′B′=∠A，∠NB′A′=∠B，A′M与B′N交于点C′，得△A′B′C′。

3.剪下△A′B′C′，放到△ABC上，你可以发现什么结论？

每位学生都开始积极实践，回答都是△ABC与△A′B′C′能完全重合在一起，即△ABC与△A′B′C′全等。这样刚才那位同学回答的正确性已经不讲自明了，对刚才只带Ⅱ就可以复制与原来一模一样的三角形玻璃也既知其然又知其所以然。

我继续提问：谁能给刚才这个结论定个名称？

（大部分同学举手。）

一个平时基础较差的同学站起来回答：把它称为“角边角公理”，用数学式子表示为“ASA”。

（我及时给予表扬，从该同学得意的神情可以看出他获得了成功的喜悦。）

语音刚落，又有一位同学站起来问道：“边角边公理”一定要求夹角，那么“角边角公理”是否也一定要两角夹边？

（被他这一问，全班一片寂静。）

我进一步引导：这个问题很精辟，如果两个三角形有两个和任意一条边相等，那么这两个三角形是否都全等，大家可以根据刚才的实验过程进行验证。

（各小组又忙了起来，纷纷画图，剪纸，结果都发现能完全重合在一起。）

这时一位女同学大胆站起来说：我不把它叫“角边角公理”，而要把它叫“角角边公理”。另一个男同学争着说：不对，应叫“边角角公理”。

看到学生激烈讨论的场面，我只开了一句玩笑：你们以后一个当婆婆，一个当公公，所以公说公有理，婆说婆有理，就让别人来评评理。

（全班哄堂大笑，学生没有苦学的压力。）

这时科代表站起来总结说：他们说得都对，两个三角形只要有两个角和任意一条边对应相等，它们就全等，即“ASA”“AAS”“SAA”都是正确的。

而后我也作了小结：今天我们所要学习的主要内容，刚才我们的科代表都总结、归纳了，还有哪位同学有疑问吗？

这时又有一位同学站起来问：我们现在知道有“SAS公理”，“ASA公理”，“AAS公理”，“SAA公理”，那么是否还有“AA公理”，“SS公理”，“AAA公理”，“SSS公理”呢？（此时下课铃声响起。）

我投去了佩服的目光，简单地回答：这位同学提出的问题令我大吃一惊，他实在太厉害了，由于时间问题，这个问题只能留给大家课外继续探讨。

本节课主要采用了“问题—探究”型的教学模式，通过“问题情境—合作探究—讨论交流—实践发现”这几个数学活动，把静态知识转化为动态的探索对象，贯穿了“育人为本”的数学思想，为学生营造了一种愉悦、和谐、自主的课堂气氛，改变了传统单一的教学模式。通过这堂课的教学，我看到了学生自己参与探索知识形成过程获得成功后的喜悦和自豪，以及对学习数学的信心，深深体会到不仅要教给学生知识，还要重视教育学生敢于追求真理，探索真理，发展真理，使学生各方面的能力在教学中得到培养和提高。