有效利用变式教学，成就数学高效课堂

贺卫星

摘 要：针对数学课堂、数学知识的特点，对课堂中的例题或习题进行评讲时，采用变式教学，能够帮助学生梳理数学知识并延伸知识的深度与广度，一题多解可以发散学生的思维，使数学课堂更加高效。

关键词：一题多变；一题多解；高效课堂

高效课堂是指在有效课堂的基础上，完成教学任务和达到教学目标的效率较高、效果较好的课堂。利用变式教学在教学中适当的一题多变，可以激发学生去发现和去创造的强烈欲望，加深学生对所学知识的深刻理解，训练学生对数学思想和数学方法的娴熟运用，锻炼学生思维的广阔性、深刻性、灵活性和独创性，从而培养学生的思维品质，发展学生的创造性思维。引导学生从“变”中发现“不变”的本质，从而吃透例题习题，回归课本。

一、一题多变，培养学生的思维能力

在课堂教学中，数学题型众多，把部分类型相同，考查的知识点相同的题目归类对比呈现，在例题讲解时，变换题目的题设或结论，可以让学生在较短的时间内掌握同类型的习题，让学生更容易理解知识的内在联系。

1.改变题设，挖掘习题含量

例1.顺次连接任意四边形各边中点组成的新的四边形是什么四边形？为什么？

可将题设部分变为：

变式1：顺次连接矩形各边中点组成的新的四边形是什么四边形？

变式2：顺次连接菱形各边中点组成的新的四边形是什么四边形？

变式3：顺次连接对角线互相垂直的四边形各边中点组成的新的四边形是什么四边形？

变式4：顺次连接对角线相等的四边形各边中点组成的新的四边形是什么四边形？

变式5：顺次连接对角线互相垂直且相等的四边形各边中点组成的新的四边形是什么四边形？

变式6：顺次连接正方形各边中点组成的新的四边形是什么四边形？

……

引导学生探究不同四边形的中点四边形，可以让学生熟悉特殊四边形的判定和性质。这样利用一道例题的教学，就可以实现整章知识中平行四边形、矩形、菱形、正方形的性质和判定以及中位线等知识的系统梳理，达到高效课堂的目的。

2.简化题设，可以让学生更容易理解题意，感悟数学的内在联系，形成数学思想方法

例2.两工程队参与一项筑路工程，甲队单独施工1个月可以完成总工程的三分之一，这时增加了乙队又共同工作了半个月，总工程全部完成，哪个队的施工速度快？（学生第一次接触感觉很难，已知条件难以理解，可以把题设做些更换，帮助他们由易到难地理解题意，掌握此种类型题目的解法）

变式：两工程队参与一项筑路工程，甲队单独施工3个月可以完成，这时如果甲队单独施工一个半月，再由乙队单独施工半个月可将总工程全部完成，哪个队的施工速度快？

这样，学生可以尽快地理解应用题中的数量逻辑关系，提高课堂效率。

3.延伸题设，拓展题目的深度

比如一道中考题：

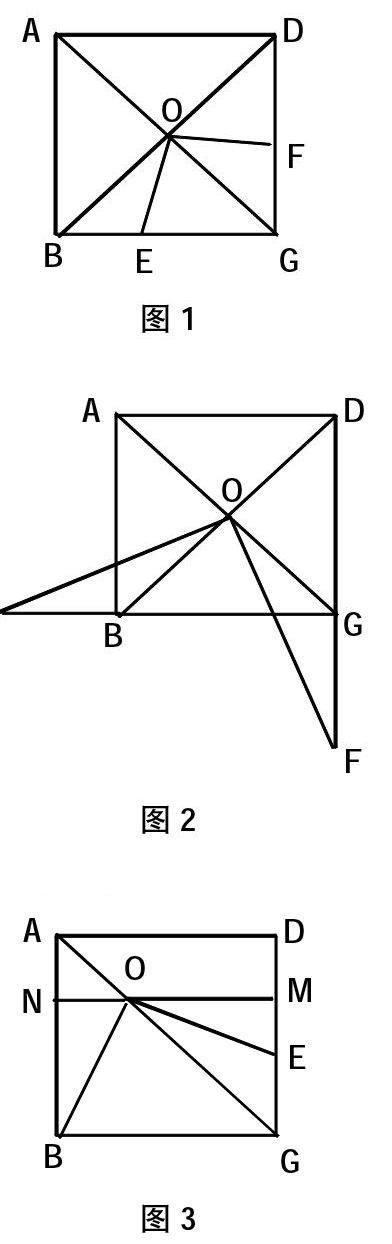
例3.如图1，已知正方形ABCD，∠EOF=90°，O是对角线交点，点E，F在BC，CD上，求证EO=FO。

通过利用正方形的性质，以及∠EOF=90°可以证明△BOE≌△COF，从而得到EO=FO题目较容易。

如果将已知条件延伸，可以拓展为一个动点问题：

变式一：如图2，已知正方形ABCD，∠EOF=90°，O是对角线交点，点E，F在BC，CD边延长线上，求证EO=FO。

证明：∵四边形ABCD是正方形，

∴BO=CO，∠BOC=90°，∠OBE=∠OCF

又∵∠EOF=90°

∴∠BOE=∠COF，∴△BOE≌△COF，∴EO=FO

变式二：如图3，已知正方形ABCD，O是AC上任意一点，∠BOE=90°，点E在BC边上，求证BO=EO。

解法：过O作ON，OM⊥AB，DC

∵四边形ABCD是正方形

∴∠OCM=45°

又∵ON，OM⊥AB，DC

∴MO=CM=NB

∴∠ONB=∠OMC，∠MOE=∠NBO

∴△MOE≌△NBO

∴BO=EO

这样一道题目延伸为需要运用运动的观点方法解决较难的综合题，从而拓展了题目的深度，提高了课堂效率。

4.变结论，可以是简化结论使学生更容易解决问题，也可深化结论防止学生对所学的基础知识和已掌握的基本技能陷于僵化，所以在教学中可借变式帮助学生进行发散思维的训练

例4.在原题基础上引申，加深对所学知识的理解和掌握。例如，一家商店将某种服装按成本价提高40%后标价，又以八折优惠卖出，结果每件仍获利15元。这种服装每件的成本是多少元？

解：设每件服装的成本为x元，依题意得：

（1+40%）x·80%-x=15

解得x=125

变式一：一家商店将某种服装标价为175，以八折优惠卖出，结果每件仍获利15元。这种服装每件的成本价是多少元？

变式二：一家商店某种服装的成本价是125元，以八折优惠卖出，结果每件仍获利15元。这种服装每件的标价是多少元？

变式三：一家商店某种服装的成本价是125元，提高40%后标价，又以八折优惠卖出。这种服装每件获利多少元？

变式四：一家商店某种服装的成本价是125元，提高40%后标价，折价销售时，结果每件仍获利15元，这种服装每件是按几折销售的？

以上四个变式引申比较自然，有利于学生把知识学活，提高学生学习效率。

二、一题多解，拓宽解题思路

一题多解是从不同的视角、不同的方位审视分析同一问题中的数量、位置关系，用不同解法求得相同结果的思维过程。通过探求同一问题的不同解法，可以引出相关的多个知识点和解题方案，有助于培养学生的洞察力和思维的变通性、独创性，从而培养学生的创新思维的意识，提高课堂实效性。

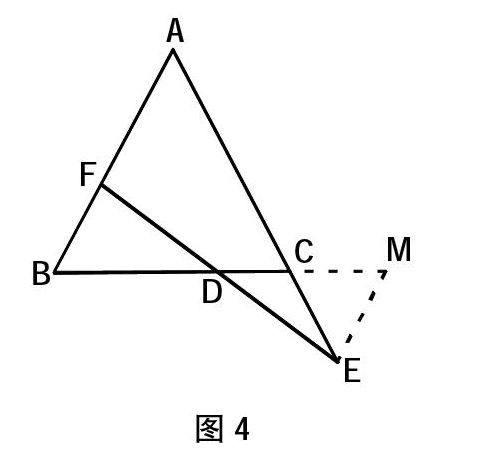
例5.已知AB=AC，E是AC延长线上一点，且有BF=CE，连接FE交BC于D。求证：FD=DE。

证法一：如图4

证明：过E点作EM∥AB交DC延长线于M点，则∠M=∠B，

又因为∠ACB=∠B，∠ACB=∠ECM=∠M，

所以CE=EM，

又EC=BF

从而EM=BF，∠BFD=∠DEM

则△DBF≌△DME，故FD=ED；

证法二：如图5

证明：过F点作FM∥AE，交BD于点M，

则∠1=∠2=∠B

所以BF=FM，

又∠4=∠3，∠5=∠E，BF=EC

所以△DMF≌△DCE，故FD=DE。

三、举一反三，培养学生思维的迁移能力

例6.平行四边形ABCD中AD=2AB，E、F在直线AB上，且AE=BF=AB，求证：DF⊥CE。

证法一：如图6，易知△ADF、△BCE为等腰三角形，

故∠1=∠F，∠2=∠E，

又CD∥AB，故∠3=∠F，∠4=∠E，

从而∠1=∠3，∠2=∠4，

而∠1+∠2+∠3+∠4=180°，故∠3+∠4=90°，所以∠COD=90°，所以DF⊥CE。

证法二：如图7，连接MN，则CD=BF，且CD∥BF，

故BFCD为平行四边形，则CN=BN=AB，

同理，DM=MA=AB，故CN=DM且CN∥DM，

得平行四边形CDMN，易见CD=DM，故CDMN也是菱形，根据菱形的对角线互相垂直，结论成立。

证法三：如图8，连接BM、AN，可证△AFN中，BN=BF=BA，则△AFN为直角三角形，即DF⊥AN，利用中位线定理可知AN∥CE，故DF⊥CE。

证法四：如图9，作DG∥CE交AE延长线于G，则EG=CD=AB=AE，故AD=AG=AF，从而DF⊥DG，而DG∥CE，故DF⊥CE。

总之，在数学课堂的例题或习题的讲解过程中，通过变式探索各种情况下问题的结论，是帮助学生培养探索能力和逻辑思维能力不可缺少的训练手段。并且，适当的变式教学是课堂教学艺术的一种表现形式，是活跃课堂气氛，调动学生积极性的一种有效途径，是促进学生进行联想、转化、探索、推理能力的一种主要手段。问题的变式一般具有启发性、强化性、巩固性等功能，能使学生对一些较高层次的数学方法和观念产生较强的感受，从而对所学知识掌握更牢靠，运用更灵活，最终达到提高课堂效率的目的。

参考文献：

王义秀，臧传军.新课程标准与课堂教学实践.北京师范大学出版社，2010-07.

（作者单位 广东省广州市番禺区石楼第二中学）