了解积分——求和

丁 韫， 杨晓春

（大连海事大学数学系，辽宁大连 116026）

1 黎曼和的困惑

求和是代数运算中最简单、也是最先遇到的一种运算.对有限个数的求和问题，一直被认为是解决的最彻底，也最叫人放心的，最简单的运算［1－4］.

然而，在黎曼积分的过程中我们也同样遇到了求和这样一个步骤，给我们带来的麻烦远远地超出了我们对有限个数求和问题难度的想象.

我们先看一下黎曼和的内容［5－10］.在引入黎曼积分时，总是给出一个数学上求曲边梯形面积的例子.在完成了分割、近似代替这两个步骤后，开始了对整个曲边梯形的近似估计，也就是做曲边梯形总面积A的近似值——将所有的小矩形的面积相加，作为曲边梯形A的近似代替——黎曼和

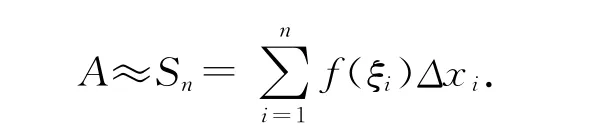
上面的这个黎曼和看起来与一般的有限个数求和没有什么不同，因为，求和中的每一项都是数.但是如果我们加上做这个和式的目的，情况就完全不同了.

由于一个曲边梯形的面积是一个客观存在的事实.当然这就要求，无论人们怎么来做这个面积的近似，如果这个近似值被大家认为是可以接受的，其最后得到的结果，必须只能是无限接近或直接等于一个值——面积的真值.换句话说，面积的值，应该不依赖于人们在求面积的过程中的个人行为或主观方式.

于是，上面的黎曼和中就出现了两个附加的要求：与闭区间［a，b］分割的方式无关，也与近似代替的方式无关，或者说，与矩形的高度，我们选择的f（ξi）无关（一般的教材中用的是与小区间［xi－1，xi］中ξi的选择无关）.这两个无关，在教材中被正面的表述为两个任意性.

从上面的内容里可以看出，黎曼和已经不是我们普通意义下的有限个数的简单求和了.它表现在几个方面的不同.首先求和中有一个游标n，加上由于要求求和与分割的方式无关，而分割的方式可以有无限多种，于是，求和的项数是不固定的不说，而且可能的求和结果，如果和分法相关的话，就有可能是无限个.其次，由于要求求和的结果也不依赖与f（ξi），而f（ξi）的取法也可以是无限多个，于是，黎曼和中的表面上的有限个数的求和，就成为了有限个“每一项都可能有无限多种变化的，而且项数本身也可有无限多种取法”的代数和.

简言之，就是变数外加变项数，求有限和，并希望和的值惟一确定.这种期望听起来都多少有些超凡脱俗.

如果抽象一些说的话，其实黎曼和是关于分点的个数，分割的方法，及f（ξi）取法的三元函数，即

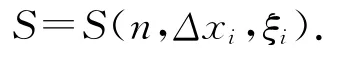
不仅如此，它关于后两者还是一个隐函数.对这样的问题，求出其代数和，并希望和为一个不依赖于分法也不依赖于函数值的取法的趋向于真值的确定的数，其困难是不言而喻的.

当然，这个面积引入，实际上也告知了两个前提，那就是曲边梯形的尺度是有限的，或者简单的说，其各个边长，特别是低和高都是有限的.这也就成了我们讨论黎曼积分的前提.

2 黎曼求和的处理

如上面所说，黎曼和的本质是“变数外加变项数，求有限和”.如果这些数之间没有必然的约束和逻辑联系，希望最后的结果能如期望的那样唯一确定，是很难实现的.

然而，黎曼和又是有别于一般的“变数外加变项数，求有限和”这个问题的.因为我们的目标是求一个曲边梯形的面积，而为了实现这一目标，我们必须对分割的过程逐步细化，均匀化.这样一来，当分割满足了这样的要求时，各个独立的分割之间的差别就不是十分的明显.换句话说，分割的差别，在起初分割的很粗的时候，或者说每一段小区间的长度是明显可见的时候，两种分割的差别会很大；当两种分割，都逐步细化，以至于每一个局部都小到“微乎其微”，虽然从分化的角度看，其差别依然很大，但是其对积分的贡献，就慢慢的趋同了.因为最终决定结果的，不仅仅是分化，而是分化后，并以这样的分割小区间作为支撑的小矩形作为局部近似代替后的整体和.每一个对应的小的局部，在求和的过程中表现的差异可以不同，但是整体的效果，通过局部差异之间的互补，可能得到很好的修正.这样说，在此基础上求出最后的精确值，是有成立的可能性和必然性的.

有了求和的可能性，如何实现？仅仅从认识的角度来看，出路也在于，尽可能把这里的内涵很丰富的求和问题，化为普通的有限个数字的代数和.

其实第一可积性定理的证明过程，就是这样一个转化的过程.首先，达布为我们做了两个特殊的和：达布大和σ大、达布小和σ小.这两个和有一个共同的特点，那就是它们已经与f（ξi）的取法无关了.其次，由于黎曼积分的要求还是在经典的意义下定义的，因此不包括广义函数，从而按照定义可以推得，可积的必要性为函数有界.这就保证了达布大和σ大、达布小和σ小是一个有界函数（这或许就是为什么起初一定要做一个形式上的有限和的原因吧，只有有限和才可以保证求和的结果是有界的）.再次，通过对达布大和σ大、达布小和σ小取下极限、上极限（或者下确界、上确界）来消除分割的影响，达到与分割无关的目的.具体地说，由于基于每种分法而构成的达布大和σ大、达布小和σ小所形成的数集也好，数列也好，都是有界的，因此其上极限（或者最大聚点）、下极限（最小聚点）都是存在的.这确保了上、下极限的存在，而由于这两个极限存在，则是唯一的，于是，无形中，分割的影响就被消除了.

有了上面的处理，加上黎曼和式介于达布大和σ大与达布小和σ小之间这一事实，以及极限的保号性，导致了黎曼和被夹在了两个数——达布大和σ大的下极限与达布小和σ小的上极限之间，而这两个数字本身都是唯一确定的.当然，黎曼和在任意的分割下，及函数值f（ξi）的任意取法下的结果，就被限制在一个区间所限定的范围之内，当这个范围缩小为一点时，黎曼和的值也就被确定下来了.

总的说来，求黎曼和的过程，就是一个如何化不确定的有限项求和问题，为一个相对确定的有限和，以及在此基础上的实数集合或序列具有的特有属性的问题.这种有机结的合处理的很是相得益彰，经典数学中也是不多见的.

3 一般积分中求和的条件和要求

黎曼和引入过程是一个直观可视的过程，大家接受起来还是很自然的.究其原因，黎曼积分的概念是建立在数域上的函数的前提之下的，因此，里面的四则运算都是可行的.

但是对于一般的集合上，如果也想做积分，也想通过微元法这样的步骤来实现，需要考虑的问题就会更加的复杂.

首先我们要面临的，就是运算问题，我们必须在集合上建立起可行的加法运算及乘法运算（最起码也得有数乘运算），使之满足要求.

处理这样的问题直接可以想到的大约有两种，其一是，在集合上面建立一种规则，使得元素在这个规则下都可以数量化，从而使得集合这样抽象的“体”，本身也可以进行量度.其二，在集合上直接建立一种新的可以称之为加法的运算，使其完全保持有数字之间的加法做代数运算时，所满足的各种运算规则.

显然，后一种想法过于理想化，在一般的情况下很难实现；而前一种思维方式，在数学中使用的相对较多.

如果从黎曼积分求和的几何意义上看，无非是用局部规则的可求面积的矩形、梯形或者多边形，来近似地代替整个曲边梯形而已，或者说用规则的几何图形来覆盖曲边的梯形.从这个角度上看，这种覆盖应该具有两个基本特点：就是在任何局部都不能重复覆盖；而整体覆盖，在图形的内部又不能有任何裸露的地方，且在顶部仅仅有极小的误差.

这样说来，做一个不规则的曲边图形的覆盖，就不一定要按照确定的前后顺序来覆盖，可以，一片片独立地各自覆盖，只要保证这种覆盖具有了上面提到的两点要求即可.于是，在实变函数中，就积分的问题中的求和，就采用了这样的思想，换了一种思路来覆盖：不去从定义域着手，而是从值域着手，然后根据值域的需求，去独立地找到支撑这些函数值的各自支撑区间，同样实现了覆盖的目的.当然，实变函数并不是彻彻底底地在集合上建立积分的.因为，在建立积分的时候，其落脚点依然是在区间上，而不是集合上，不过处理的方法，是从处理一般集合的观点出发罢了.当然，量度一个区间的方法，发生了极大的而变化，不是用我们熟悉的区间，取代它的是另外一种称之为测度的工具.

如我们所知，函数论中讨论的对象主要是函数，特别是研究积分这样的运算，都是对函数而言，因此，被积的对象，基本上被限定数这个范围里面了.能够变化的，就是支撑函数的基——我们通常称作的定义域或更一般的定义集.关于定义集的要求，我们已经在此序列文中的前两篇讨论‘分割’、‘近似代替’中，做了一些说明，这里就不重复［11－12］.

4 有限和与无限和

翻开数学分析或者高等数学的教材，关于黎曼和的描述，都是谓之曰：有限和.从求和的表达式上看，其特征的确是如此.然而，细细想来，由于如前面所说的分割需要有任意性、均匀性、以及局部要小到“微乎其微”，那么求和的项数就是一个不确定的数了.而且这个数要多大，就得有多大，其实它已经具备了无穷大的特征.

对无限多个数的求和问题，在高等数学和数学分析中都有专门的讨论，也就是数项级数部分所讲述的内容.这里为什么不直接把求和视为一个无穷求和问题呢？无论出于什么原因，起码，这样处理的好处是避免了一个问题，就是无穷多的数求和的收敛性问题.因为无穷多个元素求和，其和是不能确定的，等不等于一个有限的数，本身就不能保证.即使是每一项都是无穷小量，无穷多个元素合起来，依然可以是一个无穷大量.所以，不能直接按照无穷求和来处理，而是把一个事实上无穷求和的问题，分解成了变项数的有限求和，外加对项数求极限的问题.

仔细想想，这中间的处理是否有遗漏，还是一个值得思考的问题，因为对于一个闭区间的任意分法，可以有不可数无限种，而后来求极限的运载参数n是一个可数的无穷大量，这中间逻辑上似乎有些不匹配.如果理解成分法是不可数无限多个，而每一种分法都只有至多可数个分点的话（此时，可以是有限和＋n趋近于无穷大的情形），当然现行的做法，也不无不可.

这种思想后来被沿用到了级数的处理，其处理过程也是，把一个无穷求和的问题分拆成了两步：第一步，求一个有限部分和（前n项）；第二部，对项数求极限，也即，令项数趋于无穷.在这样处理的方式下，建立起了整个的级数理论.

这样处理，虽然可以简单地解决无穷求和问题或者是‘无穷’问题［13］，但是也有留下许多的问题值得我们思考，对项目数n取趋于无穷大的极限，是否涵盖了原问题中的所有可能出现的情形和状况？是否有遗漏？

回顾前面有关无穷大的定义，我们也知道，实际上无穷大量是一个动态的过程，而非一个固定的值.然而，无穷大到底是什么？应该如何看待？事实上，在如何对待无穷大量这个特殊的数学量的研讨上，本身就是一个近两百年来一直无法得到统一看法的事情.因此，用极限这个运载工具，来建立有限和无限的联系，是否逻辑上很严谨，还值得深入的研究.

5 感 受

求和问题本来是一个简单的问题，但是撰写这部分内容的时候，居然反复修改，花了很多的时间，也落下了这许多的文字，自己读后，依然是觉得有许多话想说，但有如什么东西哽嗓噎喉般，不说很难受，但是又找不到合适的言语说清楚，故而，有说出来更难受的感觉.

有限和无限这一对相对立又统一的孪生的矛盾体，总是给我们带来诸多遐想，给了我们无限的发挥自己能力的空间，但也同时受到人们只能从事于有限行为这样一种行为方式的限制，无法踏足于无限空间的每一个角落，因此，是否有所遗漏，只能是从逻辑上去证实.然而，逻辑本身是有死角和盲区的，中间本身就存在着各种悖论，无法释然这大千世界的各种现象也就不足为奇了.

［1］克莱因 M.古今数学思想［M］.上海：上海科学技术出版社，1979.

［2］齐民有.重温微积分［M］.北京：高等教育出版社，2004.

［3］约翰L卡斯蒂.20世纪数学的五大指导理论［M］.上海：上海教育出版社，2000.

［4］徐宗本.从大学数学走向现代数学［M］.北京：科学出版社，2007.

［5］吉林大学数学系.数学分析［M］.北京：人民教育出版社，1977.

［6］武汉大学数学系.数学分析［M］.北京：人民教育出版社，1978.

［7］华中师范大学数学系.数学分析［M］.北京：高等教育出版社，1981.

［8］复旦大学数学系.数学分析［M］.上海：上海科学技术出版社，1979.

［9］菲赫金哥尔茨 ΓΜ.微积分学教程［M］.北京：人民教育出版社，1981.

［10］同济大学应用数学系.高等数学［M］.北京：高等教育出版社，2001.

［11］杨晓春，丁韫.漫谈数学发展及其与社会发展的关系［M］.大学数学，2005，21（3），：136－140.

［12］丁韫，杨晓春.了解积分——由积分的概念所想到的问题［M］.大学数学，2010，26（4）：181－186.

［13］鲁丁 W.实分析与复分析 ［M］.北京：高等教育出版社，1988.