一致有界树指标马氏链的层频率的强大数定律

曹芳芳

（江苏大学理学院，镇江 212013）

1 引 言

树图G=｛T，E｝ 是一个没有回路的连通树图，对于任意两个顶点α≠β∈T，设αβ是连接α与β的唯一路径，路径中含有的边数记为d（α，β） ，称为α到β的距离.设T为局部有限无穷树，选择一个顶点作为根点，记为o.当T中每个顶点的度是一致有界时，称T为一致有界树.若T上的每个顶点都有M＋1（M为正整数）个相邻顶点，称之为Bethe树，记作TB，M.另外还有一种树叫Cayley树，记作TC，M.在TC，M上，根顶点有M个相邻顶点，而其他顶点有M＋1个相邻顶点.这是两种常见的齐次树.显然这两种齐次树是一致有界树的特例.

设T是一无限树，｛Nn，n≥1｝ 是一列正整数.如果一个顶点到根顶点的距离为n，则称此顶点为n层上的顶点.若第n层 （n≥ 1 ） 上每个顶点与第n＋1层上的Nn＋1个顶点相邻，则称T为广义Bethe树和广义Cayley树.规定N0＝1.若当n为奇数时，Nn＋1＝2，当n为偶数时，Nn＋1＝3，则称这样定义的树为TC（2，3） 奇偶树.显然TC（2，3） 奇偶树也是一致有界树的特例.在不引起混淆的情形下，本文中将一致有界树简记为T.

在树图T中，称n层上所有顶点的集合为T的第n代，记为Ln.用T（n）表示T的前n代顶点全体构成的子集.记顶点t的第1代祖先为1t，第2代祖先记为2t，依此类推，记其第n代祖先为nt.对于树T上的任意两个顶点s和t，如果s位于从根顶点o到t的唯一路径上，记s≤t.用s∧t表示

为S2上的随机矩阵，如果对于任何顶点t，

树图模型近年来已经引起了物理学、概率论及信息论界的广泛兴趣.Benjamini和Peres引进了树指标马氏链的概念，并研究其常返性和射线常返性［1］.之后叶中行与Berger又研究了树上PPG不变及遍历随机场的Shannon－McMillan定理［2］，不过其收敛是依概率收敛.近年来，杨卫国研究了齐次树上有限齐次马氏链的强大数定律和渐进均分性（AEP）［3］.杨卫国，黄辉林和马越研究了奇偶树上马氏链场的强大数定律［4］.黄辉林和杨卫国研究了一致有界树指标马氏链的强大数定律［5］.潘恒和杨卫国研究了Cayley树图上奇偶马氏链场的强极限定理［6］.本文利用一致有界树指标马氏链的强大数定律，给出一致有界树指标马氏链的层频率的强大数定律.

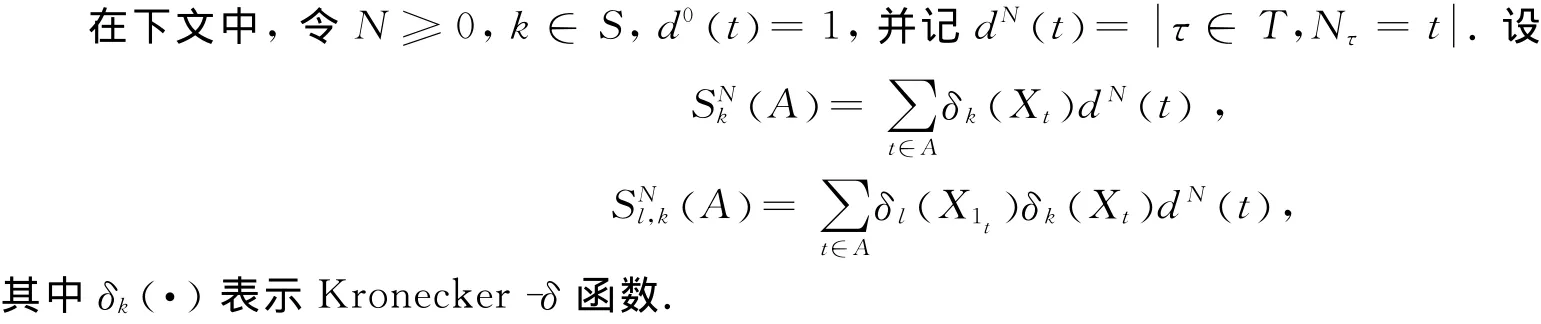
2 主要结果

证 在定理2中取N＝0即可得到（12）式.

［1］Benjamini I，Peres Y.Markov chains indexed by trees［J］.Ann.Probab.，1994，22：219－243.

［2］Ye Z，Berger T.Ergodic，regulary and asymptotic equipartition property of random fields on trees［J］.Combine Inform System Sci，1996，21：157－184.

［3］Yang W G..Some limit properties for markov chains indexed by a homogeneous tree.Statist［J］.Probab.，Lett.，2003，65：241－250.

［4］杨卫国，黄辉林，马越.奇偶树上马氏链场的强大数定律［J］.江苏大学学报，2005，26：243－247.

［5］Huang H L，Yang W G..Strong law of large numbers for markov chains indexed by an infinite tree with uniformly bounded degree［J］.Science In China Series A：Mathematics.，2008，51：161－320.

［6］潘恒，杨卫国.Cayley树图上奇偶马氏链场的强极限定理［J］.应用概率统计，2011，27：22－28.