《高等数学》中的“爱尔兰根纲领”及其应用

张冬燕， 刘缵武， 孙铭娟

（解放军信息工程大学理学院，河南郑州 450000）

1 引 言

匈牙利数学家路莎·彼得说：“数学中最主要的成分始终是思想方法，而这确实是人类共同的思想源泉，即使作家或艺术家也可从中汲取营养.”［1］诚如其言，数学思想方法是数学知识的精髓和灵魂，学习数学从某种意义上讲就是要获得用以指导工作和生活的数学的思想和方法.因此，深入探究和挖掘数学各门学科所蕴含的数学思想方法，并在教学中注重这些思想方法的渗透，对培养学生的数学意识，提升他们的数学素养具有重要意义.

高等数学是理工科院校普遍开始的一门公共基础课，它内容丰富，影响面广，蕴含了许多重要的数学思想方法，对此不少学者都曾进行过详细总结［2－4］.但是，人们从高等数学里梳理出的种种思想方法中，有一种数学思想却鲜为人注意，它就是著名的“爱尔兰根纲领”所阐述的几何不变量思想.

“爱尔兰根纲领”系指：《关于现代几何学研究的比较考察—1872年在爱尔兰根大学评议会及哲学院开学典礼上提出的纲要》.这是德国大数学家克莱因（Felix Klein）为其教授就职发表的一篇著名演说，因文中首次提出了统一几何学的纲领性结论，而被世人称为“爱尔兰根纲领”.在纲领中，克莱因认为每一种几何学都对应一个变换群，几何学所要做的就是研究某种变换群下的几何不变量.按照这个观点，我们研究几何图形，其实就是研究图形在某种变换群下的那些不变的性质和量以及保持这些性质不变的变换.这种以变换群为工具讨论几何学的思想，化静为动，将当时所有的几何学都统一了起来，并由此引领了其后50年间几何学家的研究方向，对数学的发展尤其是几何、群论的发展产生了深远影响，同时还对物理学尤其是狭义相对论产生了积极影响.

2 《高等数学》中的“爱尔兰根纲领”思想

时至今日，“爱尔兰根纲领”虽然已不能涵盖所有的几何学，但它所阐述的不变量思想仍是数学史上一笔宝贵的思想财富.在高等数学教学中，如能结合相关内容，适时介绍、渗透这种思想，对开阔学生视野，提升对几何更高层次上的认识，以及对学生后续物理等课程的学习都大有裨益.那么高等数学中哪些内容体现了“爱尔兰根纲领”的思想呢？

典型案例一是利用伸缩变换，由特殊二次曲面的方程和形状推导一般二次曲面的标准方程和形状.在高等数学教材［5］中，讨论一般二次曲面方程时介绍了将几何图形伸缩变形的方法：在xOy面上，把点M（x，y）变为点M′（x，λy），从而把点M的轨迹C变为点M′的轨迹C′，称为把图形C沿y轴方向伸缩λ倍变成图形C′.这里通过伸缩变形将一种图形变成另一个几何图形的过程就是伸缩变换.在伸缩变换下，几何图形的形状、面积、体积等性质都发生了变化，但值得注意的是，有些几何特性在伸缩变换下却具有不变性，如图形上点与曲线的结合关系不变，点在曲线上的顺序不变.这就使得图形上共线点变为共线点，共点线变为共点线，而且点与点、线与线之间的相对位置保持不变.于是，借助伸缩变换下的这些不变性，我们就可以由特殊到一般，将空间中的椭球面、椭圆锥面、椭圆抛物面等分别看作是球面、圆锥面、旋转抛物面等特殊曲面的伸缩变形，进而根据伸缩变形中曲面方程未知量的变化规律，推导出一般二次曲面的标准方程.

典型案例二是利用伸缩变形中物体质量的不变性推导物体的质心和转动惯量的计算公式.质心和转动惯量是物理学中的两个重要概念，在重积分应用一节中，教材［6］利用积分元素法来求它们的计算公式.将物体分割成有限个小物体，由于每个小物体的质量分布近似均匀，且在压缩变形中质量保持不变，因此每个小物体的质量可想象成浓缩到物体内的一点上，于是求整个物体质心和转动惯量时，就可把整个物体视为是由有限个质点所构成的质点系来处理.上述过程中，利用变形下物体质量的不变性，把物体抽象成有限质点系，巧妙实现了无限与有限的转化，这是物理学上解决问题的一种常用方法.

事实上，在高等数学教材中，除以上两处体现了“变换下的不变量”思想外，还有很多内容蕴含着这种思想，现在我们举例说明它在高等数学中的应用.

3 “爱尔兰根纲领”的不变量思想在积分学中的应用

首先我们给出有关旋转体体积和表面积的简单计算方法.

定理1 设旋转体（如图1所示）由xOy坐标面上的图形A绕坐标轴x轴（或y轴）旋转一周而成，如果图形A的质心为（¯x，¯y），面积为S，则该旋转体的体积

证 体密度μ＝1的物体的体积在数值上等于它的质量M.为此，视所求旋转体为体密度μ＝1的物体，求旋转体的体积就相当于求该物体的质量.由已知，旋转体由平面图形A绕坐标轴x轴（或y轴）一周无限叠加而成.把面A看成一张薄片，它的质量m＝μ·S＝S.想象把薄片A浓缩成一个点，浓缩到它的质心点上，使质量全部集中于它的质心），这样利用伸缩变换，旋转体就变成了由质量为S的质点A绕x轴（或y轴）旋转而成的一条圆心在x轴（或y轴）上，半径为（或）的圆链.圆链的线密度ρ＝m＝S，所以圆链的质量，从而旋转体的体积

这个定理实际是著名的帕普斯—古尔丁定理，国内很多学者曾给出过它的证明［7］.这里我们另辟蹊径，采用不变量思想，抓住物体在伸缩变换下的质量不变性，把物体变形为“链条”，再根据质量与体积的转化关系求出旋转体的体积.

用类似的方法还可求旋转体的表面积.旋转体的表面可看作一张由曲线C（如图1）绕x轴旋转一周织成的面密度为1的网面，若设）为曲线C的质心，L为C的弧长，想象把该网面浓缩为一条线密度为L的细丝，则它的质量也即旋转体的表面积S＝·L.由此得：

定理2 设旋转体由xOy坐标面上的以连续曲线C为曲边的图形A绕坐标轴x轴（或y轴）旋转一周而成，如果曲线C的质心为（），弧长为L，则该旋转体的表面积为S＝·L.

下面再举两个用“爱尔兰根纲领”的不变量思想解题的例子.

例1［8］求星形线x＝acos3θ，y＝asin3θ所围图形D的面积.

分析 正如伸缩变形不会改变图形各部分位置的相对次序，对图形作非线性的扭曲、拉伸变形（不包括撕开、接合），图形各部分位置的相对次序仍然保持不变，为此，我们设想星形线所围图形D由圆面经拉伸变形而来，若能找到变形前后图形面积的变化规律，就可利用圆的面积来求解未知面积.

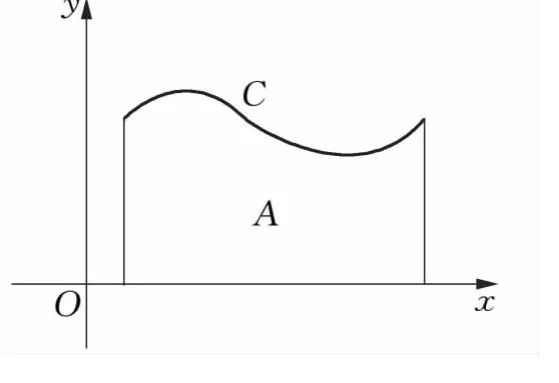
图1

解 作变换

则有w2＋v2＝1.变换（1）可看作从直角坐标平面wOv到直角坐标平面xOy的一种变换，在此变换下，半径为的圆所围区域D变形为星形线所围区域D′.用平行坐标轴的直线网对区域D′进行分割，任取其中一小块区域△σ′，设其经变换（1）变为区域D的一块小区域△σ，可以证明在不计高阶无穷小的情况下，两块小区域的面积呈如下关系（详细证明参考［9］）：

解 作旋转变换（2），则xOy坐标系下的区域D顺时针旋转45°即是uOv坐标系下的区域D′，如图2所示.

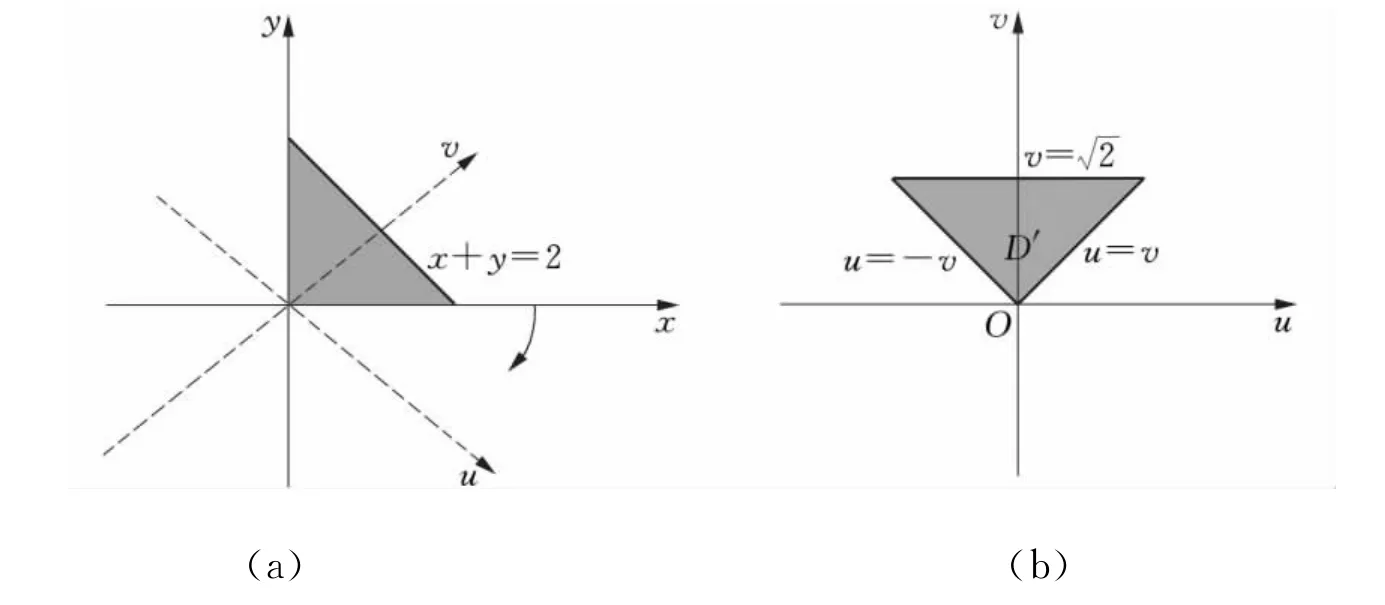
图2

因为旋转变换下，积分区域的形状、大小未发生变化，以区域为底面的曲顶柱体的体积不变，因此

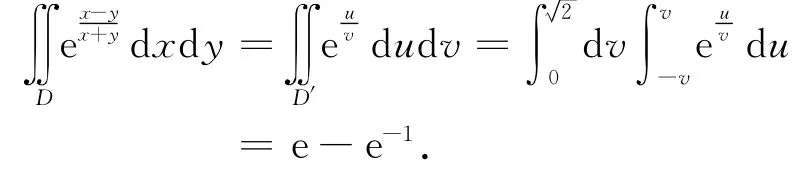
不变量思想对20世纪的整个数学乃至物理学的发展产生了广泛而深刻的影响.从某种意义上说，现代数学就是研究各种不变量的科学［10］.高等数学中很多内容蕴含“不变量思想”，在教学中适时引入它，无疑有益于开阔学生眼界，增进对现代经典数学思想的了解和应用.

［1］路莎·彼得.无穷的玩艺：数学的探索与旅游［M］.朱梧槚译.南京：南京大学出版社，1985.

［2］郭慧莹，张国志.数学思想在高等数学教学中的实证研究［J］.边疆经济与文化，2006，32（8）：127－129.

［3］马秀梅，林距华.高等数学教学中数学思想方法教学途径的探讨［J］.廊坊师范学院学报，2005，21（4）：73－75.

［4］宋卫信，赵有益，张锋.高等数学教学中渗透数学思想方法的探索［J］.当代教育论坛，2011，25（2）：91－93.

［5］同济大学数学系.高等数学（上册）［M］.北京：高等教育出版社，2007：316.

［6］同济大学数学系.高等数学（下册）［M］.北京：高等教育出版社，2007：111－114.

［7］节存来.求旋转体体积的一种新方法［J］.河北农业大学学报，2004，27（5）：117－119.

［8］同济大学数学系.高等数学（上册）［M］.北京：高等教育出版社，2007：280.

［9］同济大学数学系.高等数学（下册）［M］.北京：高等教育出版社，2007：91－93.

［10］李跃武，赵云.代数不变量理论历史演变［J］.西北大学学报（自然科学版），2009，39（1）：160－164.

［11］邵光华.作为教育任务的数学思想与方法［M］.上海：上海教育出版社，2009.

［12］邓明立，张红梅.群论统一几何学的历史根源［J］.自然辨证法通讯，2008，30（1）：75－80.