病态线性方程组新的Jacobi迭代解法

孔祥强

（菏泽学院 数学系，山东菏泽 274000）

Jacobi迭代法是解线性方程组的一种有效方法，它具有存储量小、程序简单的特点.但当方程组的系数矩阵为病态时，该方法不再适用.本文给出了一类全新的Jacobi迭代算法，从而改进和推广了一些已有的结果.

1 Jacobi迭代法

2 新的Jacobi迭代法及收敛性证明

设Ax＝b，其中A非奇异且病态.令A＝D＋M，则Dx＋Mx＝b，在两边同时加上ωFx，ω＞0，变为

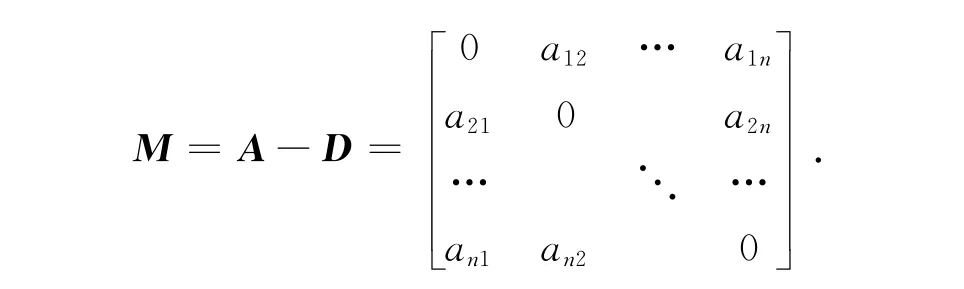
下面研究该迭代法的收敛性.

定义［2］设A∈Rn×n.若存在正对角矩阵D，使AD为严格对角占优矩阵，则称A为广义严格对角占优矩阵.

为了判定一个矩阵是否为广义严格对角占优矩阵，可通过文［3］中的方法，如矩阵

3 数值算例

表1 初值x（0）=（000）T ，迭代9步结果

表2 初值x（0）=（0000）T ，迭代23步结果

若采用文［7］的方法，迭代的次数远超过23次.从表1和表2看出，ω取不同的值时，式（4）的收敛速度不同.相同迭代步数下的误差相差明显.

表3 初值x（0）=（0000）T ，迭代10611步结果

若采用文［6］和［7］的方法，迭代的次数远远超过10611次，因此本文给出的新的Jacobi迭代法对于系数矩阵是Hilbert矩阵的时候也成立.

4 结束语

本文给出了一种求病态线性方程组解的高效迭代算法，该方法具有以下优点：

（i）计算效率高，一般只需迭代数次，即可求得满足精度的近似解.

（ii）迭代公式中ω的选取具有灵活性，当选取的ω适当时，会使计算简便.

（iii）本文方法的收敛速度，不受矩阵阶数的限制.

［1］关治，陈景良.数值计算方法［M］.北京：清华大学出版社，2000，9.

［2］程公鹏.矩阵论［M］.西安：西北工业大学出版社，1999.

［3］徐映红，刘建州.广义严格对角占优矩阵的一组判定条件［J］.工程数学学报，2005，22（4）：733－736.

［4］林胜良.病态线性方程组解法研究［D］.杭州：浙江大学，2005.

［5］易大义，陈道琦.数值分析引论［M］.杭州：浙江大学出版社，2001：305－408.

［6］张艳英，张苹苹，等.病态方程组的一种精确解法［J］.哈尔滨工业大学学报，1995，27（6）：26－28.

［7］富明慧，张文志.病态代数方程的精细积分解法［J］.计算力学学报，2011，28（4）：530－534.