具有阶段结构且发生率为双线性的SIR传染病模型

张慧敏

(中北大学 理学院， 山西 太原 030051)

0 引言

在以往研究的大部分传染病模型[1-6]中，种群无论其年龄大小都假设对疾病有相同的传染力、免疫力、恢复力，然而在现实生活中，由于活动范围与传播途径等因素的影响，许多传染病例如白喉等一般只在成年个体中传播，而幼年个体不易被感染，因此建立具有阶段结构的传染病模型具有较强的现实意义，该方面研究也有了丰硕的结果[7-9].

本文建立了具有两个阶段且发生率为双线性的SIR传染病模型.为了方便讨论，假设只有成年个体感染此病，而幼年种群个体X不感染，且将成年个体分为易感者S，染病者I和恢复者R三部分，只考虑成年易感者具有生育能力，成年染病者会因病死亡，但恢复后可获得终生免疫能力，且假设种群的成熟期比此种传染病平均染病周期要长，设出生率为α,幼年个体夭折比率为γ,β为传染率,d1、d2为死亡率，τ为成熟期，其数学模型为：

初始条件为：

(2)

1 解的非负性和有界性

定理1 当t>0时,系统(1)满足初值X(t)>0,S(t)>0,I(0)>0,R(0)>0,t∈[-τ,0]的解是正的.

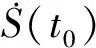
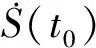
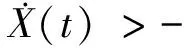
作比较方程

(3)

因方程(3)的解可以表示为

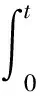
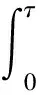
=0.

由(3)可知u(t)是严格减的，所以在t∈(0,τ]，有u(t)>u(τ)=0.由比较定理知，当0≤t≤τ时，有X(t)>u(t)>0.类似文献[10]的方法，可以证明，当nτ0.故当t>0时，X(t)>0.

由系统(1)的第三个方程、第四个方程知

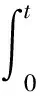
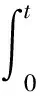
定理2 满足初始条件(2)的系统(1)的正解是最终有界的.

证明：由前面的讨论可知只需考虑

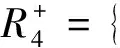
由系统(1)第二个方程知

由比较定理及推论,存在T及ε>0，当t>T时，

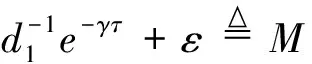
作V(t)=X(t)+S(t)+I(t)+R(t),

V(t)沿系统(1)求导数得

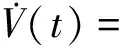
≤αS(t)-γX(t)-d2I(t)-d1R(t)

≤αS(t)-μX(t)-μS(t)+μS(t)-μI(t)-μR(t)

≤(α+μ)S(t)-μV

(4)

其中，μ=min{γ,d1,d2}.

由(4)可得当t>T时，

t→+∞

又因为X(t)>0,S(t)>0,I(t)>0,R(t)>0,

故X,S,I,R最终有界，定理证毕.

2 系统平衡点的稳定性分析

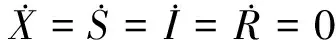
(5)

由此方程组可知系统存在两个边界平衡点

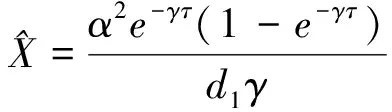
当αβe-γτ>d1(d2+k)时，存在唯一正平衡点E2(X*,S*,I*,R*)，

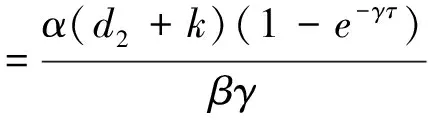
易知E0是不稳定的，下面分析E1、E2的稳定性.

2.1 系统边界平衡点E1的稳定性分析

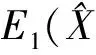
J(E1)=

特征方程为

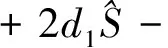
|J(E1)|=(λ+γ)[λ-αe-γτ(e-λτ-2)].

即

(6)

显然λ=-γ,λ=-d1是负根，且λ=αe-γ τ(e-λτ-2)的根均具有负实部，否则

Reλ=αe-γτ[e-γ Reλcos(τlmλ)-2]<0

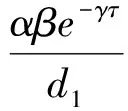
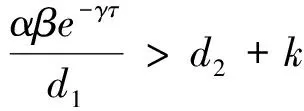
2.2 系统正平衡点的稳定性分析

作代换X0=X-X*,S0=S-S*,I0=I-I*,R0=R-R*仍用X,S,I,R记X0,S0,I0,R0，得系统(1)在E2处的Jacobian特征矩阵为

J(E2)=

特征方程为

|J(E2)|= (λ+γ)[(λ+2d1S*+βI*-αe-(λ+γ)τ)]

·(λ-βS*+d2+k)(λ+d1)+β2S*I*(λ+d1)=0

即

|J(E2)|=(λ+γ)(λ+d1)[λ2+(2d1S*+β(I*-S*)+d2+k)λ

-αe-γτe-λτλ+βI*(d2+k)

+(2d1S*-αe-(λ+γ)τ)(-βS*+d2+k)]

(7)

显然λ=-γ,λ=-d1是负根，对于方程

λ2+(2d1S*+β(I*-S*)+d2+k)λ

-αe-γτe-λ τλ+βI*(d2+k)

+(2d1S*-αe-(λ+γ)τ)(-βS*+d2+k)=0

(8)

因为(2d1S*-αe-(λ+γ)τ)(-βS*+d2+k)=0,

记m=2d1S*+β(I*-S*)+d2+k

n=-αe-γτ<0

p=βI*(d2+k)

则(8)可简化为

λ2+mλ+ne-λ τ+p=0

(9)

记λ=iw,w>0是(9)的一个纯虚根，代入(9)分离实部与虚部得

p-w2+nwsin(wτ)=0,

mw+nwcos(wτ)=0,

消去sin(wτ)及cos(wτ)得关于w的方程

w4+(m2-n2-2p)w2+p2=0

(10)

其根的判别式

Δ=(m2-n2-2p)2-4p2=(n2-m2)(n2+4p-m2)

由(8)知n2-m2<0，所以当n2+4p-m2>0时Δ<0，方程(10)无实根；当n2+4p-m2≤0时，Δ≥0，此时有n2+2p-m2<0，于是有

矛盾，故方程(10)无实根.

当τ=0时,方程(9)变为λ2+(m-α)λ+p=0，当m-α<0时，方程有正根，线性系统的零解不稳定；当m-α>0时，方程的根均具有负实部，线性系统的零解渐近稳定，而方程(10)无根，由文献[11]中的定理3.3.1知，对所有的τ≥0，线性系统在E2(x*,S*,I*,R*) 处的零解是渐近稳定的.因此系统(1)的正平衡点E2局部渐近稳定.

3 传染病灭绝

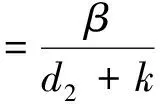
证明：由前面的分析已知系统(1)不存在正平衡点,因此只证边界平衡点E1是全局渐近稳定的.由系统(1)第二个方程知

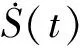
由比较定理及推论知存在T，ε>0，当t>T时，

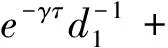
下面，我们证明

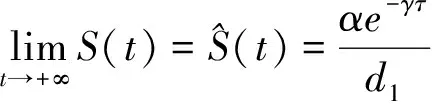
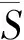
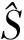
记

(11)

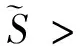
(12)

由系统(1)第二个方程知，在tk处有

(13)

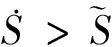
用类似的方法可证

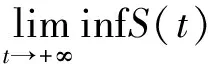
故有

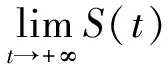
由系统第一个方程知存在T，当t>T>τ时，

X(t)=X(T)e-γ(t-T)

=KS＾〗-e-γτ〗 limt→+∞>∫tTαe-γ(t-y)dy=α

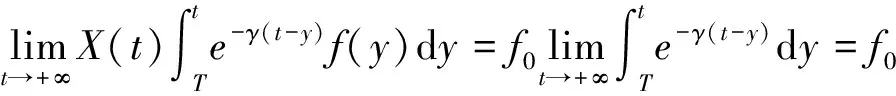
故有

故E1是全局渐近稳定的，也就是说传染病将最终灭绝.

[1] E.Beretta,Y.Takeuchi.Convergence results in SIR epidemic model with varying population sizes[J].Nonlinear Anal.,1997,28(12)：1 909-1 921.

[2] A.Korobeinikov. Lyapunov functions and global stability for SIR and SIRS epidemiological models with non-linear transmission[J].Bull. Math. Biol.,2006,68(3)：615-626.

[3] 马知恩.种群生态学的数学建模与研究[M].合肥：安徽教育出版社，1996.

[4] 陈兰荪,宋新宇,陆征一.数学生态学模型与研究方法[M].成都：四川科技出版社，2003.

[5] Miklos Farkas.Dynamical Models in Biology[M].Academic Press，2001.

[6] Wang Wendi，Chen Lansun. A Predator-prey System with Stage-structure for Predator[J].Computers & Mathematics with Applications，1997,33(8)：83-91.

[7] 原存德,胡宝安.具有阶段结构的SI传染病模型[J].应用数学学报，2002，25(2)：194-203.

[8] 胡宝安,陈博文,原存德.具有阶段结构的SIS传染病模型[J].生物数学学报，2005，20(1)：58-64.

[9] 郑丽丽，柳合龙.按时滞转化的阶段结构SIS传染病模型[J].数学的实践与认识，2005，35(7)：159-166.

[10] J.D.Murray.Mathematical biology[M].Springer，1993.

[11] Yang Kuang.Delay differential equation with application in population dynamics[M].Academic Press,Inc,1993：76-77.