一类带PML光波导中的共轭特征算子构造

郭 琼，朱燕芝，马云娟

（杭州师范大学理学院，浙江 杭州 310036）

一类带PML光波导中的共轭特征算子构造

郭 琼，朱燕芝，马云娟

（杭州师范大学理学院，浙江 杭州 310036）

将无界三层带有不平坦界面的光波导经坐标变换和完美匹配层截断近似转化为有界且带有平坦界面的光波导，利用复Helmhotz方程求解波的传播计算问题，推导出了该复偏微分方程的共轭特征函数所满足的方程，并论证了方程的特征函数与共轭特征函数正交之性质，同时给出局部基下坐标计算的简便公式.

完美匹配层；共轭特征函数；Helmholtz方程；局部坐标变换；横电波导

光波导在介质中的传播，在数学上归结为著名的Helmholtz方程.当传播区域或求解范围有界时，Helmholtz方程的特征函数具有加权正交的性质，因此可以采用步进算法快速求解Helmholtz方程，并已取得了很好的数值解.然而，当考虑传播区域或求解范围无界时，如无限深的海洋、上下无界的光传播域，通常的数值方法对此类问题的处理严重失效.

曾有人构造了精确的边界条件，将无界区域问题化为有界问题区域问题，但此条件涉及到广义积分，导致数值计算上的困难.值得庆幸的是1994年引进了完美匹配层，将无界求解区域截断、近似转化为一个有界的区域[1－4]，而实的Helmholtz方程转化为一个复偏微分方程，这在数学上相当于对Helmholtz方程作了一个复伸展变换.针对上述复偏微分方程，关于平坦界而的情形已推导出了与该方程的特征函数系正交的共轭特征函数系所满足的方程[5－8]，并给出了特征函数系及其共轭特征函数系的解析表达式，实现了不同局部基下的坐标转换和方程变换的快速计算[9－10].

本文进一步将研究推广到弯曲界面情形，研究三层带弯曲界面的无界光波导中共轭特征算子构造，争取得到更一般的结果.

1 特征方程及其性质

光波导的波动方程通常可以简化为Helmholtz方程：

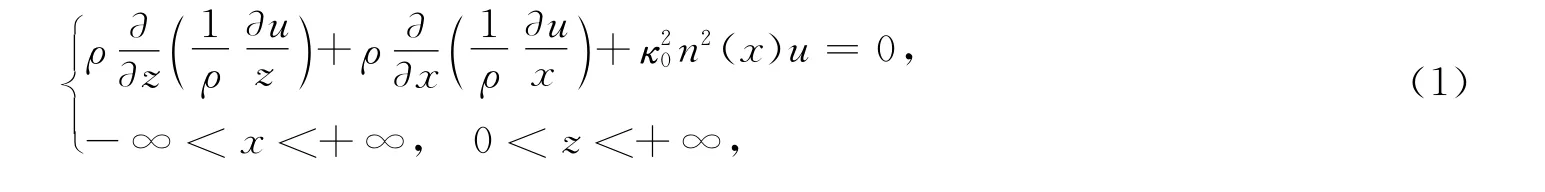
其中

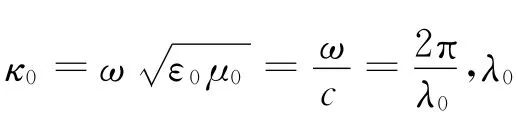
设折射率n（x）为分段函数：

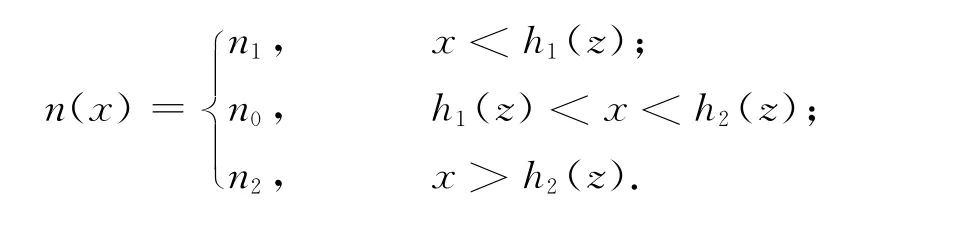
TE情形下方程可简化为：

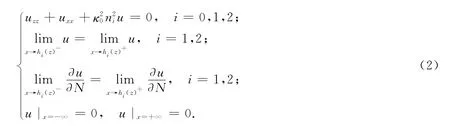
其中：h1（z），h2（z）是弯曲的内界面，N表示界面的法向量.由于现有的步进算法不适合弯曲界面情形，故首先需引入正交变换：＝g（z，x）＝f（z，x）.

式（2）定义在无界区域中，在这样的前提下，如果采用数值计算，则离散的区域是无限的.此时需要增加一定的条件才能将无界的区域转化为有界的区域来求解，因此可引入完美匹配层做为吸收介质，使得当波由区域内通过界面传到完美匹配层时，一般不会发生反射.PML的引入，相当于作了一个复伸展坐标

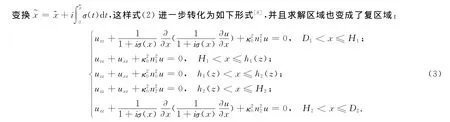
本文需要解决的问题中有两个弯曲界面，这种弯曲的界面有两种处理方式.一种是采用折线法近似代替原先的弯曲界面，这样在每一个水平防线的小区间中，弯曲界面将被近似看成直线界面，因此就可以将原来整个弯曲界面求解问题转化为一系列平坦小区间上的求解问题.此方法易实现，但同时也带来了一对矛盾，当划分不是非常小的时候，误差将会很大，而如果想加密分点则会让问题的计算量变得非常大.另一种方法就是通过坐标变换，将带有弯曲界面的区域变换成平坦的界面.典型的坐标变换法有3种：全局变换、局部非正交变换和局部正交变换.经过比较发现，采用局部正交变换可以使界面条件变得相对容易一些，同时新旧坐标之间可以通过牛顿迭代来实现.

下面讨论局部正交变换.

（i）在下包层即 H1≤x≤h1（z）区域内，取局部坐标变换[6]：

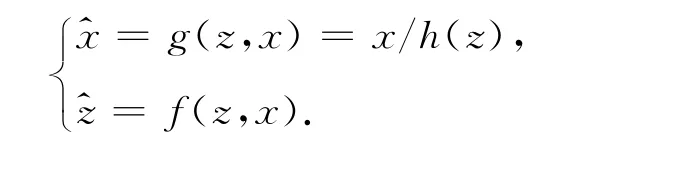
2 特征问题

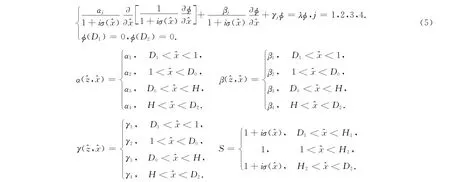
其中αi，βi，γi，i＝1，2，3，4，见附录.

其界面条件为

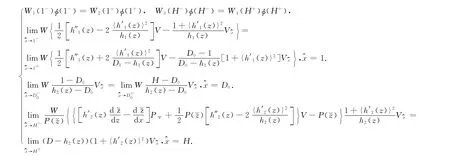
3 共轭特征算子的构造

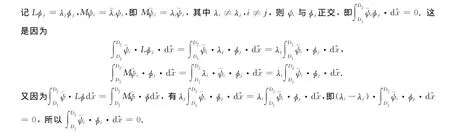
4 结 论

从Helmholtz方程出发，引入局部正交部变换和方程变换，将Helmholtz方程0转化为，从而实现弯曲界面的平坦化.再引入PML将无界区域上的波传播问题转化为有界区域上的波传播问题.并构造了算子L的共扼算子M，论证了算子L的特征函数与共轭算子M的特征函数具有正交性质.此方法在传播计算中的更深入应用有待进一步开发.

[1]Lassas M，Helsinki E S.On the existence and convergence of the solution of PML equations[J].Computing，1998，60（3）：229-241.

[2]Turkel E，Yefet A.Absorbing PML boundary layers for wave-like equations[J].Appl Numer Math，1998，27（4）：533-557.

[3]Berenger J P.A perfectly matched layer for the absorption of electromagnetic waves[J].J Comp Physics，1994，114（2）：185-200.

[4]Rogier H，Zutter D.Berenger and leaky modes in microstrip substrates terminated by aperfectly matched layer[J].IEEE Transactions on Microwave Theory and Techniques，2001，49（4）：712-715.

[5]Lu Yayan，Zhu Jianxin.A local orthogonal transform for acoustic waveguides with an internal interface[J].J Computational Acoustics，2004，12（1）：37-53.

[6]Lu Yayan，Huang Jinyang，Mclaughlin J R.Local orthogonal transformation and one-way methods for acoustics waveguides[J].Wave Motion，2001，34（2）：193-207.

[7]Zhu Jianxin.Local orthogonal transformation for acoustic waveguide[J].Appl Math J Chinese Univ，2000，15（4）：443-452.

[8]Zhu Jianxin，Li Peng.Local orthogonal transform for a class of acoustic waveguide[J].Progess in Natural Science，2007，17：18-28.

[9]Zhu Jianxin，Lu Yayan.Leaky modes of slab waveguides-asymptotic solutions[J].Journal of Lightwave Technology，2006，24（3）：1619-1623.

[10]朱建新，钱微微.一类带PML声波导中的共轭特征函数构造及其应用[J].浙江大学学报：理学版，2007，34（6）：605-608.

附 录

Construction of Conjugate Characteristic Operator for a Class of the Optical Waveguides with PML

GUO Qiong，ZHU Yan-zhi，MA Yun-juan
（College of Science，Hangzhou Normal University，Hangzhou 310036，China）

The unbounded optical waveguide with three curved interfaces were converted into the bounded optical waveguide with flat interfaces by coordinate transform and terminated by the perfectly matched layer.The paper used the improved and complex Helmholtz equation to solve the wave propagation problem，deduced the equation for the conjugate eigenfunctions of improved and complex Helmholtz equation，proved the orthogonal property between the characteristic eigenfunctions and the conjugate eigenfunctions，and provided a simple formula for calculating the coordinates under the local bases.

perfectly matched layer；conjugate eigenfunction；Helmholtz equation；local coordinate transform；TE

O174.41 MSC2010：47H10；54H25

A

1674-232X（2012）04-0323-08

11.3969／j.issn.1674-232X.2012.04.008

2011-12-02

朱燕芝（1987—），女，应用数学专业硕士研究生，主要从事科学计算研究.E-mail：lengyue1111＠163.com