固体推进剂/衬层界面裂纹的界面层模型有限元分析①
邸 克,杨月诚,张昆鹏
(第二炮兵工程大学601室,西安 710025)
0 引言
固体火箭发动机推进剂/衬层界面裂纹问题是影响固体发动机工作可靠性的关键因素。因此,该类问题一直受到学者们的广泛关注。人们主要采用实验和以有限元为主的数值方法对其研究。在实验方面,阳建红等[1]采用X射线观测了推进剂的脱粘扩展试件燃烧过程。在有限元法方面,王至存等[2]对推进剂/衬层/绝热层矩形粘结试件进行了三维粘弹性应力分析,蒙上阳等[3]计算了推进剂/衬层中不同深度脱粘裂纹的应力强度因子。但该类界面粘结区域的细观结构或模量对裂纹的影响研究尚未见报道,其根本原因是缺乏一个合适的推进剂/衬层界面力学模型。
为有效地研究界面力学问题,人们提出了多种界面模型,如理想界面模型[4]、粘着层界面模型[5]和接触界面模型[6]等。而对真实情况下的NEPE推进剂/衬层界面,吴丰军等[7]应用纳米压痕仪证实了它是模量和硬度呈现梯度变化的结构,这为功能梯度界面层模型在推进剂/衬层界面裂纹中的应用提供了实验基础。功能梯度界面层模型[8]是将双材料界面粘结区域视为功能梯度材料(FGM),并充分考虑了细观层面的界面粘结结构对整个模型的影响。早期,该模型一般采用某一种函数[9]表示界面层材料属性的变化。而在最近几年,人们将界面层划分成两层[10]或多层[11]。其中,每一层内分别采用了不同的函数描述材料属性分布。
在多数情况下,人们对于功能梯度界面层模型的研究采用理论推导方法,通过求解奇异积分方程获得裂纹的应力强度因子。但这种理论研究难以获取模型应力应变的分布规律。另外,在理论研究时,为了能推导出控制方程的解析解,模型中许多参数的设定均受到一定限制,这使得该模型在工程应用方面还有一些欠缺。为此,本文将功能梯度界面层模型和有限元方法结合,为固体推进剂/衬层界面建立了一个新的界面层模型,应用软件ABAQUS及其二次开发程序,获取了推进剂/衬层界面裂纹尖端附近的应力应变场,以及Ⅰ和Ⅱ型粘弹性应力强度因子随加载时间的变化规律。
1 界面层模型和参数
文献[7]中说明,衬层和推进剂粘结在一起时,由于材料的相互扩散和渗透,粘接处形成了模量快速上升区和模量快速下降区,这两个模量变化区域组成界面层区。因此,本文中界面层的厚度即可看成上述两个模量变化区域的总厚度。对于真实的推进剂/衬层粘接试件,界面层相对于衬层和推进剂厚度很小,而界面层模量分布又较复杂。为了突出研究重点以及节约计算量,本文根据文献[7]中的数据,作适当简化后,建立了推进剂/衬层界面的二维平面应力模型。其中,各层均为粘弹性材料(示意图和有关参数的取值分别如图1和表1所示)。

在界面层左侧的中线处设置一长度为c的裂纹,界面层两侧的衬层和推进剂初始弹性模量分别是E1和E3,且它们不随厚度的变化而变化。模型将界面层划分成上中下3个区域,设界面层中间区域材料的初始模量为Er(和厚度无关),通过变化Er体现界面层整体模量的变化。此外,界面层内上下两个区域中,材料初始弹性模量随厚度线性变化。计算时,选取界面层上中下3个区域厚度比为3∶2∶3,并假设模型各层材料松弛模量均写成初始模量和时间因子相乘的形式[12]:

为了保证各层材料界面处松弛模量的连续性,假设各层材料时间因子f(t)相同,这里将f(t)写成Prony级数形式:


表1 模型中各参数的取值Table 1 Values of the parameters in the model
2 有限元模型和计算工况
对模型进行有限元网格划分时,各处均采用八节点四边形平面应力单元(CPS8),并在裂纹尖端附近加密网格,其整体和局部网格分别如图2和图3所示,模型共划分为9 854个单元。

裂纹尖端处网格划分成环状结构,以便于采用围线积分技术计算应力强度因子。计算时,各层材料的粘弹性本构方程均可写成以下积分形式:
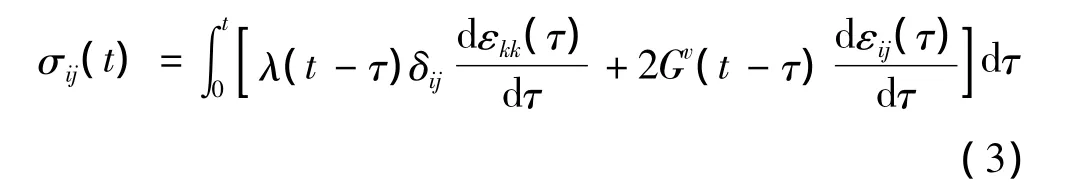
其中,λ为拉梅常数,Gv为剪切松弛模量,它和弹性松弛模量Ev的关系为为泊松比)。对于该模型的平面应力问题,部分应力应变分量均为0,应力 σij中只须考虑分量 σxx、σxy和 σyy;应变 εij中只需考虑分量 εxx、εyy、εzz以及 γxy。
采用子程序USDFLD定义空间场变量,以实现材料初始模量随界面层厚度的梯度变化。本文根据功能梯度材料属性变化,将y坐标定义成场变量,并设置材料的初始弹性模量是y坐标的函数。这时,界面层中各部分初始弹性模量分别表示为
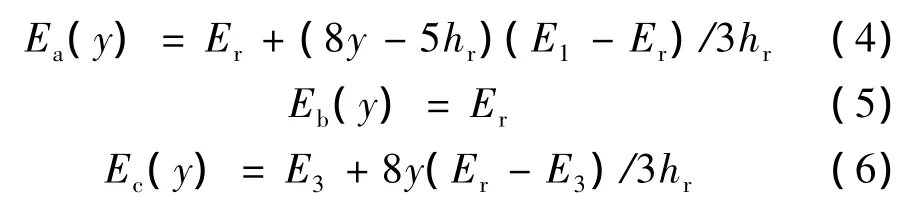
以上3式中,Ea、Eb和Ec分别表示界面层内上中下3部分。将它们写入子程序USDFLD,即可有效地表征功能梯度界面层的模量变化。
考虑法向和剪切两类加载条件,并在裂纹上下两端面施加位移载荷。两类加载条件下,均约束图1中B和D两顶点全部自由度,而且位移载荷均在1 s内由0线性增加到额定值0.001 mm,随后保持99 s。
3 计算结果与分析
根据文献[7]的实验结果,当推进剂/衬层界面贮存时间延长时,界面层弹性模量明显减小。计算时,令Er取3、18、40 MPa 3个特殊值,以体现不同界面层模量对结果的影响规律。这3个值也可分别看成是界面贮存后期、中期和前期的界面层模量。计算结果中,默认采用Von Mises等效应力(MPa)和最大主应变分别描述最终时刻的应力和应变场。
3.1 不同精细度模型结果比较
为了证明计算的有效性,本文将不同精细度模型的计算结果进行比较。以图2的网格结构为基准,重新划分了疏密两个网格模型,其单元个数分别为7 162和13 484。在法向位移加载条件下(Er=18 MPa),计算了裂纹尖端节点法向应力随时间的变化,结果如图4所示。从图4可看出,随着模型精细度的提高,各时刻应力逐渐趋向于某一定值。这说明图2构建的模型精细度符合计算要求,网格划分到此程度已经收敛。
3.2 应力应变场
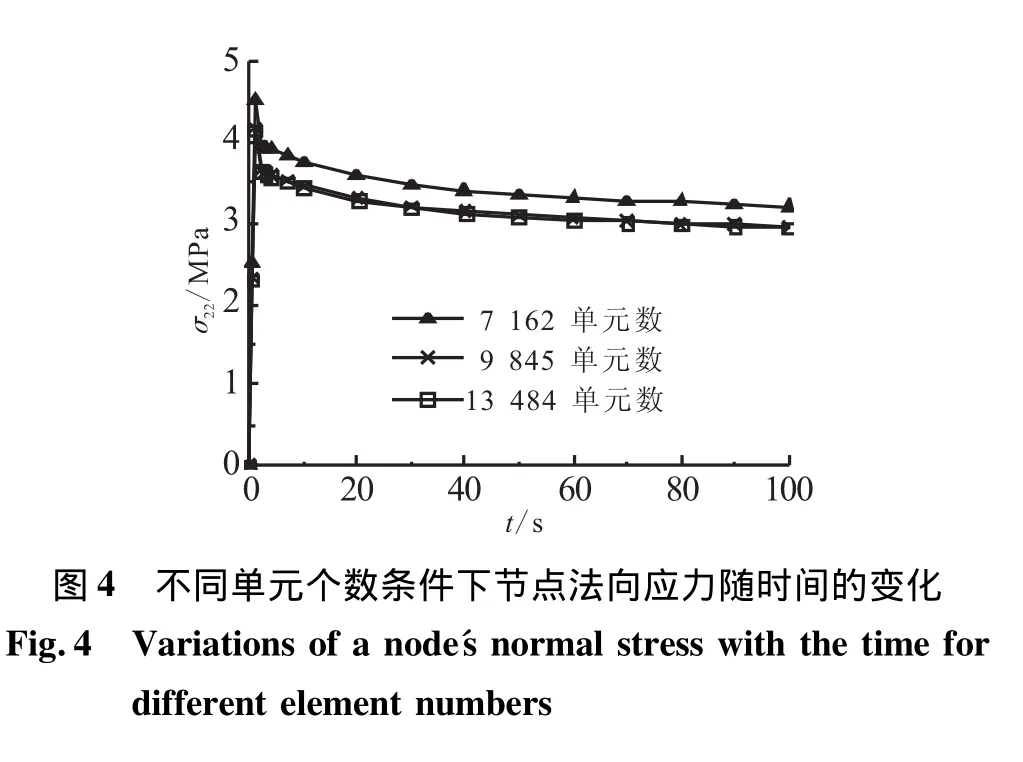
图5和图6分别显示的是法向和剪切位移加载下的应力场。可看出,当界面层模量增大时,裂纹尖端附近应力整体分布及最大值明显增大。在界面贮存前期,由于界面层模量明显高于两侧推进剂和衬层的模量,在界面层处产生了一个应力相对较大的带状分布。在界面贮存后期,法向和剪切位移加载下应力最大值分别为贮存前期的8.01%和7.84%。因此,可得结论:随贮存时间延长,裂纹尖端附近应力场明显减弱。
法向和剪切位移加载下,不同界面层模量条件下的应变场如图7和图8所示。这时,随着界面层模量增大,裂纹尖端附近应变最大值略有减小。在界面贮存前期,界面层处存在一个应变相对较小的带状分布,到界面贮存后期,这种带状分布基本消失。以上说明,随着贮存时间的延长,裂纹尖端附近的应变最大值略有增大,而界面层处应变也逐渐变大。

3.3 应力强度因子
法向位移加载下Ⅰ型和剪切位移加载下Ⅱ型应力强度因子(KⅠ和KⅡ)随加载时间的变化规律分别如图9和图10所示。
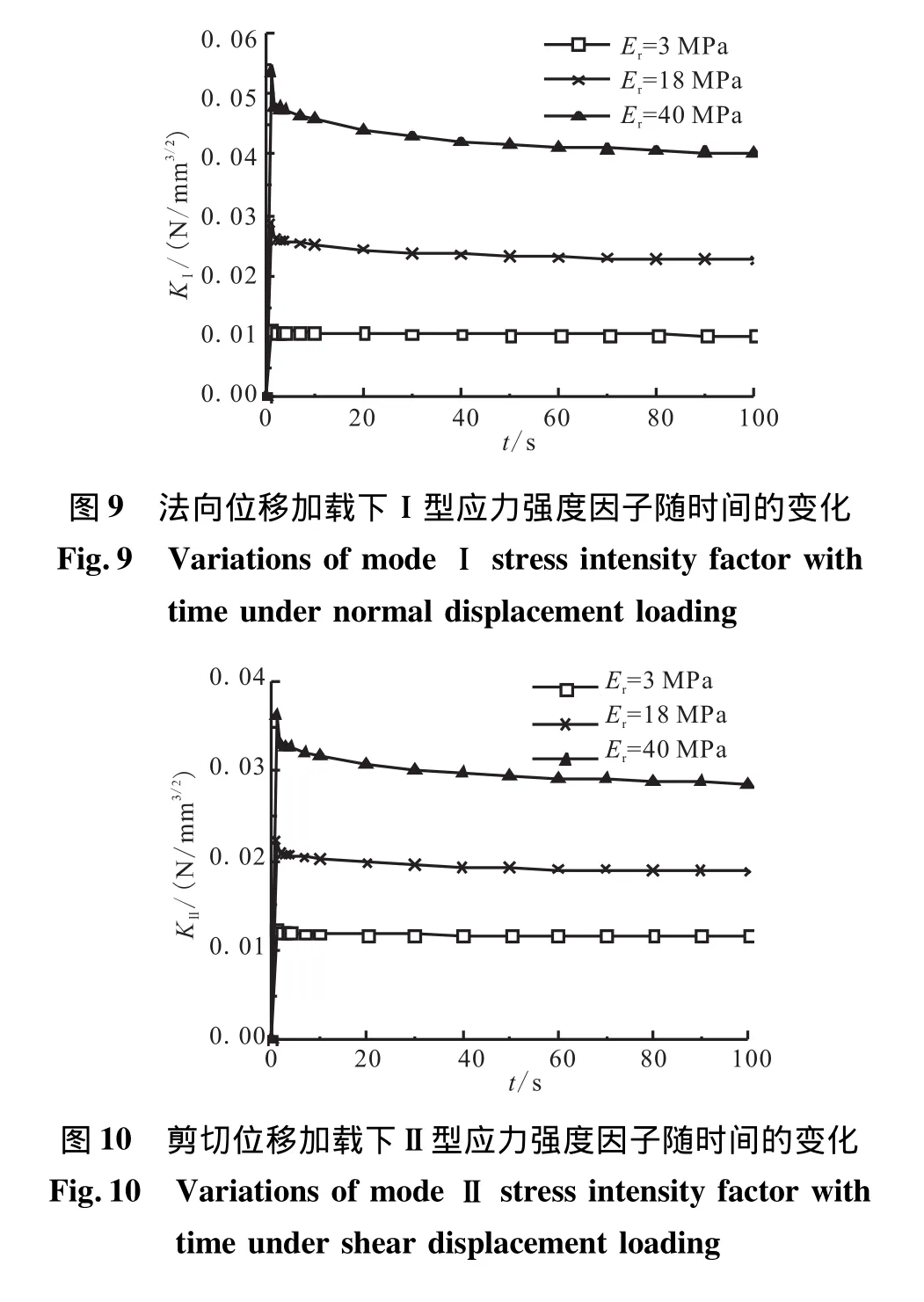
KⅠ和KⅡ的变化规律相似,均随界面层模量的增大而增大,这表明裂纹处材料的相对刚度越大,Ⅰ和Ⅱ型应力强度因子越大。对于此变化规律,本文的数值计算和相应的理论分析[13]是一致的。此外,在位移载荷刚好增加到额定值时(t=1s),KⅠ和KⅡ均达到最大值,随后缓慢下降,体现出粘弹性材料的应力松弛特征。其中,界面层模量越大,这种下降趋势越明显。由上述分析可知,法向位移加载下的KⅠ和剪切位移加载下的KⅡ均随着界面贮存时间的延长明显减小。
综上计算结果可看出,界面层模量随界面贮存时间的延长而减小时,裂纹尖端附近的应力应变场以及裂纹应力强度因子均产生一定的变化。因此,在求解推进剂/衬层界面裂纹问题时,应充分考虑界面层模量(或界面贮存时间)对其影响,这也同时说明本文模型的建立是十分必要的。
4 结论
(1)在实验的基础上,建立了一个固体推进剂/衬层界面裂纹的界面层有限元模型。相对于其他界面力学模型,该模型可充分考虑到界面层模量的分布及变化趋势,进而揭示推进剂/衬层界面贮存时间对断裂参量的影响规律。相对于功能梯度界面层的理论模型,该模型可更方便地获得应力和应变的分布规律。
(2)计算结果表明,随着界面贮存时间的延长,裂纹尖端附近应变的最大值略有增大,而整体应力和应力强度因子明显减小。其中,在界面贮存后期,法向和剪切位移加载下应力最大值分别减小到贮存前期的8.01%和 7.84%。
(3)本文工作对功能梯度界面层模型和数值方法的结合,以及该模型在工程方面的应用有一定的借鉴意义。另外,本文也为精确分析推进剂/衬层界面裂纹问题提供了有效的参考。在此后的工作中,该模型可扩展至三维情况,用来分析固体发动机推进剂/衬层界面裂纹问题。
[1]阳建红,侯根良,刘朝丰,等.燃烧条件下药柱脱粘扩展的设计[J].推进技术,2004,25(3):274-277.
[2]王至存,朱祖念,张善祁.固体发动机药柱粘结试件的三维应力分析[J].宇航学报,1996,17(4):34-38.
[3]蒙上阳,唐国金,雷勇军.固体发动机包覆层与推进剂界面脱粘裂纹稳定性分析[J].固体火箭技术,2004,27(1):46-49.
[4]Williams M L.The stresses around a fault or crack in dissimilar media[J].Bulletin of the Seismological Society of America.1959,49(2):199-204.
[5]Atkinson C.On stress singularities and interfaces in linear elastic fracture mechanics[J].International Journal of Fracture,1977,13(6):807-820.
[6]Comninou M.The interface crack[J].Journal of Applied Mechanics,1977,44(4):631-636.
[7]吴丰军,彭松,池旭辉.NEPE推进剂/衬层粘接界面层厚度表征方法研究[J].固体火箭技术,2008,31(6):650-652.
[8]Delale F,Erdogan F.On the mechanical modeling of the interfacial region in bonded half-planes[J].Journal of Applied Mechanics,1988,55(2):317-324.
[9]Ozturk M,Erdogan F.Antiplane shear crack problem in bonded materials with a graded interfacial zone[J].International Journal of Engineering Science,1993,31(12):1641-1657.
[10]Li Y D,Lee K Y.Mechanical modeling and transient antiplane fracture analysis for the graded inter-diffusion regions in a bonded structure[J].Meccanica,2009,44:389-408.
[11]Huang G Y,Wang Y S,Yu S W.Fracture analysis of a functionally graded interfacial zone under plane deformation[J].International Journal of Solids and Structures,2004,41:731-743.
[12]Jin Z H.Some notes on the linear viscoelasticity of functionally graded materials[J].Mathematics and Mechanics of Solids,2006,11(11):216-224.
[13]Cheng Z Q,Gao D Y,Zhong Z.Interface crack of two dissimilar bonded functionally graded strips with arbitrary distributed properties under plane deformations[J].International Journal of Mechanical Sciences,2012,54:287-293.

