基于共享铺层融合技术复合材料层压板铺层顺序优化设计①

陈景昊，孙 秦，范学领

(西北工业大学航空学院，西安 710072)

0 引言

纤维增强复合材料因其优异的材料、力学性能和良好的可设计性被广泛用于航空、航天、船舶、汽车等诸多领域。复合材料层压板铺层角度和铺层顺序对层压板弯曲、屈曲和振动等多项特性具有显著的影响，是复合材料结构设计的基础和关键技术之一［1－4］。随着结构承载能力及轻量化要求的不断提高，含丢层结构复合材料越来越广泛用于现代工程结构中，这将导致在复合材料结构铺层设计过程中极易出现刚度丢失现象。因此，如何有效地选择丢层结构铺层优化设计方案，不仅关系到结构是否具有最优的刚度和稳定性，而且对结构重量的最优化有着重要影响［5－7］。

本文在共享铺层融合(Shared Layers Blending，SLB)技术和遗传算法基础上，提出了一种基于层压板面内刚度和弯曲刚度的含丢层复合材料两级优化铺层设计方案，通过实例验证了该方法在含丢层复合材料层压板铺层顺序优化设计中的有效性。

1 复合材料层压板刚度优化设计原理

根据经典层合板理论推导，对于厚度h的N层层压板，其合力N与合力矩M的矩阵表达式为

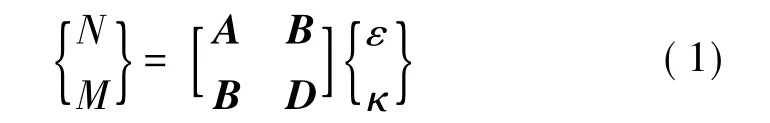
其中，ε为应变;κ为扭曲率;A、B和D分别是抗拉刚度、耦合刚度和弯曲刚度矩阵，矩阵中各元素为

式中 hk=zk－zk－1为第 k层铺层的厚度;zk－1)/2是第k层铺层中面的厚度方向(z向)坐标值，为单层板偏轴刚度矩阵。

以对称均衡复合材料层压板结构为例，其刚度仅与抗拉刚度A和弯曲刚度D相关，具体而言，A11、A22、A66和D11、D22、D66在刚度计算中起决定性因素。因此，在复合材料离散优化方案中，抗拉刚度矩阵A和弯曲刚度矩阵D可用衡量复合材料结构刚度变化。

为此，本文以 A11、A22、A66和 D11、D22、D66为优化参数，以面内刚度A和弯曲刚度矩阵D为优化目标函数，引入权因子pi和qi(i=1，2，3)，进行多目标函数优化设计:

其中

权因子pi和qi的引入，可避免结果在Aii或Dii影响较小的区域收敛。

2 含丢层复合材料层压板优化设计方法

2.1 共享铺层融合法

在实际工程应用时，不同区域复合材料层压板厚度通常随着结构受力特性的变化而改变。以机翼蒙皮为例，机翼承受展向气动载荷，并从翼尖到翼根累加，故机翼蒙皮沿翼尖到翼根、前缘到后缘方向复合材料层压板厚度不断增加。实际工程处理过程中，可在机翼不同部位铺设不同厚度蒙皮，此时可将蒙皮视为由多板结构组成，板与板之间由于铺层厚度的不同，造成结构内铺层丢失，形成丢层结构。丢层结构一旦出现，将可能带来层压板结构刚度丢失以及相邻板块之间出现应力集中问题。为了解决丢层结构带来的工程铺层问题，一种合理的板块间铺层策略-共享铺层方法(SLB方法)近年来被提出，并用于丢层层压板结构优化设计［8－9］。

以图1所示划分为6个区域的复合材料层压板为例，说明共享铺层融合法的基本分析过程。

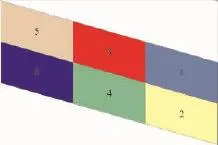
图1 六板共享铺层法Fig.1 Illustration of shared layers blending(SLB)method for six-panel composite laminates

(1)以商业有限元初步优化结果得到6块板的初始铺层角度及其相应厚度(通常单层板厚度相同，因而总厚度与总铺层数是对应的)为例，此处简化起见，假设各板块均仅含0°、±45°和90°铺层，其中1号板15/12/4;2号板16/11/3;3号板17/6/5;4号板14/5/2;5号板15/2/5;6号板13/2/3。

(2)搜索1～6号板块中铺层数最少，也即最薄板，本例中为6号板。统计所有板块中各角度铺层(即0°、±45°和 90°)的最少层数，为 13/2/2，将该铺层数集合作为第一共享铺层单元铺设于结构最外层。

(3)确定各板块剩余铺层(初始铺层去除第一共享铺层所余铺层，如最薄板6号板剩余铺层为0/0/1)。在最薄板(6号板)之外的其余各板(1～5号板)剩余铺层中搜索公共铺层，得到第2共享铺层，本例为1/0/0。此轮搜索最薄板5号板的剩余铺层为1/0/2。

电工培训正是为了促使电工紧跟当前经济、技术发展方向，不断进行新理论、新知识、新技术、新方法为主的知识更新和能力提升。传统电工培训存在教学环境封闭、孤立的弊端，不能结合新技术、新材料、新工艺开展，造成培训内容滞后、与社会发展需要脱节，培训质量不高。笔者通过浅析信息技术对南疆村镇电工培训效果的影响，探讨提升培训质量的方法。

(4)依此类推，自1～4号板搜索得第3共享铺层0/3/0，最薄板4号板剩余铺层为0/0/0;自1～3号板搜索得第4共享铺层1/1/1，最薄板3号板剩余铺层为2/0/2;自1号和2号板中得到第5公共铺层0/5/0，最薄板1号板剩余铺层为0/1/1和2号板剩余铺层为1/0/0。

(5)然后，采用上述方法对各板剩余铺层进行公共铺层分析，5号板与6号板间存在第6共享铺层0/0/1;5号板与3号板间有第7公共铺层1/0/1;3号板与1号板间存在第8共享铺层0/0/1。

(6)依次将各共享铺层自外向内铺设，即得最终层压板优化铺设顺序。

2.2 遗传算法设计

遗传算法(Generic Algorithm，GA)是一种基于自然选择和基因遗传学原理的智能优化搜索算法。采用遗传算法进行离散变量优化，可很好地解决含丢层结构复合材料层板优化目标函数难求导、决策变量实际值难确定等问题，通过概率搜索技术和适应度函数概念，能有效地把搜索范围集中在适应度较高的范围内，提高搜索效率，因而被广泛用于航空、航天结构优化设计中［10－11］。

(1)编码及种群初始化

以仅含0°/±45°/90°复合材料铺层优化设计问题为例，可直接采用数组0、45、90、－45作为个体元素的编码方式，即可将{0/90/45/…/－45/0}直接编码形成一个初始个体，利用数组交换规则对n层区域形成n!个个体的初始种群。

在遗传算法中，对于满足交换条件的父代，采用其自身的单随机点前后位互换方法生成子代个体。例如，当父代个体{0/90/45/…/－45/0}满足交换条件时，若随机点为第2个个体，则个体数组随机点前元素与随机点后元素进行交换，得到子代个体{90/45/…/－45/0/0}。

(3)变异

与交换原理一样，为了保证结果随机性，又不会造成个体层数遗失或增加，故采取一种两随机变异点交换原理，实现子代种群的多样性。仍以个体{0/90/45/…/－45/0}为例，当随机变异点为2位和3位时，进行2、3位元素互换得到新个体{0/45/90/…/－45/0}。由于变异点选取的随机性，能合理地实现在整个搜索范围内的变异。

2.3 含丢层复合材料层压板优化流程

综合连续变量优化到离散变量优化的全过程，结合有限元软件、共享铺层融合法和遗传算法原理，将铺层顺序作为种群个体，以F1、F2为目标函数，最终获得使丢层结构刚度增强的最优铺层顺序方案。图2给出了基于面内刚度和弯曲刚度的丢层结构复合材料层压板整体优化策略。

3 实例

本节以三区域分块复合材料层压板铺层优化为例，验证上述方法的有效性。

根据所计算层压板性质，考虑到对弯曲刚度系数的求解，层压板右端厚度方向上施加垂直于层压板中性面的外载荷。选取复合材料T300/N5208为各个铺层用材料，其材料属性见表1。

选取各板块0°、±45°和90°的铺层厚度为设计变量。由于设计准则要求±45°铺层数相同，因而对所研究三板结构层压板而言，共有9个变量需要进行优化。表2给出了采用Patran/Nastran对3块板进行初级优化所得数值结果。

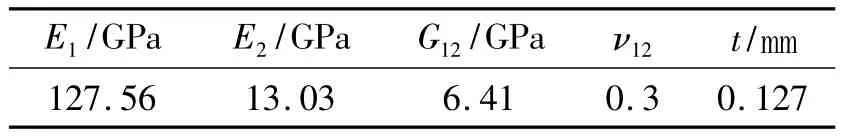
表1 复合材料T300/N5208材料属性Table 1 Material properties of T300/N5208

图2 复合材料层压板优化流程图Fig.2 Optimization procedure of composite laminates

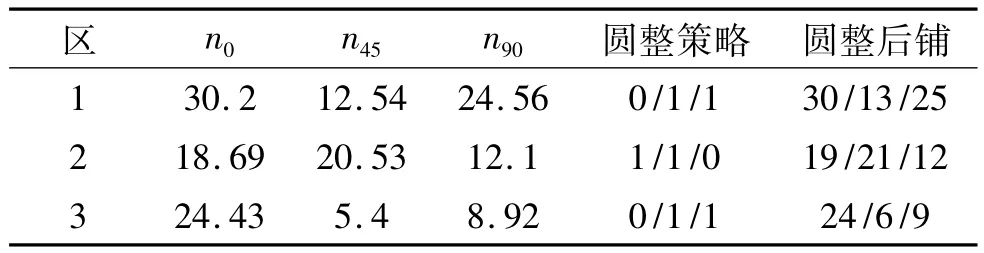
表2 商业有限元初始优化铺层数据及其圆整策略Table 2 Initial ply numbers and related round-off strategy

基于丢层结构对面内刚度的影响，采用向下圆整策略，将会导致每个铺向角不满整数层厚度的损失。结合重量最优原理，可将损失厚度在最多四层内进行优化。因此，基于不减小面内刚度的原则，将损失厚度优化为整数层数，所得圆整策略如表2所示。表2中，最后一列为圆整后铺层，是共享铺层法初始铺层数据。

采用共享铺层融合法各分区进行共享铺层处理，共有两个共享铺层。其中，第1共享铺层为18/5/8，第2共享铺层为0/7/4。3个区域的剩余铺层(n0/n45/n90)分别为12/0/12、0/8/0 和6/0/0。

根据多目标优化思想求解各区域弯曲刚度权因子qi，并对弯曲刚度矩阵对角元素Dii进行优化，结果如表3所示。

在采用遗传算法对层压板参数进行铺层顺序优化时，所选取种群繁殖代数为200代，交换概率为0.6，变异概率为0.1。最后，得到三板分区层合板铺层优化顺序如表4所示。

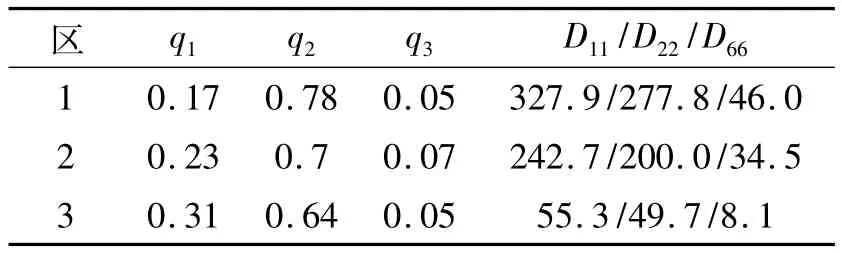
表3 多目标优化权因子及优化后弯曲刚度矩阵系数Table 3 Weighting factors qiand resulted elements of bending stiffness matrix

表4 基于刚度复合材料层压板铺层顺序优化结果Table 4 Optimized ply sequences of the composite laminates

4 结论

针对含丢层复合材料层压板结构在工程应用中的铺层顺序优化问题，提出了一种基于面内刚度和弯曲刚度的复合材料层压板铺层优化方法。该方法集成并发扬了共享铺层融合技术和遗传算法的优点，不仅可有效处理对商业有限元软件初步连续变量优化结果进行圆整所带来的刚度损失问题，而且在离散变量优化过程中，可保证结构的面内刚度大于第一级优化结果。最后，通过实例验证了该方法在复合材料铺层优化设计中的有效性。

［1］章怡宁，杨旭.复合材料翼面结构综合优化设计技术［J］.航空学报，1997，18(6):656-660.

［2］张彦考，张铎.大型复合材料结构优化设计方法研究［J］.固体火箭技术，2003，26(3):69-71.

［3］Wu H，Yan Y，Liu Y J.Reliability based optimization of composite laminates for frequency constraint［J］.Chinese Journal of Aeronautics，2008，21:320-327.

［4］Wu H，Yan Y，Yan W，et al.Adaptive approximationbased optimization of composite advanced grid-stiffened cylinder［J］.Chinese Journal of Aeronautics，2010，23:423-429.

［5］修英姝，崔德刚.非对称非均衡复合材料铺层优化设计［J］.航空学报，2004，25(2):137-139.

［6］彭超义，曾竟成，肖加余，等.整体复合裙的铺层比优化设计与轴压性能分析［J］.固体火箭技术，2006，29(3):208-211.

［7］李太鹏，徐元铭.基于PATRAN/NASTRAN的复合材料结构铺层的分级优化设计方法［J］.固体火箭技术，2004，27(4):308-315.

［8］Liu D Z，Toropov V V，Querin O M，et al.Bilevel optimization of blended composite wing panels［J］.Journal of Aircraft，2011，48:107-118.

［9］Liu D，Toropov V V.Optimization of blended composite wing panels using smeared stiffness technique and lamination parameters［R］.AIAA 2010-3079.

［10］何景轩，田维平，何国强，等.基于遗传算法的固体火箭发动机参数优化设计［J］.固体火箭技术，2004，27(4):250-254.

［11］孙丕忠，张育林.正交设计遗传算法在固体火箭优化设计中的应用［J］.固体火箭技术，2003，26(1):19-26.