基于HyperWorks的折叠翼结构优化设计①

王晓慧，郑海峰，刘昊鹏，赵国伟

(1.北京航空航天大学宇航学院，北京 100191;2.中国航天科工集团北京机电工程总体设计部，北京 100854)

0 引言

结构优化作为现代结构设计方法，广泛用于航空、航天、船舶等各个领域。通常把结构优化按照设计变量的类型分划为3个层次:结构尺寸优化、形状优化和拓扑优化［1］。三者分别对应于不同的设计阶段，即详细设计阶段、基本设计阶段与概念设计阶段。结构拓扑优化是结构优化领域的前沿研究课题，通过改进结构的拓扑形式，可大大提高结构的性能，或减轻结构的重量。

拓扑优化按照研究的结构对象可分为离散体结构拓扑优化(如桁架、刚架、加强筋板、膜等骨架结构及它们的组合)和连续体结构拓扑优化(如二维板壳、三维实体)两大类［2］。目前，连续体结构拓扑优化已经相对成熟，研究较多的方法主要有均匀化方法、变厚度法、变密度法及进化结构法等［3］。连续体结构拓扑优化已在许多工程领域得到应用，如用于导弹结构［4］和飞机结构［5－7］的设计上。随着计算机技术的发展，产生了一系列可辅助进行结构拓扑设计的软件，Altair公司的OptiStruct就是其中之一。

折叠翼能缩小导弹和发射装置的尺寸，节省储运空间，便于箱式贮装、运输和发射，增加车辆、舰艇或飞机的运载能力，提高战斗力，因而在国防上得到了广泛应用［8］。由于这类飞行器对结构质量、刚度和强度都有较高的要求，常规的设计方法是依据工程师的设计经验，通过一系列设计-校核-修改的循环，最终设计出满足要求的结构。这种设计方法耗时耗力，且需工程师有一定的设计经验。因此，通过对折叠翼结构进行拓扑优化，以寻求具有最佳传力路径的结构布置形式，对飞行器的设计有着重要的指导意义。

本文基于Altair公司的HyperWorks软件平台，对某折叠翼的翼梢结构进行拓扑优化设计。首先，利用其前处理软件HyperMesh进行优化问题的建模，该优化问题包含翼梢结构的拓扑设计变量和蒙皮厚度设计变量;然后，应用其优化求解器OptiStruct进行求解;根据得到的结构拓扑对翼梢结构进行设计，并进行分析校核，得到满足结构质量、刚度和强度要求的结构。通过拓扑变量和尺寸变量的混合优化，有助于得到较优的翼梢结构。

1 折叠翼结构优化设计问题描述及有限元模型

某折叠翼的结构形式如图1所示，翼根内部有折叠机构和锁紧机构;当翼面从折叠状态到展开状态后，锁紧机构作动，将一锁紧件推入连接件，使翼根和连接件连在一起，从而使翼面锁定在展开状态。翼梢、翼根和连接件均采用钛合金材料(材料参数为:弹性模量E=123 GPa，泊松比 ν=0.33，密度 ρ=4 650 kg/m3，屈服极限σs=1 070 MPa)，支撑轴和锁紧件均采用45Cr材料。根据设计要求，除去锁紧机构、翼根、连接件和支撑轴的质量后，要求翼梢部分质量不超过3.2 kg;此外，要求梢部最大位移不超过4 mm，设计的结构性能指标与设计要求之间允许有10%的容差。

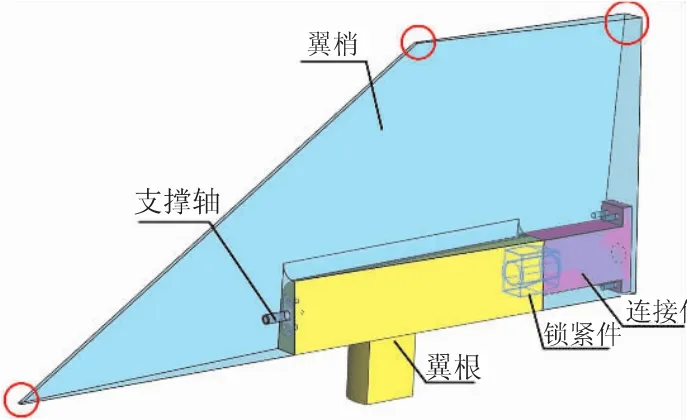
图1 折叠翼结构形式Fig.1 The structure of folding wing

基于HyperMesh建立折叠翼结构的有限元模型，为减少概念设计的计算量，实体采用四面体单元，平板采用三角形单元。翼梢单元尺寸为5 mm，其他部件单元尺寸为2 mm，有限元模型的单元总数为136 937。由于折叠翼各部件不是一个整体结构，力是通过各部件的接触面传递的，故通过定义两部件之间的接触来正确模拟折叠翼的展开状态。折叠翼的有限元模型如图2所示。约束翼根底端各个节点的3个平动自由度，施加在翼面上的等效均布压力为0.149 MPa。

2 优化问题的数学模型与求解

变密度法SIMP(Solid Isotropic Microstructure with Penalization for intermediate densities)是目前应用最多的连续体结构拓扑优化方法。SIMP通常以单元相对密度为设计变量，将连续体结构拓扑优化由0～1整数优化问题转变为一个连续变量的优化问题。SIMP法使用最多的插值模型为密度-刚度幂次关系模型，即规定单元弹性模量与单元密度存在指数变化关系:

式中 xi为单元的相对密度(0≤ xi≤1);p为惩罚因子;E0和E分别为惩罚前和惩罚后的弹性模量。

图2 折叠翼有限元模型Fig.2 The FEA model of folding wing

通过设定一个大于1的惩罚因子p(惩罚因子的取值应在3～5之间)，可对中间密度单元的刚度矩阵进行惩罚，从而达到减少中间密度单元，获得近似离散设计结果的目的。

在进行概念设计时，本文将翼梢部分作为拓扑设计区域，同时将翼梢外表面蒙皮厚度作为一个设计变量。把拓扑变量和尺寸变量结合在一起，同时进行优化，可得到最优的翼梢内部结构形式和最优的外部蒙皮厚度，从而得到最优的整体式结构。

针对翼梢结构设计，本文采用SIMP建立一个包含拓扑变量和蒙皮厚度变量的结构优化问题，其数学形式可表述如下:

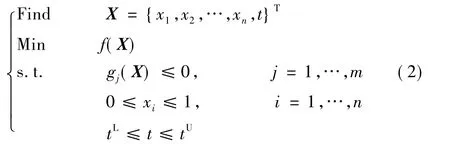
其中，X为连续变量;xi为拓扑变量即单元相对密度;n为拓扑变量个数;t为外表面蒙皮厚度变量;tL为厚度下限;tU为厚度上限;f(X)为优化目标函数，本文以结构的应变能作为优化目标，如式(3)所示;gj(X)为第j个结构性状约束;m为约束个数，包含结构质量约束、单元应力约束和节点位移约束，如式(4)所示。

式中 f(X)为结构总应变能，即柔顺度或柔度;F和U为有限单元的节点力和位移矢量;K为优化前的总刚矩阵;N为结构的总单元数;ki为单元刚度矩阵;k0为拓扑设计区域单元无惩罚的单元刚度矩阵。

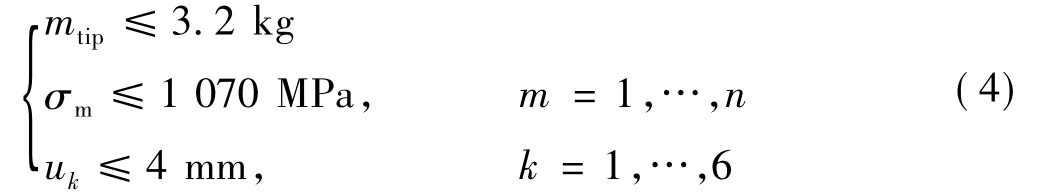
式中 mtip为翼梢质量;σm为单元的Mises应力;uk为翼梢前缘和外缘边缘的6个节点(图1中圆圈中的节点)位移的模。

根据式(2)在HyperMesh中建立优化模型，以翼梢区域单元的相对密度和蒙皮厚度作为设计变量，设蒙皮厚度下限tL=0.1 mm，上限tU=3 mm，以结构应变能最小为设计目标，并定义式(4)中所示的约束。设惩罚因子p=3，定义沿翼中面法线方向的脱模约束。利用优化求解器OptiStruct进行求解。OptiStruct采用局部逼近的方法求解优化问题，即利用敏度信息得到近似模型，然后求解近似模型［9］。经过30步的迭代，得到翼梢的最优拓扑形式，应变能的迭代曲线如图3所示，最优解对应的应变能值为12 593.89 N·mm。优化的过程数据显示，最优解下的结构有6.7%的约束违反量，即翼梢后缘节点的位移为4.266 mm，超过要求的4 mm，但在容差的允许范围内。

得到的最优翼梢结构单元相对密度分布，即结构的材料分布如图4所示。可直观看出中间密度的单元较少，材料分布有明显的界限，这有利于将结果转化为实际结构;最优蒙皮厚度为1.982 mm，圆整为2 mm。

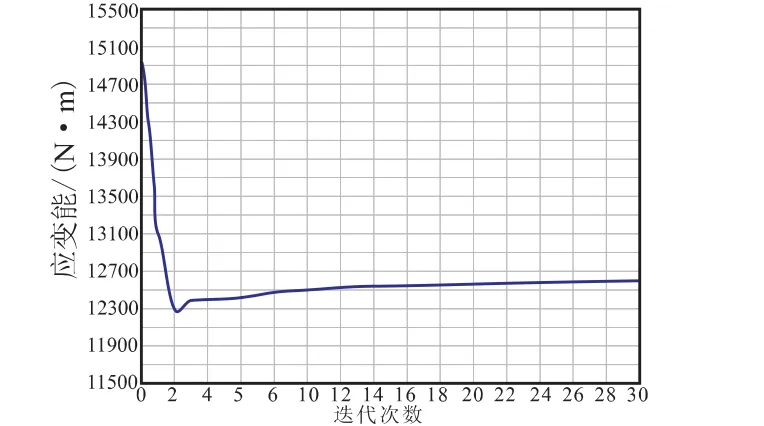
图3 目标函数(结构应变能)迭代曲线Fig.3 Variable trend of the objective function

图4 翼梢结构的最优拓扑形式Fig.4 The topology optimization form of folding wing tip

根据优化得到的最优拓扑形式，对翼梢结构进行设计。考虑以下因素:(1)从拓扑优化得到的结构含有中间密度材料，需要去除;(2)如果按照拓扑得到的结构材料分布，其无材料填充区域边界的形状较复杂，这会增大加工的难度，因此需对最优拓扑进行简化，以适应加工要求;(3)结构需要维持翼面形状，以满足气动外形的要求。综合考虑上述3个因素，设计的整体式结构的翼梢剖面如图5所示。表面蒙皮厚2 mm，内部根据拓扑形式去除一些材料。设计的翼梢结构质量为3.197 kg，满足结构质量要求。

3 结构校核

为验证设计的翼梢结构是否满足结构的刚度和强度要求，对根据拓扑优化结果设计的翼梢结构(如图5所示)重新进行建模，并进行分析。翼梢以实体导入有限元模型，所以部件均采用四面体单元，单元尺寸均为2 mm，有限元模型的单元总数为458 491。载荷工况与优化设计时的载荷工况一致，即折叠翼翼面受均布压力0.149 MPa，固定翼根底部。与优化的有限元模型一样，定义各个部件之间的接触。静力分析得到的位移云图如图6所示，翼梢的最大位移为4.293 mm，超过4 mm，但在容差范围之内，可接受;VonMises应力云图如图7所示，最大应力为610.1 MPa，位置在翼梢和翼根接触面上，最大应力值在强度极限内，且有较大的安全裕度，结构是安全的。设计的结构在该静力工况下的总应变能为12 141.59 N·mm。

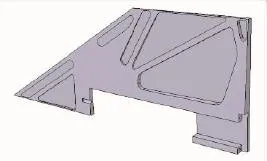
图5 根据最优拓扑设计的翼梢结构Fig.5 The structure of wing tip according to the optimal topology design

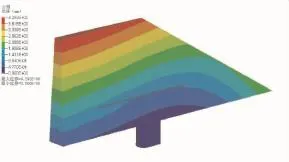
图6 折叠翼在均布压力下的位移云图Fig.6 Displacement of folding wing under uniform external pressure

图7 折叠翼在均布压力下的VonMises应力云图Fig.7 VonMises stress of folding wing under uniform external pressure

从上述结果可见，根据最优拓扑形式设计出来的结构符合质量、刚度和强度要求，设计结构是合理的。

4 结论

(1)将结构拓扑优化方法用于折叠翼翼梢结构的设计是有效的，拓扑优化得到的最优拓扑形式可为翼梢结构的设计提供了一定依据。然而，为了适应加工要求，需对拓扑形式进行一定的转化，这一过程的主动性较强。后续将针对折叠翼结构开发将拓扑优化结果自动转化为实际可用结构的模块，以便于结构设计。

(2)将蒙皮厚度作为设计变量，与翼梢的拓扑同时进行优化，有助于得到更好的结构形式，而且基于HyperWorks软件，可方便求解该问题。在进行结构设计时，也可将结构尺寸作为设计变量参与优化，这样的混合变量优化会更有利于设计。

(3)本文仅考虑了静力工况下的结构优化，设计完结构需对动力学工况进行校核;如果考虑动力工况下的拓扑优化，会使结构更具有实际意义。

［1］程耿东.受应力约束的平面弹性体的拓扑优化［J］.大连理工大学学报，1995，35(1):1-9.

［2］左孔天.连续体结构拓扑优化理论与应用研究［D］.武汉:华中科技大学，2004.

［3］叶红玲，隋允康.应力约束下三维连续体结构拓扑优化分析［J］.力学(季刊)，2006，27(4):621-627.

［4］Luo Zhen，Yang Jing-zhou，Chen Li-ping.A new procedure for aerodynamic missile design using topological optimization approach of continuum structures［J］.Aerospace Science and Technology，2006，10(5):364-373.

［5］Gred Schuhmacher，Martin Stettner，Rainer Zotemantel，et al.Optimization assisted structural design of a new military transport aircraft［C］//10th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference，Albany，New York，2004.

［6］王伟.机翼结构拓扑优化的一种新渐进结构优化方法［J］.飞机设计，2007，27(4):17-20.

［7］邓扬晨，张卫红，章怡宁.基于分级优化的飞机翼面结构布局综合技术研究［J］.强度与环境，2005，32(1):27-35.

［8］李莉，任茶仙，张铎.折叠翼机构展开动力学仿真及优化［J］.强度与环境，2007，34(1):17-21.

［9］张胜兰，郑冬黎，郝琪，等.基于HyperWorks的结构优化设计技术［M］.北京:机械工业出版社，2007.