应变率对复合材料壳体外压性能的影响①

侯 晓，秦 谊，何高让，王凌云

(1.中国航天科技集团公司四院，西安 710025;2.中国航天科技集团公司四院四十一所，固体火箭发动机燃烧、热结构与内流场国防科技重点试验室，西安 710025)

0 引言

潜射导弹在水下高速运行时，弹体表面会产生空泡，当导弹穿越水面时，因介质突变，空泡发生溃灭，引起导弹力学环境急剧变化。空泡溃灭时间约为5 ms［1］，复合材料壳体在此过程中受到冲击外压载荷的作用。国内外学者对复合材料壳体的外压稳定性问题进行了广泛的研究。Smerdov［2］基于经典薄壳理论通过对铺层角度进行优化，提出提高复合材料壳体外压载荷的方法。Han等［3］基于一阶剪切理论研究了对称铺设圆柱壳在侧向外压和静水外压载荷作用下的屈曲特性。杜建科等［4］采用非线性屈曲理论，在不考虑几何缺陷和材料缺陷的条件下，利用ANSYS软件对纤维缠绕复合材料壳体和燃烧室侧压稳定性进行了对比计算。Ouellette等［5］给出了纤维缠绕材料圆管在侧向压力作用下的屈曲荷载计算方法，指出对复合材料圆柱壳结构进行外压屈曲分析时必须考虑初始几何缺陷的影响。周承倜等［6］使用能量法和有限差分法分析了多层复合材料圆柱薄壳在静水压力作用下的屈曲性能，考虑了初始几何缺陷、几何非线性和材料的物理非线性等因素对临界载荷的影响。王永志等［7］对复合材料旋转壳的失稳问题进行了有限元推导，考虑了横向剪切变形的影响，认为横向剪切变形对复合材料构件的结构稳定性影响较大。李志敏［8］运用了边界层理论对纤维增强各向异性层合剪切圆柱壳的屈曲进行了分析，分析中同时考虑了前屈曲非线性变形，后屈曲大挠度和初始几何缺陷的影响以及横向剪切变形和耦合刚度的影响。这些研究都是针对准静态外压载荷进行的研究，对作用时间按毫秒等级计量的外压载荷来说，还需考虑加载速率的影响。

对大部分材料而言，载荷的加载速率对材料的力学性能均有不同程度的影响，一般用应变率来描述。周元鑫等［9］研究了不同应变率下石墨纤维增强铝合金基体复合材料的拉伸性能，研究结果表明该材料具有明显的应变率强化效应。陈思颖等［10］研究了炭纤维、玻璃纤维和Kevlar纤维的拉伸力学性能的应变率相关性进行，结果是几种纤维的弹性模量无一例外地随应变率的增大而增大。蒋邦海等［11－12］对炭纤维增强复合材料试件的应变率相关性进行了试验和研究，结果表明复合材料的强度性能不但存在应变率效应，而且这种效应是各向异性的。

目前，对固体火箭发动机复合材料壳体外压承载能力的研究都在准静态加载条件下进行，对其动态力学性能的研究较少。按照类似的原理，复合材料壳体对动态外压载荷的承载能力应高于静态外压承载能力，如果能够得到复合材料壳体应变率与外压载荷定量或定性相关关系，按壳体动态外压承载能力进行设计，可减轻复合材料壳体的质量，提高发动机质量比。正是基于这一考虑，本文对复合材料壳体外压载荷承载能力与应变率的相关关系进行了试验和分析。

1 试验件和试验方法

1.1 试验件设计

按相同设计和工艺状态研制了9台试验件，其中3台进行静态外压试验，6台进行动态外压试验。试验件赤道间距200 mm，直径 φ200 mm，壁厚1.6 mm，前后裙采用了铝合金材料，试验件结构如图1所示。

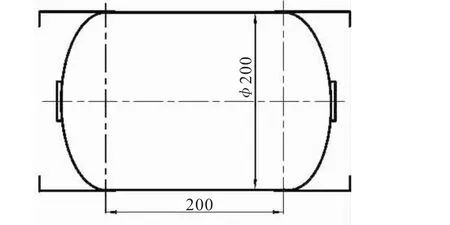
图1 复合材料壳体试验件Fig.1 Composite case sample

1.2 试验方法介绍

如图2所示，将试验件置于 φ350 mm ×550 mm的试验容器内，试验件一端与试验容器固支连接，另一端用堵盖密封。向容器内注入水介质，通过手动压力泵和航天四院设计的脉冲压力发生器向容器内加载静态外压和脉冲外压，手动压力泵上连接观察用压力表。试验件表面粘贴有应变片，试验容器壁上安装测压传感器。

静态外压试验时，系统的采集频率设定为10 Hz;动态外压试验时，系统的采集频率设定为2 000 Hz。要求静态外压试验在3～5 min内完成，脉冲外压发生器具有在200 ms内达到1 500 kPa以上的能力(估算值)。试验现场环境气压为98 kPa。

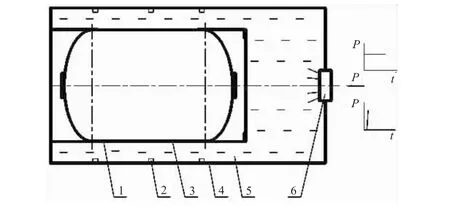
图2 外压试验装置Fig.2 Expermental system of external pressure

2 静态外压承载能力计算

试验过程中实际对试验件施加了轴外压载荷。首先利用公式法对该试验件的静态轴外压承载能力进行计算。根据文献［13－15］，理论临界失稳外压按式(1)计算，理论临界失稳轴压按式(2)计算。该试验状态下壳体同时受轴外压联合载荷的作用，应满足式(3)关系。

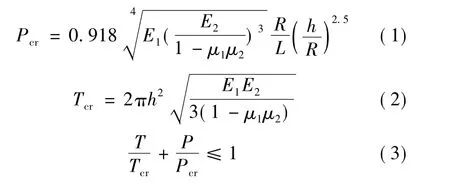
式中 E1、E2分别为壳体纵、环向弹性模量;μ1、μ2分别为纵、环向泊松比;R、h、L分别为壳体直径、壁厚和赤道间距;T、P分别为壳体实际承受的轴压和外压。

联立式(1)～(3)，参数T用加载压强表示，代入试验件的设计参数，求得壳体的最大失稳压强为631 kPa。该计算值为理论值，根据文献［14－15］，由于材料缺陷和几何缺陷等原因，采用线性理论导出的理论临界应力计算公式不能直接用于工程实际，必须进行修正。文献［14］根据实际试验结构给出钢圆筒临界外压计算时的修正系数为0.8。复合材料的均匀性比钢材料差，修正系数应选取的更低一些。文献［15］中复合材料壳体临界轴压计算时修正系数应按0.3～0.5选取。本试验中试验件的制作要比一般的工程结构件精细，修正系数更高一些。试验中主要加载载荷为外压载荷，综合考虑，修正系数取0.72，则计算临界失稳压强为454 kPa。

3 静态外压试验

在静态外压试验初始加载阶段，随载荷增加，压力表读数逐渐增大;当载荷加载到一定值后听到复合材料破坏的响声，同时压力表的压力值达到最大;继续加载，压力值开始下降。由此判断试件破坏，试验终止。

3台试验件的试验结果见表1。表1列出了测试压强(绝压)和相对压强(平衡大气压强后试件的实际承载压强)。No.2试件的相对压强与计算结果相同，No.1、No.3试件的试验结果均略小于计算结果，说明修正系数的选取略高。

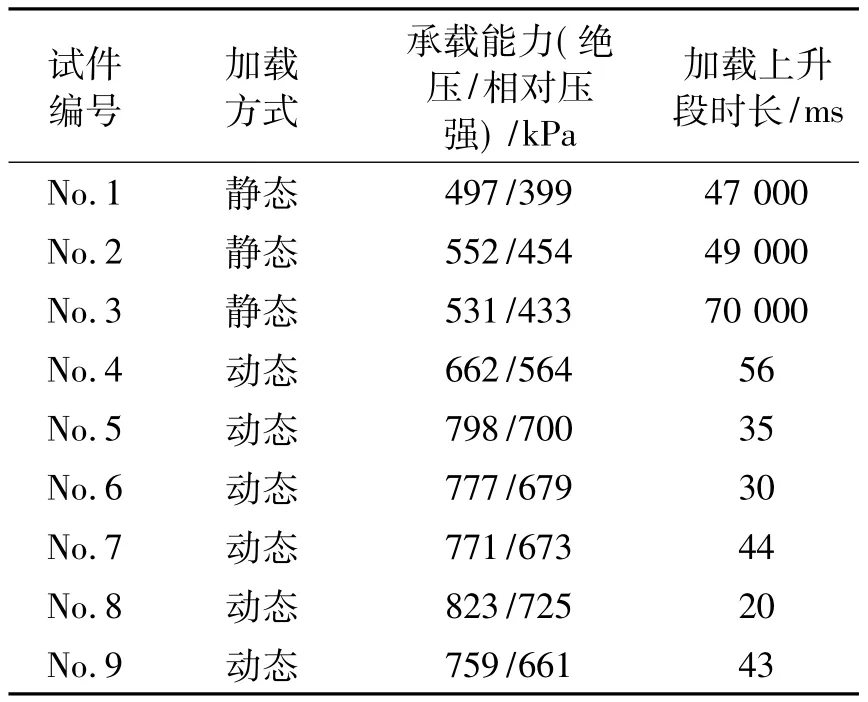
表1 静、动态外压试验结果Table 1 The results of external pressure in static and dynamic condition

图3为3台壳体静态轴外压试验测试系统加载曲线。由图3可见，初始加载阶段试件表面载荷按抛物线上升，到最大值时加载源虽然仍继续加载，但测试压强开始下降。测试系统曲线与试验现场压力表监视结果一致。压强下降的原因是由于壳体外压失稳后卸压所致。加载曲线开始下降的时刻即为失稳破坏时刻，对应载荷为壳体失稳破坏载荷。

图4为No.3试件部分测点应变测试结果(No.1、No.2试件测试结果类似)。由图4可知，在第68 s时刻壳体局部应变快速增加，70 s时刻部分点达到最大值。由于加载源仍在继续，其中一点应变继续增大，表明该点所在部位出现了较大变形，试验后解剖证实该点对应部位破坏。应变测试结果表明，该试件在70 s时刻开始失稳，74 s时刻完全失稳破坏，完全失稳破坏时的最大应变在－3 600 με左右。

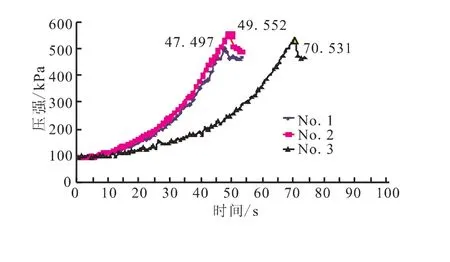
图3 静态外压载荷-时间曲线Fig.3 External pressure-time curves in static condition

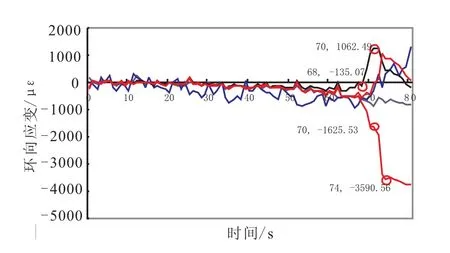
图4 No.3应变测试曲线Fig.4 Strain curves of No.3 sample

由以上加载和应变测试曲线分析知，3台壳体的破坏值分别为 399、454、433 kPa，加载时长为 47、49、70 s，均可视为准静态加载。

4 动态外压试验

动态外压试验时，冲击外压加载系统可实现10～200 ms脉冲外压加载。

4.1 空载调试

动态外压试验前首先进行空载调试。空载调试的目的是为了确定加载载荷随时间变化的趋势以及加载源所能提供的最大加载压强，试验得到的加载载荷－时间曲线见图5。由图5可知，该试验条件下加载载荷为一脉冲波形，峰值载荷绝压可达到1 864 kPa，去除环境压强影响后，实际加载压强为1 766 kPa，可满足加载要求。

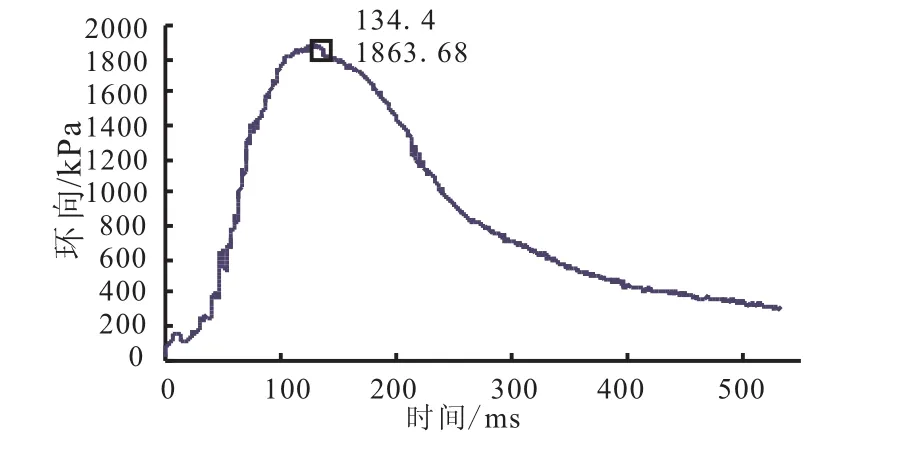
图5 空载试验载荷-时间曲线Fig.5 Load-time curve of the no-load test

4.2 负载调试

为保证试验条件的完全一致，排除加载容器内不同储水量对试验结果的影响，正式试验前又进行了带试件的调试试验。调试试件的外形几何尺寸与正式试件完全相同，但将壳体的壁厚设计的较厚，刚性较大，调试试验结果见图6。由图6可知，带试件状态下，加载载荷也为一脉冲波形，峰值最大绝压压强可达到1 761 kPa，去除环境压强影响后，实际加载压强为1 663 kPa。

空载调试和负载调试时，加载载荷都可达到静态试验值的3倍以上，可满足试验条件。

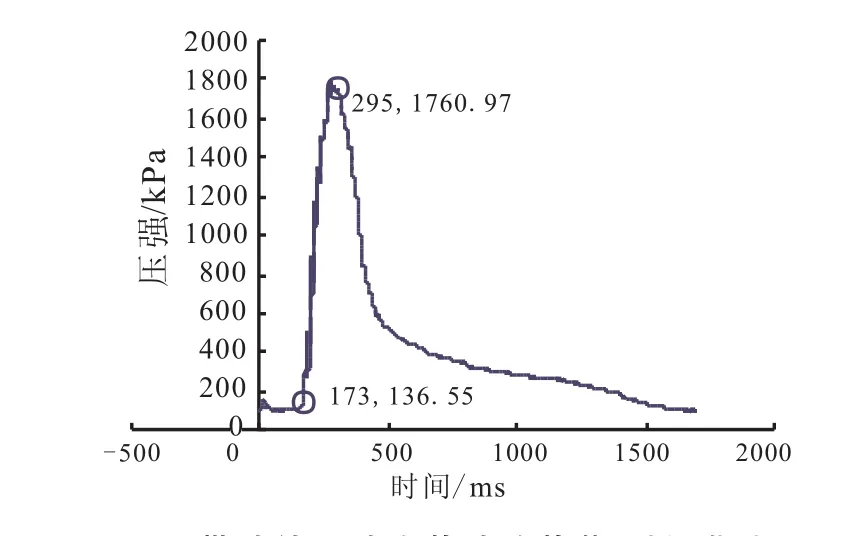
图6 带试件调试空载试验载荷-时间曲线Fig.6 Load-time curve of the test with sample

4.3 正式试验

按照调试试验的状态对6台正式产品进行了动态外压试验，试验结果见表1，加载载荷-时间曲线见图7。

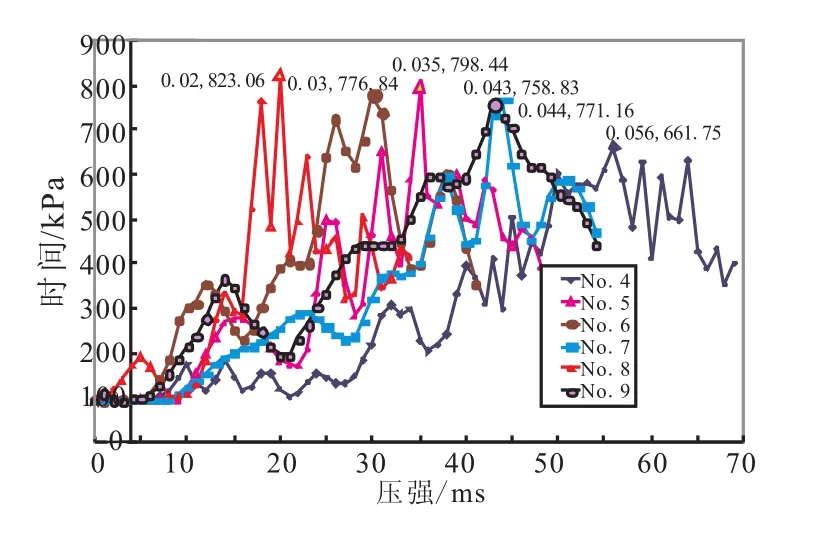
图7 动态外压载荷-时间曲线Fig.7 External pressure-time cures in dynamic loads test

从图7看出，6次试验中，加载载荷均为脉冲压强波，实际加载压强为564～725 kPa(相对压强)，低于调试试验值1 663 kPa，也低于空载调试试验值1 766 kPa。对比空载调试和相同几何尺寸试件调试结果分析知，冲击加载系统提供的能量远高于壳体试件的实际承载能力，当加载载荷不断上升并达到壳体试件的临界外压时，壳体开始失稳并释放了一定的空间，测试压强曲线开始下降，其变形过程与静态外压试验时相同。从以上分析知，图7中各试件加载峰值点载荷即为试件的动态外压承载能力，试验平均值为667 kPa。6台壳体加载载荷上升很快，以计时时刻计算，加载上升段时间为20～56 ms，基本达到了快速加载的目的。

试验过程中对应变进行了测试，图8为No.7壳体应变测试结果，其他壳体基本类似。从图8可看出，对应载荷曲线峰值点44 ms时刻部分测点的应变趋近于最大值，部分测点的应变值继续增大，表明该时刻壳体对应部位破坏。

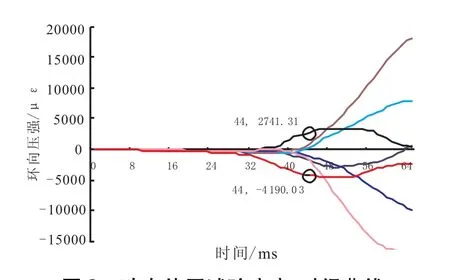
图8 动态外压试验应变-时间曲线Fig.8 Strain-time curve in dynamic loads test

5 试验结果分析

5.1 失稳应变的确定

外压试验中(存在附加轴压)，复合材料壳体的主要破坏形式是失稳破坏，因此对应变的分析应以负应变为准。动态加载过程中，部分应变测点的测试值(负应变)持续上升，然后在－4 000 με左右完全失稳破坏。静态加载时由于手动泵加载方式为间歇式加载，完全失稳时刻的最大应变与开始失稳时相差2 s。动、静态外压试验过程中完全失稳破坏的应变在－4 000 με左右。

5.2 应变率的确定

动态试验过程中6台试验件载荷上升段时间为20～56 ms，其中20 ms和56 ms各出现1次，其他均在30～44 ms之间。按平均加载时间38 ms计算，应变按前述 －4 000 με 计算，则应变率为 0.105 s－1。

5.3 应变率对承载能力的影响

从动、静态外压试验对比结果看，复合材料壳体试验件动态轴外压承载能力明显高于静态时的承载能力。承载能力提高的原因是由于材料的模量具有应变率相关性。

取3台静态试验壳体相对压强均值429 kPa作为该壳体在准静态轴外压载荷作用下的承载能力，取6台动态试验壳体相对压强均值667 kPa作为该壳体在动态轴外压载荷作用下的承载能力，则当应变率为0.105 s－1时，承载能力由 429 kPa 提高到 667 kPa，动态加载下承载能力是静态下1.55倍。

6 结论

(1)复合材料壳体的外压(同时加载了附加轴压)承载能力具有应变率相关性，应变率提高，承载能力相应增加。

(2)用静态试验结果评判壳体对冲击类载荷的承载能力是不恰当的，承受动载荷作用的结构，应以相应载荷条件下的试验结果为依据，否则将造成结构的冗余设计，降低效率。

(3)试验证明，直径200 mm、壁厚1.6 mm的复合材料壳体，当应变率达到达到0.105 s－1等级时，承载能力是静态环境下的1.55倍。

［1］罗金玲，毛鸿羽.导弹出水过程中气/水动力学的研究［J］.战术导弹技术，2004(4):23-25.

［2］Smerdov A A.A computational study in optimum formulations of optimization problems on laminated cylindrical shells for buckling II－ Shells under external pressure［J］.Composites Science and Technology，2000，60:2067-2076.

［3］Han B，Simitses G J.Analysis of anisotropic laminated cylindrical shells subjected to destabilizing loads，Part II:numerical results［J］.Composite Structures，1991，19:183-205.

［4］杜建科，田晓耕，沈亚鹏，等.复合材料燃烧室均布侧压下稳定性分析［J］.固体火箭技术，2002，25(2):18-21.

［5］Ouellette P，Hoa S V，Sankar T S.Buckling of composite cylinders under external pressure［J］.Polymer Composites，1986，7:363-374.

［6］周承倜，周建平.多层复合材料圆柱壳的非线性失稳计算［J］.应用数学和力学，1986，7(1):17-23

［7］王永志，向锦武.复合材料旋转壳稳定性有限元分析和横向剪切变形的影响分析［J］.复合材料学报，2006，23(4):175-179.

［8］李志敏.船舶与海洋工程中复合材料圆柱壳结构屈曲和后屈曲行为研究［D］.上海交通大学，2008.

［9］周元鑫，张学峰，夏源明.应变率对Gr/Al金属基复合材料力学性能的影响［J］.爆炸与冲击，1999，19(3):243-249.

［10］陈思颖，黄晨光，段祝平.几种高性能纤维束的冲击动力学性能试验研究［J］.爆炸与冲击，2003，23(4):355-359.

［11］蒋邦海，张若棋.一种炭纤维织物增强复合材料应变率相关的各向异性强度准则［J］.爆炸与冲击，2006，26(4):333-338.

［12］蒋邦海，张若棋.动态压缩下一种炭纤维织物增强复合材料的各向异性力学性能试验研究［J］.复合材料学报，2005，22(2):109-115.

［13］陈盛秒.外压容器涉及的公式法及其应用［J］.压力容器，2008，25(11):30-33.

［14］黄启珍，等.导弹结构·材料·强度(下)［M］.北京:宇航出版社，1996.

［15］陈汝训.复合材料壳体的轴压稳定性［J］.固体火箭技术，2001，24(1):13-15.