永磁直线同步电机无位置传感器动子位置辨识

王利， 卢琴芬， 叶云岳

(浙江大学电气工程学院，浙江杭州 310027)

0 引言

直线电机可以将电能直接转变为直线运动的机械能，省去了齿轮、链条等中间传动机构，可以极大地简化系统结构，降低传动损耗［1］。其中永磁直线同步电机具有体积小、推力密度高等优点，因而广泛应用于伺服控制系统中。

交流调速系统中，为了实现高精确度的速度和位置控制，常采用矢量控制或者直接转矩控制。无论哪种控制方式，都需要高精确度的电机速度和位置信息，这些信息通常由光电编码器、测速发电机、旋转变压器等传感器获取。直线电机一般使用直线光栅检测动子速度和位置，加装这些传感器增加了系统的成本和复杂性，降低了系统的机械抗干扰能力，而且速度和位置传感器对安装环境要求较高，比如直线光栅对安装面的平整度要求非常高［2］。

针对机械式的位置和速度传感器在某些应用场合受限的情况，近些年研究人员提出了多种无位置传感器旋转电机转子位置估算方法。如基于反电势的反电势观测法，基于永磁同步电机凸极效应的高频信号注入法，基于状态观测器的自适应观测器法和卡尔曼滤波器法等［3－7］。基于反电势的转子位置估算方法的优点是计算量小，易于实现，但是电机低速运行时反电势很小，而且转子磁链对定子阻抗变化敏感，导致该方法在低速运行时的电机转子位置估算精确度有所下降。高频信号注入法基于电机的凸极效应(固有凸极或饱和凸极)估算转子位置，这种方法要求电机的凸极效应比较明显，对于表贴式一类凸极效应不明显的隐极电机，该方法的转子位置估算精确度不理想，此外高频信号注入法还需要额外的滤波器，滤波器的设计是高频信号注入法应用的难点。基于状态观测器的方法具有较好的鲁棒性，不过实时计算量大，动态性能差于前两者。

基于磁链变化的转子位置检测方法是反电势观测法的延伸，也可称为反电势积分法，这种方法同样具有易于实现的优点，不过在低频下转子(直线电机为动子)位置估算结果容易受到干扰［8］。直线电机一般在较低的频率下即可达到较高的直线速度，所以大多数直线电机伺服系统实际运行频率都比较低，反电势比较小，这增大了反电势积分法应用时有效信号的提取难度，目前对该算法的研究大多数还是针对较高运行频率的直线电机［9－11］，如何提高直线电机低频运行时的动子位置估算精确度是反电势积分法研究的重点和难点。

本文针对空心式永磁直线同步电机的动子位置和速度估算进行研究，对直线电机低速运行时出现的磁链漂移问题进行分析，通过磁链中值和死区补偿算法有效解决了反电势积分引起的磁链漂移问题，提高了直线电机低速运行时的动子位置估算精确度，最后分析了电机参数变化对动子位置估算精确度的影响。

1 基于反电势积分的动子位置估算算法

在α－β静止坐标系下，永磁同步电机的电压方程［12－14］为

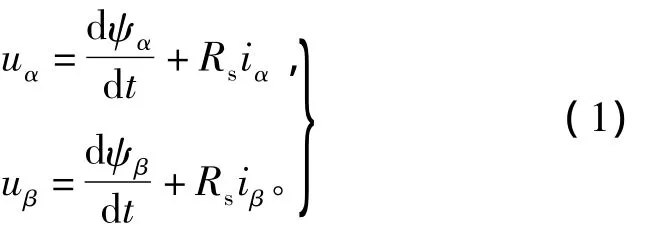
磁链方程为

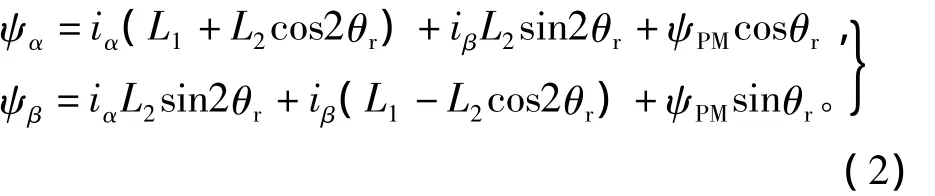
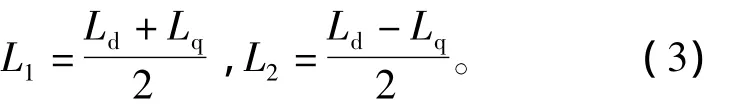
式中:uα、uβ，iα、iβ，ψα、ψβ分别为定子电压，电流和磁链在α－β坐标系下的分量;Rs为定子电阻;ψPM为永磁体磁链;Ld、Lq为定子绕组的d、q轴电感;θr为动子位置。

对于隐极式永磁直线电机，L2≈0，定子电压方程可以简化为

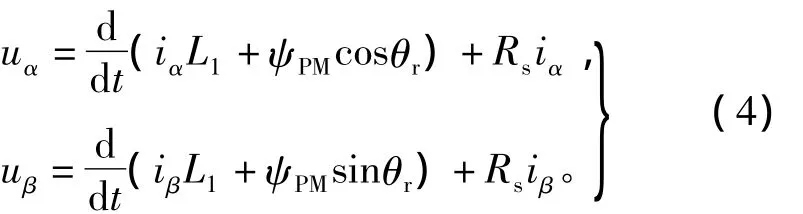
定义L1和L2分别为

定子磁链则可表示为

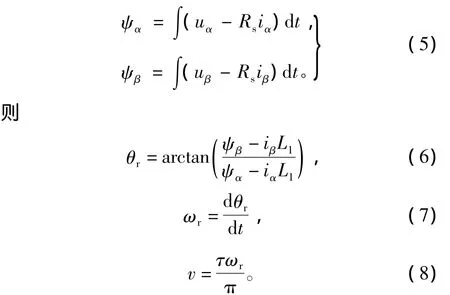
式中:ωr为角速度;v为速度;τ为电机极距。

2 永磁直线电机矢量控制

矢量控制是应用最为广泛的永磁同步电机控制策略，其中采用转子磁场定向的矢量控制可以实现转矩电流分量和励磁电流分量的解耦控制。矢量控制的类型包括id=0控制，最大转矩电流比控制，cosφ=1控制等，其中id=0矢量控制的思想就是使定子电流中只含交轴分量，这种控制方法具有算法简单、转矩性能好等优点，广泛应用于电机调速系统中。

图1为无位置传感器矢量控制原理图，PMLSM为空心式永磁直线同步电机，采用id=0的动子磁场定向矢量控制策略，实现电流，速度双闭环控制。动子位置信息由动子位置估算器获得。速度偏差作为速度调节器的输入，速度调节器的输出作为电流调节器的输入，电流调节器的输出经过空间矢量脉宽调制(space vector pulse width modulation，SVPWM)得到三相全桥各个全控管的开关状态，由此驱动智能功率模块(intelligent power modules，IPM)输出幅值和频率可调的斩波电压，使直线电机跟随指定速度运动。

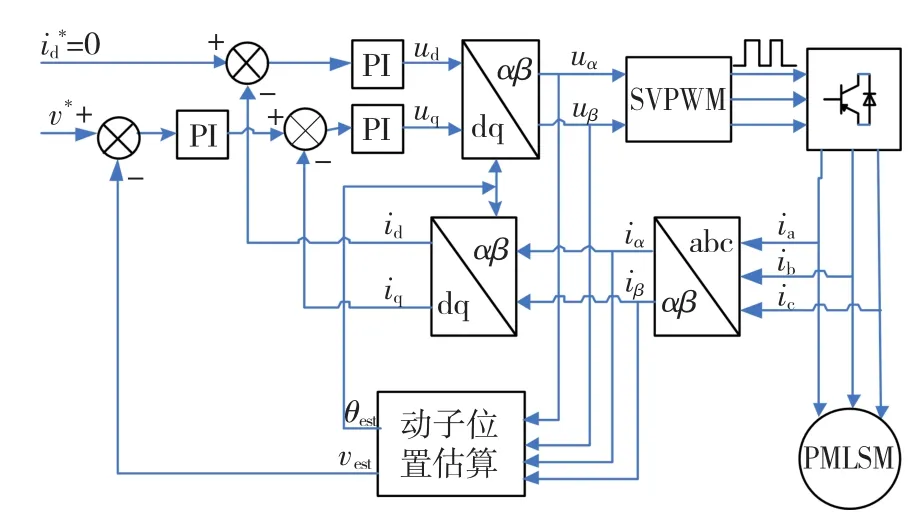
图1 永磁直线电机无位置传感器矢量控制系统Fig．1 PMLSM sensorless vector control system

3 实验及结果分析

3．1 实验平台

实验电机为空心式圆筒永磁直线电机。电机电感Ld=16 mH，Lq=18.5 mH，电枢相电阻Rs=15.82 Ω，极距τ=0.025 5 m，反电势常数为30 V/(m/s)，推力常数为90 N/A。电流传感器采用LEM公司的LTS 6－NP，选择量程范围为－3～3 A。功率模块为三菱DIPIPM－PS21564(15 A/600 V)。控制芯片采用TI的TMS320F28335浮点处理器。

3．2 磁链零漂的抑制

磁链由反电势积分获得，而开环反电势纯积分会带来积分漂移的问题，反电势信号中很小的直流分量都可能使积分器输出达到饱和。直流分量可以通过高通滤波器滤除，但是由于直线电机大多在低频下运行，很难设计恰当的高通滤波器只滤除直流分量而对实际的磁链不产生衰减，此外滤波器带来的信号延迟问题很难解决。针对直线电机的特殊性，本研究采用磁链中值法消除磁链漂移，具体实现方法为统计上个电机运行周期的磁链中值，实际磁链为反电势积分得到的磁链与上周期的磁链中值的差值，可以用式(9)描述这一过程，即

式中:ψint为反电势积分得到的磁链初始值;ψmean为磁链中值。

利用DSP统计上个电机运行周期的磁链最大值和最小值，两者的平均值即为磁链中值。设置电流采样频率为载波频率，磁链统计个数N应当满足

式中:fc为载皮频率;fr为调制波频率。

调制波频率和速度相关，由直线电机速度公式可知

式中vref为给定速度。实际程序中指定速度都需要经过斜坡函数处理，所以这里的给定速度为斜坡函数的输出速度。

磁链零漂消除结果如图2所示。图2中，ψαint为积分得到的初始磁链，ψα为采用磁链中值法处理之后的磁链结果。

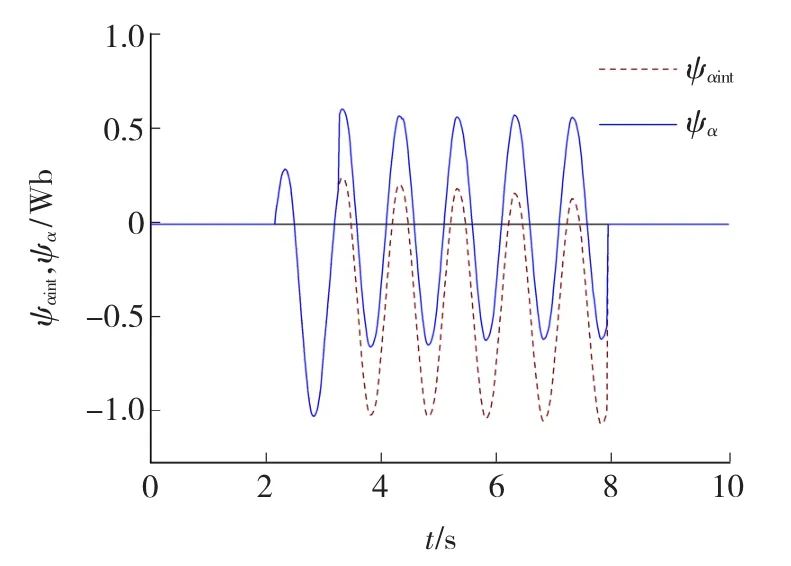
图2 消除磁链漂移Fig．2 Elimination of flux linkage drift

通过多次实验发现，低频下磁链漂移均是逐渐增大或逐渐减小的，说明系统中直流扰动分量具有一致性，对于这种具有趋势性的磁链变化，经过一次磁链中值消除积分漂移之后得到的磁链关于零轴不对称，需要经过第二次磁链中值消除零漂，经过两次磁链中值消除积分零漂后，才可使磁链关于零轴对称。

由于两次采用中值法消除反电势积分后的磁链零漂，系统在前两个运行周期处于两个磁链中值的统计过程，输出磁链误差很大，此时的计算结果不可使用。因为在零速下无反电势，所以基于反电势积分的动子位置估算算法需开环启动，而磁链中值的初始化在开环启动过程中即可完成，对后续的速度闭环时动子位置计算无影响。

在磁链漂移趋势很大的系统中，采用两次磁链中值法消除磁链漂移在每周期磁链中值切换时刻都会产生磁链输出跳变，如图3中的虚线框所示。图3中，ψint为积分得到的磁链初始值，ψout1为经过第一次磁链中值法之后的磁链输出结果，ψout2为经过第二次磁链中值法之后的磁链输出结果。磁链跳变是因为磁链漂移趋势变化较大，导致磁链中值的明显变化，而磁链中值是周期性更新的，这样在磁链中值更新时刻必然导致输出磁链的畸变。直线电机在低速运行时，死区效应和电机参数变化会引起磁链漂移趋势增大，为了提高动子位置估算精确度，需要消除这些引起磁链变化趋势增大的不利因素。

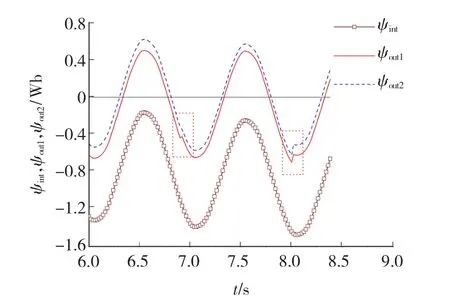
图3 磁链畸变Fig．3 Distortion of flux linkage

3．3 死区补偿

式(5)中的电机电压无法直接检测，一般采用直流母线电压和占空比对相电压进行重构，这种方法容易实现，但是他有一个不能忽略的问题，就是死区效应的影响。逆变器电路中为了有效防止三相全桥中同一桥臂的共通状态，需要在同一桥臂两个开关管的控制信号中加入死区，死区会使输出电压产生六次谐波，同时降低有效输出电压，电机低速运行时死区效应的影响更加明显。在反电势积分算法中，由于进行计算的电压与实际电压存在差异，使得磁链漂移问题更加严重。本文采用磁链中值法消除反电势积分引起的磁链漂移，假如上周期和本周期的磁链中值偏差过大，如图4(a)所示，在本周期使用上周期的磁链中值消除磁链漂移，误差就会增大。直线电机一般运行在低频状态下，死区效应更加明显，所以有必要采用死区补偿算法减少输出电压与计算时所使用电压的差异，减缓磁链漂移趋势，以提高动子位置的估算精确度。死区补偿方法为:根据死区时间确定死区误差电压矢量幅值，并在静止α－β坐标系下对死区误差电压矢量进行补偿［15］。由图4(a)可知，相邻两个运行周期磁链漂移趋势越来越大，加入死区补偿后，如图4(b)所示，磁链漂移趋势减缓，之后再利用磁链中值消除磁链漂移，可以有效降低动子位置估计误差。

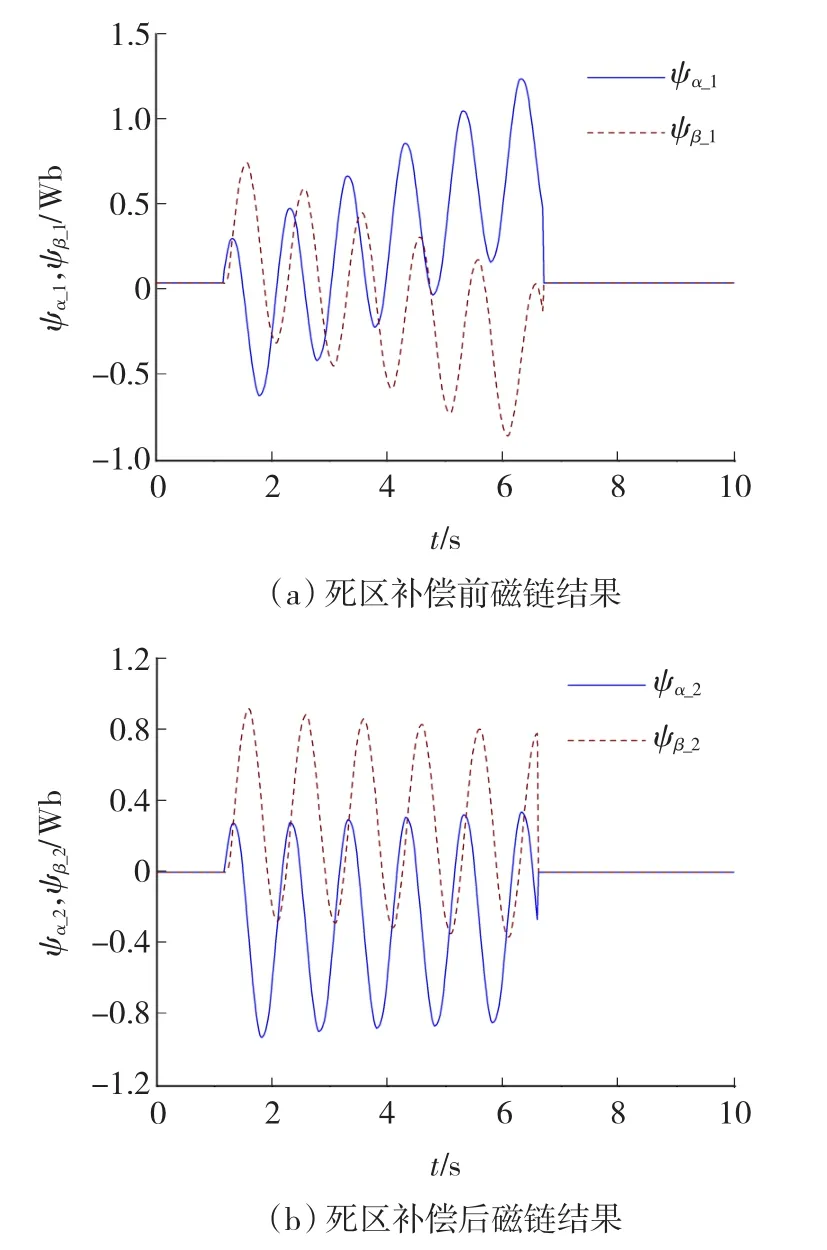
图4 死区补偿对磁链漂移的改善Fig．4 Rectification of flux linkage drift by dead time compensation

3．4 动子位置估算结果

通过反电势积分得到两相静止坐标系下的磁链分量，采用磁链中值法消除磁链零漂后，由式(6)即可得到动子位置，值域为［－π，π］。由双路线性霍尔传感器检测动子磁极位置并将其作为实际的动子位置。开环3 Hz运行时的动子位置估算实验结果如图5所示，图5中，θest为估算得到的动子位置，θr为实际检测到的动子位置，Δθ为估算误差。速度估算结果如图6所示。图6中，vhall为由霍尔传感器采集的速度，vest为速度估算值。

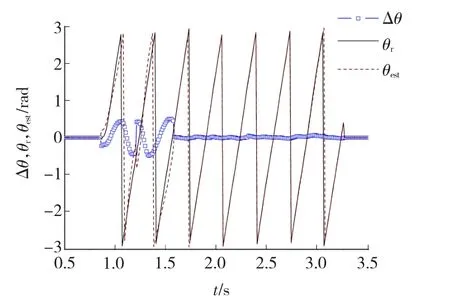
图5 动子位置估算结果Fig．5 Estimation results of mover position

图6 速度估算结果Fig．6 Estimation results of velocity

预测均方根误差eRMSEP可作为评判估算精确度的指标，其计算方法为

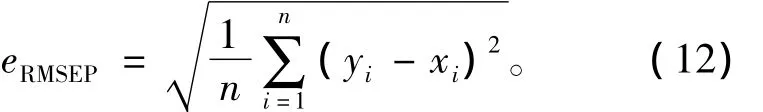
式中:yi为动子位置估算值;xi为动子位置测量值;n为统计样本数。eRMSEP越小说明动子位置估算精确度越高。

表1为直线电机在不同运行频率时动子位置估算结果的均方根误差。运行频率为1 Hz时均方根误差为0.072 6 rad，说明在低频时电机反电势很小，即使经过死区效应补偿并且采用无延时的磁链中值法消除磁链零漂，较小的反电势信号还是容易受到干扰。系统采样误差是干扰的主要来源，电流信号采样过程会在以下环节引入误差:电流传感器本身的精确度影响;信号输送到DSP的AD外设之前需要进行电平转换，多级运算放大器电路导致信号经过电平变化之后产生非线性失真;DSP的AD外设精确度影响。当运行频率超过3 Hz后，动子位置估算结果的均方根误差减小到0.024 0 rad，说明反电势增大对动子位置估算精确度有明显提高。

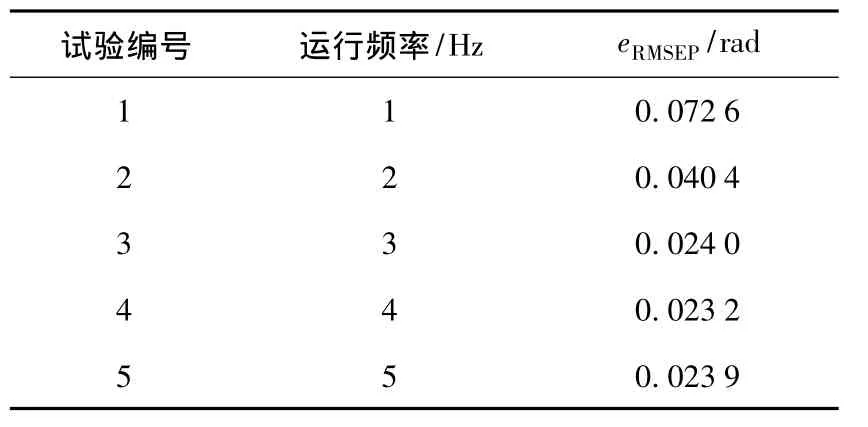
表1 不同运行频率下动子位置估算结果均方根误差Table 1 The eRMSEPof mover position in different operating frequencies

3．5 电机参数对动子位置估算精确度的影响

动子位置估算中用到的电机的参数有d、q轴电感和定子电枢电阻。在3 Hz运行频率下，将电感值增加50%，估算角度的预测均方根误差为0.030 2 rad，将电感值减小50%，估算角度的预测均方根误差为0.029 1 rad，误差变化均不明显。关于电感对动子位置估算的影响可以从式(4)中观察趋势，由于电机电感L1数值很小，在运行电流比较小时，式中iαL1和iβL1所占权重很小，对结果影响较小。

同样在3 Hz运行频率下，将电枢电阻增加10%，动子位置估算结果的均方根误差为0.033 7 rad，将电枢电阻减小10%，动子位置估算结果的均方根误差为0.033 6 rad，由此可知，电阻对动子位置估算结果的影响要强于电感。电阻值变化之后，磁链漂移趋势增大，如图7所示。采用两次磁链中值可以消除积分漂移，一定程度上可减少电枢电阻变化对动子位置估算精确度的影响。但是在这种情况下磁链的畸变会增加，如图3所示。受磁链畸变的影响，动子位置估算结果的误差还是会增大。

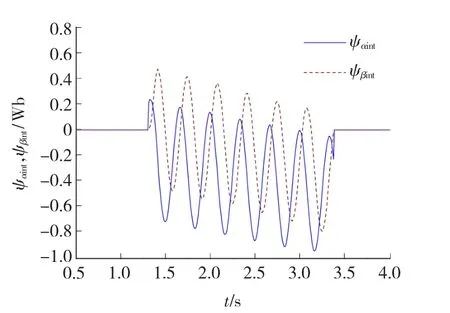
图7 电阻增加10%磁链变化Fig．7 Variation of flux linkage after resistance increased by 10%

4 结语

本文采用基于磁链变化的位置估算方法对永磁直线同步电机动子位置和速度进行估算，通过死区补偿策略消除死区效应带来的电压下降，解决了反电势纯积分造成的磁链漂移趋势过大的问题。并采用磁链中值法消除磁链漂移，这种方法计算量小且易于实现，同时避免了由滤波器带来的信号延迟问题。基于磁链变化的位置检测方法可以应用于长行程且不适合安装光栅等速度或位置传感器的直线电机控制系统中进行速度闭环矢量控制，如直线电机驱动的物流系统等。控制系统以电流闭环，速度开环方式启动，加速到较低频率就可使用估算得到的动子位置和速度进行速度闭环控制。基于磁链变化的位置检测方法依赖于准确的反电势信息，需要进一步完善采样及控制电路，选用较高精确度的电流传感器，使用独立的AD采样芯片，减少电流信号的调理过程，对电机参数进行更精确的测量等措施均可提高直线电机动子位置的辨识精确度。

［1］叶云岳．直线电机原理与应用［M］．北京:机械工业出版社，2000:1－28．

［2］刘晓，叶云岳，郑灼，等．一种低成本的线性霍尔位置检测方法研究［J］．浙江大学学报:工学版，2008，42(7):1204－1207．

LIU Xiao，YE Yunyue，ZHENG Zhuo，et al．Low-cost motor position detection method by linear Hall-effect sensors［J］．Journal of Zhejiang University:Engineering Science，2008，42(7):1204－1207．

［3］GENDUSO F，MICELI R，RANDO C，et al．Back EMF sensorless－ control algorithm for high-dynamic performance PMSM［J］．IEEE Transactions on Industrial Electronics，2010，57(6):2092－2100．

［4］周元钧，蔡名飞．改进的永磁同步电机转子初始位置检测方法［J］．电机与控制学报，2010，14(3):68－72．

ZHOU Yuanjun，CAI Mingfei．Initial rotor position inspection of PMSM based on rotating high frequency voltage signal injection［J］．Electric machines and Control，2010，14(3):68 －72．

［5］秦峰，贺益康，刘毅，等．两种高频信号注入法的无传感器运行研究［J］．中国电机工程学报，2005，25(5):116－121．

QIN Feng，HE Yikang，LIU Yi，et al．Comparative investigation of sensorless control with two high-frequency signal injection schemes［J］．Proceedings of the CSEE，2005，25(5):116－121．

［6］范蟠果，杨耕．感应电机无速度传感器控制自适应速度观测器［J］．电机与控制学报，2008，12(6):621－628．

FAN Panguo，YANG Geng．Adaptive speed observer for speed sensorless control of induction motor［J］．Electric machines and Control，2008，12(6):621 －628．

［7］陆华才，徐月同．基于AEKF的永磁直线同步电机速度和位置估计算法［J］．中国电机工程学报，2009，29(33):90－94．

LU Huacai，XU Yuetong．Speed and position estimation algorithm of permanent magnet linear synchronous motor based on augmented extended kalman filter［J］．Proceedings of the CSEE，2009，29(33):90－94．

［8］ACARNLEY P P，WATSON J．Review of position-sensorless operation of brushless permanent-magnet machines［J］．IEEE Transactions on Industrial Electronics，2006，53(2):352 －362．

［9］LEIDHOLD R，MUTSCHLER P．Speed sensorless control of a long-stator linear synchronous motor arranged in multiple segments［J］．IEEE Transactions on Industrial Electronics，2007，54(6):3246－3254．

［10］WANG Xiaoxin，GE Qiongxuan．Speed sensorless control of a linear synchronous motor using state observer on d-q reference frame［C］//International Conference on Electrical Machines and Systems，2008，ICEMS 2008，October 17－20，2008，Wuhan，China．2008:1553－1557．

［11］陆华才．无位置传感器永磁直线同步电机进给系统初始位置估计及控制研究［D］．杭州:浙江大学机械与能源工程学院，2008．

［12］唐任远．现代永磁电机理论与设计［M］．北京:机械工业出版社，1997:234－272．

［13］汤蕴璆，张奕黄，范瑜．交流电机动态分析［M］．北京:机械工业出版社，2004:91－172．

［14］WANG Chuanyang，XU L．A novel approach for sensorless control of PM machines down to zero speed without signal injection or special PWM technique［J］．IEEE Transactions on Power Electronics，2004，19(6):1601 －1607．

［15］WANG Li，YE Yunyue，LU Qinfen．Dead-time compensation in metro linear motor drive system［C］//2011 Chinese Control and Decision Conference，May 23 － 25，2011，Mianyang，China．2011:1230－1234．