新型横向磁通永磁电机无位置传感器控制

涂小涛，辜承林

(华中科技大学 强电磁工程与新技术国家重点实验室，湖北 武汉430074)

0 引言

横向磁通永磁电机(transverse－flux permanent magnet motors，TFPMM)克服了传统电机齿槽位于同一截面，几何尺寸相互制约，电机转矩难以根本提高的缺陷，成为电机领域的一个研究热点。近年来，新型拓扑结构、参数优化设计方面已取得阶段性成果，各类样机不断推出[1－6]。但控制方面的文献还较少，主要集中在永磁同步电机驱动模式，功率因数偏低的问题尚未得到有效解决[7]。而理论上，理想的无刷直流驱动模式有可能规避这一问题，同时节约驱动系统成本。为此，本课题组研制的三相新型TFPMM[3，8]，采用两两导通方式的无刷直流驱动模式。

有位置传感器技术在无刷直流电机(brushless DC motors，BLDCM)控制中最为成熟，但过于依赖位置信号，难以规避传感器件及连接线失效风险。相比之下，无位置控制技术勿需传感器，无连接线，消除了安全隐患，技术优势明显。无位置传感器控制方法很多，其中反电动势过零点检测技术最成熟、应用最广泛[9－10]，相关产品亦日趋完善，这也使得新型TFPMM无位置传感器控制应用成为可能。

从实用角度出发，新型TFPMM仍采用反电动势过零点检测中常用的相电压法，但附加检测误差的出现使其不能采用普通BLDCM的处理方法。本文结合新型TFPMM的无刷直流运行特点，探讨基于相电压法的无位置运行控制规律，从而奠定无位置运行控制应用的理论基础。

1 无刷直流运行特点

1.1 换流过程

对于理想BLDCM，常采用正常换相方式(滞后空载反电动势过零点30°换相)，假设三相反电动势在换相过程中保持不变，不考虑PWM控制的影响，忽略电阻压降，推导出关断相电流降为零的时间为

式中:Ls为定子自感;M为相间互感;Udc为直流母线电压;E为相反电动势幅值;I为方波电流幅值。

与普通BLDCM不同，新型 TFPMM(如图1所示)电感较大，且三相磁路解耦，不存在互感(即M=0)，加之低压大电流的应用要求(即Udc、E均较小，I较大)，结合式(1)可知，换流过程比较长。因此，采用普通BLDCM控制器(电压源型)时，电流并非理想方波，其轴线将沿着滞后反电动势方向偏移，且电流越大，偏移愈严重，性能影响也就愈明显[11]。

图1 新型横向磁通永磁电机定、转子三维结构Fig.1 Novel transverse-flux permanent magnet motor

1.2 电枢反应

新型TFPMM电枢磁链较大，对气隙磁场分布影响很大，电枢反应不可忽略。由于三相磁路解耦，只需分析一相的电枢反应情况。新型TFPMM导体不直接切割气隙磁场，而是通过感应气隙磁密变化产生反电动势。在电动机运行状态中，电枢磁场超前转子磁场，随着负载电流不断增大，电枢反应不断增强，导致气隙合成磁场波形逆转向畸变，负载反电动势随之向前畸变，最佳换相位置随之发生变化，从而影响电机运行性能[12]。

1.3 补偿措施

在有刷直流电动机中，大容量电机通过补偿绕组和换向极来削弱电枢反应和抵消电抗电动势，从而改善换向条件，而小容量电机一般采用逆转向移动电刷的做法，其本质在BLDCM中就相当于提前换相。有鉴于此，可通过采用提前换相方式，削弱新型TFPMM换流过程和电枢反应的不利影响，一定程度改善电流波形的同时，为二极管续流提供更为充足的空间，创造有利于电流与反电动势轴线重合(等效于Id=0)的环境，此时二者乘积最大，即转矩电流比最大[13]，并认为电机为最佳运行，对应的提前换相角(相对空载反电动势整定)也为最佳。

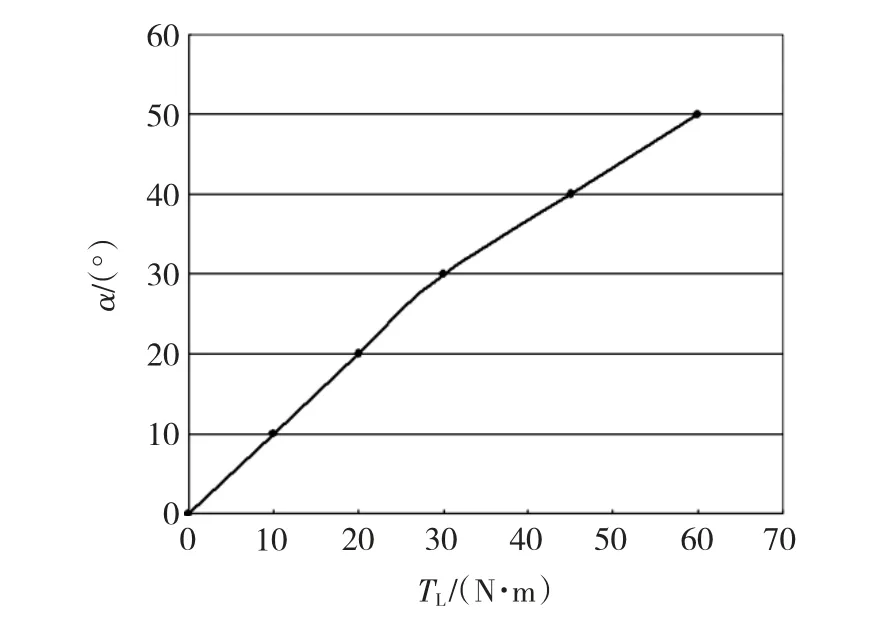
图2 最佳提前换相角与负载转矩的关系曲线Fig.2 Relation curve between optimal phase advance angle and load torque

实际上，最佳提前换相角 α随负载转矩 TL变化，二者间的实测关系曲线如图2所示。图3为有位置传感器时不同提前换相角下的性能对比情况。结果表明，实时适当提前换相，确能有效改善电机性能，机械特性变硬，效率和负载能力明显提升。

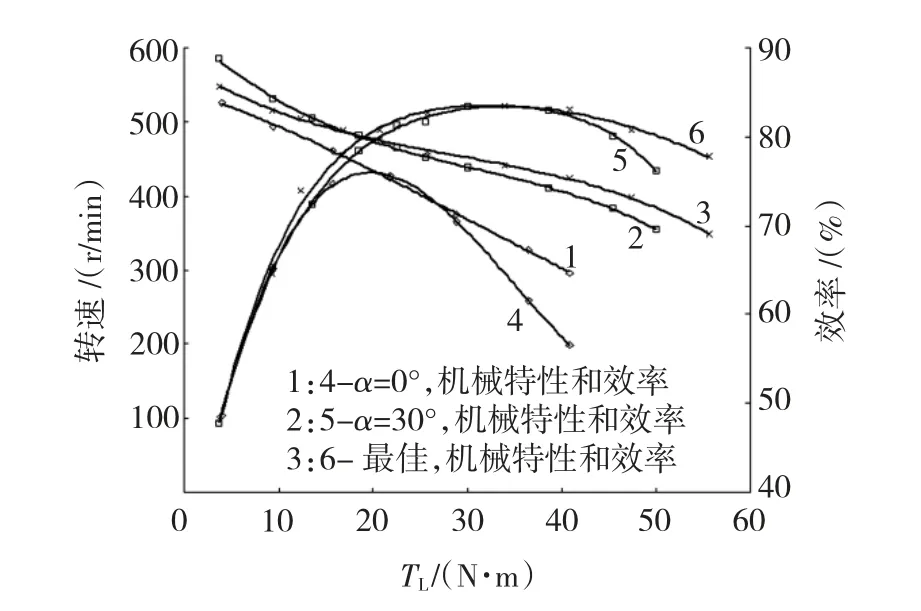
图3 不同提前导通角时性能对比Fig.3 Results with different phase advance angles

2 无位置传感器控制方式

2.1 相电压法检测误差产生机理

采用反电动势过零点检测中常用的相电压法，相应的检测电路如图4所示。根据对称性原理，当反电动势过零点时，O点电压与绕组中性点电压相等，此时相电压过零点即为反电动势过零点。为消除PWM斩波等高频电磁干扰，实际应用中需对相电压进行滤波处理，并可通过加大滤波深度有效消除二极管续流产生的电压尖峰对反电动势过零点检测的干扰，保证滤波后相电压在每个60°区间内只有一个过零点。

图4 相电压法检测电路示意图Fig.4 Schematic diagram of phase-voltage method

对于普通BLDCM，认为滤波前后相电压与反电动势过零点始终重合，因此可直接由滤波电路参数计算出滤波相移，并加以适当的相位修正，从而获得较为准确的换相时刻。但此处理方法直接应用于新型TFPMM并不可行，具体分析如下。

方便起见，不妨先忽略电枢反应的影响，并假设反电动势波形为正弦，PWM占空比为1(即认为无高频干扰)。以从图4中开关管T5、T6导通切换至T1、T6导通为例，取换相开始时刻为时间零点，设C相电流下降过程为0～θf，可推导出该60°区间内三相电压方程，并以A相为例，即

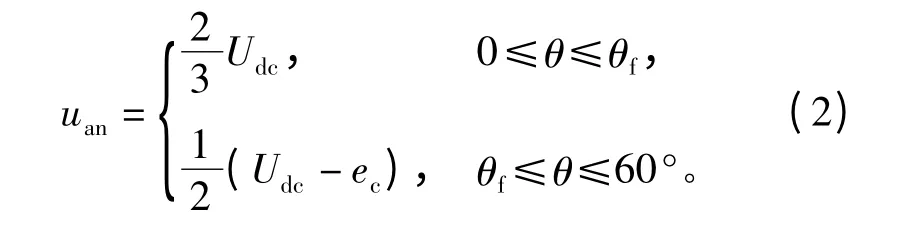
式中:ec为C相反电动势。

同理，可推导出 A相电压其他区间内的表达式，在此不再一一列出。

由相电压方程绘制出其相应波形，并给出对应反电动势波形，如图5中上半部分所示，其中相电压的尖峰部分(如0～θf对应部分)是由换流过程中二极管续流所致。

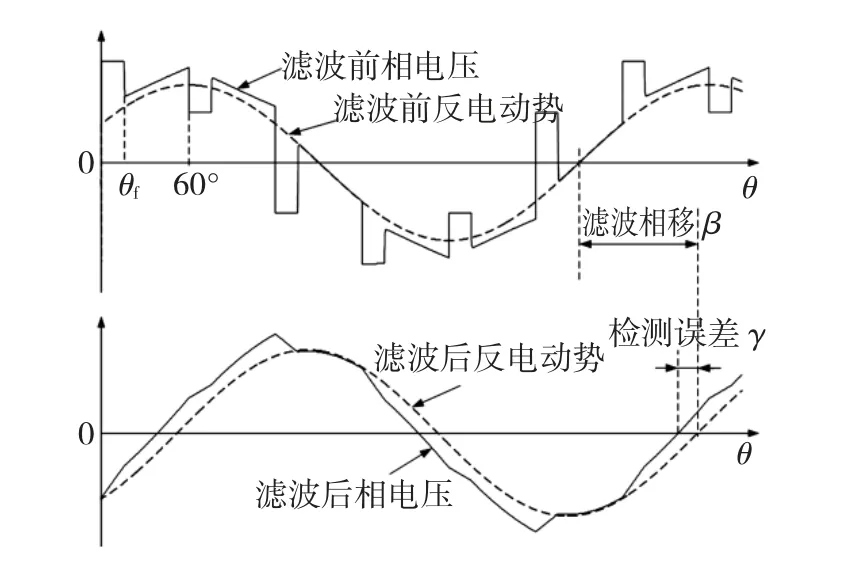
图5 滤波前后相电压与反电动势过零点关系Fig.5 Zero crossing points of phase voltage and back EMF without and with low filter

特别地，有两种极端情况需要分别讨论。一种情况是，当θf→0时，相电压与反电动势轴线重合，如图6(a)所示，此时可认为滤波后二者过零点仍重合，这也正是普通BLDCM所出现的情况。另一种情况是，假设θf→60°时，相电压与反电动势轴线出现明显相位差，如图6(b)所示，与前一种情况的波形对比表明，换流引起的相电压尖峰部分会导致相电压向前畸变，其基波相位也将超前反电动势。

所以，针对相电压法起作用的情况(即反电动势过零点处于悬空状态)，由于新型TFPMM换流过程较长，当相电压尖峰宽度增大至一定时，经低通滤波器后，相电压过零点明显超前反电动势过零点，如图5所示，二者间的相位差定义为常规相电压法引入的附加检测误差，记为 γ，且相电压尖峰宽度越大，γ越大。

进一步地，换流过程长短决定相电压尖峰宽度。只讨论基于最大转矩电流比的调压调速过程，电机外施电压与转速近似成正比，结合式(1)进一步推导出换流过程持续电角度为

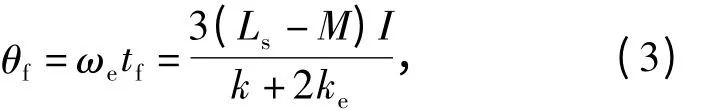
式中:ωe为电角速度;ke为反电动势系数;k近似为常数，且 k ≈ Udc/ωe。

图6 两种极端情况下相电压与反电动势波形Fig.6 Waveforms of phase voltage and EMF at two extremes

由此可见，调速过程中转速对换流过程的影响可忽略，换流过程主要受负载大小影响，即负载转矩(或电枢电流)越大，换流过程越长。相应地，相电压尖峰也就越宽，附加检测误差γ也就增大。

显然，即使实际存在电枢反应和 PWM斩波等高频干扰，上述分析结果依然有效。不过，此时附加检测误差γ应为滤波后相电压过零点超前滤波后负载反电动势过零点的相位。

若仿普通 BLDCM，在新型 TFPMM中，仍认为滤波前后相电压与反电动势过零点始终重合，最终获得的换相时刻将超前实际所需换相时刻，从而降低电机运行性能[14]，严重时还会导致电机失步。因此，必须对附加检测误差作相应相位补偿。

2.2 补偿策略

鉴于新型TFPMM电枢反应比较强烈，负载反电动势波形会严重畸变，通过解析方法计算附加检测误差γ将十分繁杂，工程应用价值也不大。

相比而言，通过实验测定附加检测误差与负载间的定量关系，并用查表法加以实现的方法更为有效、实用。考虑到有、无位置传感器控制方式只是获取转子位置信息的方式不同，可以通过有位置实验测定最佳运行状况下不同负载对应的附加检测误差γ。实际上，受电枢反应的影响，负载反电动势过零点位置会随负载变化而移动，无法直接测定附加检测误差γ。但是，实验中可以测定滤波后相电压过零点与滤波后空载反电动势过零点间的相位差，记为γ0。这是因为在新型TFPMM中位置传感器输出信号为转子物理位置(不随负载变化)，可有效反映空载反电动势过零点位置，于是滤波后空载反电动势过零点位置可由滤波相移估算出来。滤波相移计算为

式中:f为反电动势频率。

显然，γ0与γ间的差值为滤波后负载反电动势过零点超前滤波后空载反电动势过零点的相位，由电枢反应引起。此时，对附加检测误差γ的补偿已转化成对γ0的补偿，并且理论上可通过对γ0的补偿正确估算出空载反电动势过零点位置。

为避免出现检测到某相电压过零点时已经错过该相换相的情况，可借鉴普通BLDCM中90°－β无位置控制方案，检测到 A相滤波后相电压过零点时，经过适当相位补偿后获得B相换相时刻，如图7所示。图示结果表明，由图中3位置延迟120°－β+γ0电角度可估算出7位置，而图2给出的最佳提前换相角α正是相对空载反电动势而测定的，由7位置再延迟30°－α电角度即可确定8位置。因此，实际检测到A相滤波后相电压过零点时，延迟150°－β+γ0－α电角度后即为B相换相时刻，其他换相时刻可同理推出。

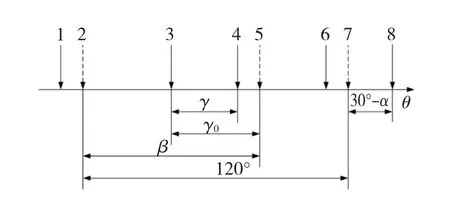
图7 相位补偿示意图Fig.7 Schematic diagram of phase compensation

3 实验与讨论

针对相电压法应用于新型TFPMM会引入附加检测误差的问题，以dSPACE为处理核心，搭建无位置传感器控制系统。新型TFPMM样机参数见表1。相电压检测电路设计参数为:R1=R3=R5=47 kΩ，R2=R4=R6=10 kΩ，C1=C2=C3=2.2 μF。电机起动借助Hall位置传感器，起动成功后，切换至无位置传感器工作方式运行。

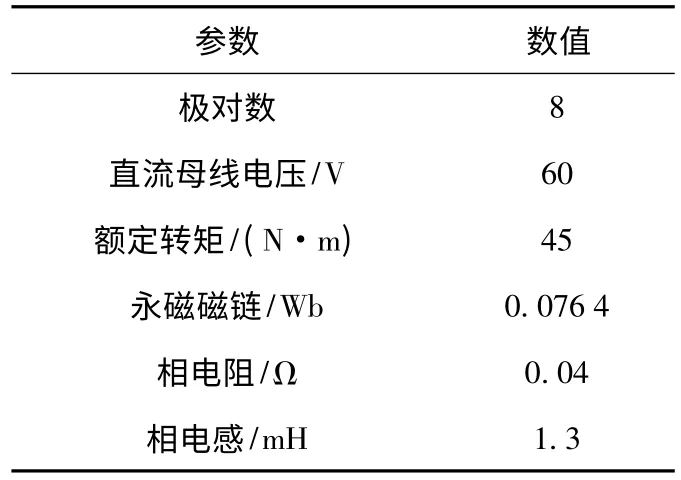
表1 样机参数Table 1 Parameters of the prototype

发电机空载时，通过外加Hall位置传感器锁定某转速下滤波后空载反电动势相位，而后利用有位置控制器控制电机以该转速运行，实测滤波后相电压与空载反电动势相位关系如图8所示，前者明显超前后者，且随负载转矩增大而增大，与理论分析吻合。图9为实测最佳运行时γ0与负载转矩间的拟合关系曲线，用作无位置相位补偿依据。

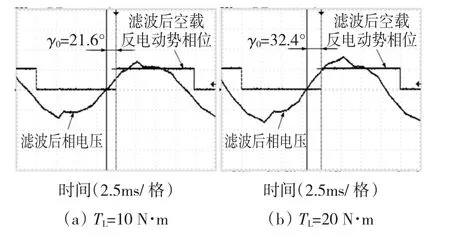
图8 实测滤波后相电压与反电动势相位关系Fig.8 Measured phase relation between phase voltage and back EMF after being filtered

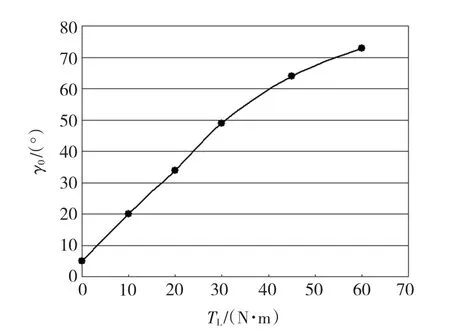
图9 实测检测误差与负载转矩间的关系曲线Fig.9 Measured relation curve between detection error and load torque

新型TFPMM在自制实验装置下作无位置运行时，对检测误差作相位补偿前、后的实验结果分别如图10和图11所示，其中Hall信号与相电流对应的空载反电动势同相位，二者相位关系清楚显示了提前换相角大小，已在图中标明。特别说明，图11中电机转速明显高于图10，电机内部损耗更大，且轻载时其比重较大，相同负载转矩对应的电磁转矩也更大，故出现轻载时图11中电流反而更大的情况，但不影响以下实验结果分析。

若不作相位补偿，由图10结果可知，当 TL=5 N·m时，检测误差比较小，其影响还不够明显;但增至TL=10 N·m时，换相时刻明显超前最佳位置(参见图2)，电机处于过提前换相状态，这正是前述检测误差所致，与理论分析相吻合;检测误差还会随负载转矩增加而进一步增大，实验过程中继续稍微增加负载转矩即出现电机失步现象。而相比之下，作相位补偿后，图11结果显示，在负载转矩逐渐增大的过程中，电机换相时刻与图2结果基本一致，且负载能力显著增强，可在额定负载附近运行。

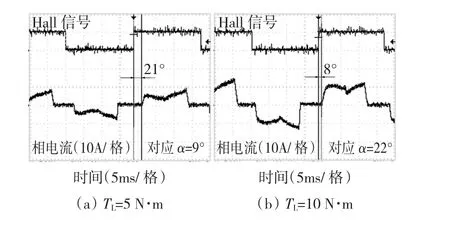
图10 相位补偿前的实验结果Fig.10 Measured results without phase compensation

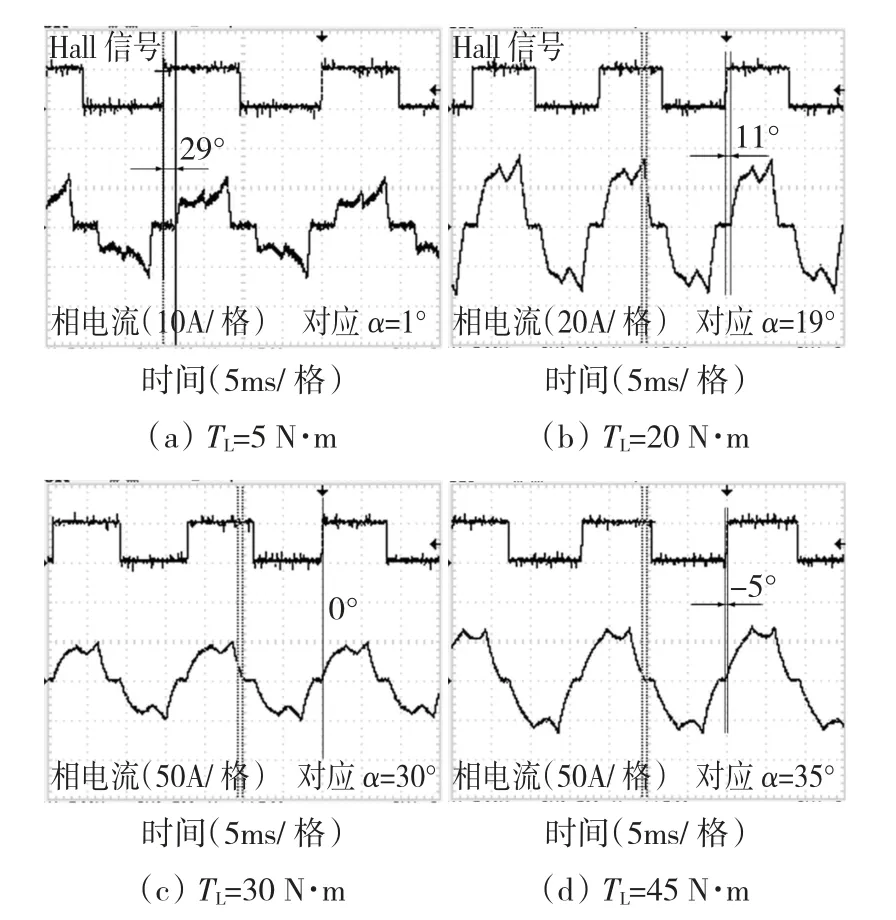
图11 相位补偿后的实验结果Fig.11 Measured results with phase compensation

进一步地，测定对检测误差作相位补偿后电机机械特性和效率曲线，并与有位置运行结果对比，如图12所示。可以看出，常规相电压法的改进方案可使新型TFPMM获得较好的无位置运行性能。但随着负载转矩继续增大，反电动势过零点容易因二极管续流而被淹没，相电压法失效，电机会出现失步。

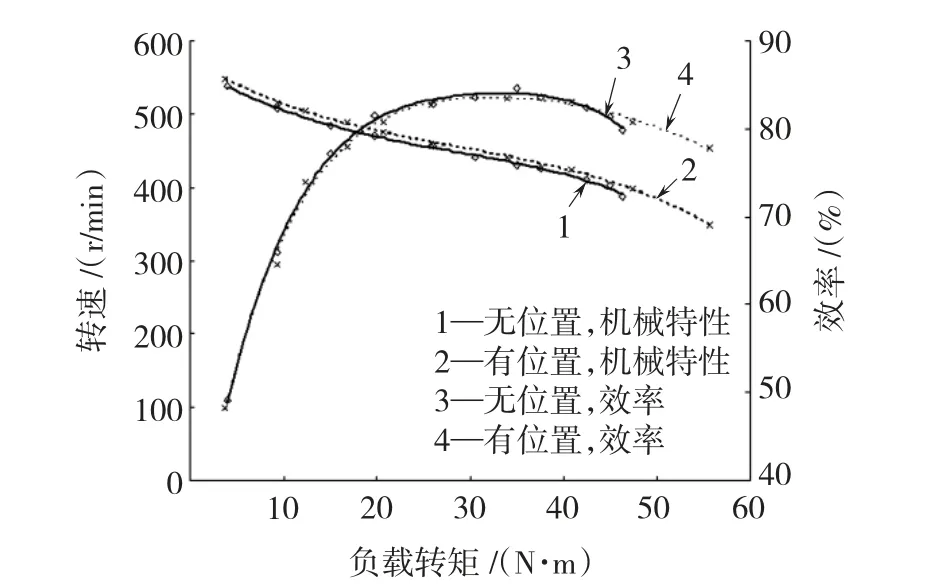
图12 检测误差补偿后无位置运行结果Fig.12 Experimental results of sensorless control with proposed scheme

4 结语

常规相电压法应用于新型TFPMM时会引入附加检测误差，必须加以修正，并由此提出了相应的补偿方案，获得了较为满意的运行性能。该方案只需在控制芯片中通过软件编程实现，硬件构造与常规BLDCM无位置控制器相同，具有较强的实用性。

但实验发现，该方法在重载或过载时仍存在失效风险。为此，还需要进一步探索更为可靠的应对措施，相关研究进展待后续发表。

[1]MASMOUDI A，NJEH A，MANSOURI A，et al.Optimizing the overlap between the stator teeth of a claw pole transverse-flux permanent-magnet machine[J].IEEE Transactions on Magnetics，2004，3(3):1573 －1578.

[2]郑文鹏，江建中，李永斌.基于三维磁网络法E型铁心横向磁场电机的设计与研究[J].中国电机工程学报，2004，24(8):138－141.ZHENG Wenpeng，JIANG Jianzhong，LI Yongbin.Design and analysis on tranverse flux machine with E-shaped stator cores based on 3D magnetic network method[J].Proceedings of the CSEE，2004，24(8):138－141.

[3]陈金涛，辜承林.新型横向磁通永磁电机研究[J].中国电机工程学报，2005，25(15):155 －160.CHEN Jintao，GU Chenglin.Study on novel transverse-flux permanent magnet machine[J].Proceedings of the CSEE，2005，25(15):155－160.

[4]刘哲民，陈谢杰，陈丽香，等.基于3D－FEM的新型横向磁通永磁电机的研究[J].电工技术学报，2006，21(5):19 －23.LIU Zhemin，CHEN Xiejie，CHEN Lixiang，et al.Study of a new transverse flux permanent magnet machine based on 3D-FEM[J].Transactions of China Electrotechnical Society，2006，21(5):19－23.

[5]LI Wenlong，CHAU K T.Design and analysis of a novel linear transverse flux permanent magnet motor using HTS magnetic shielding[J].IEEE Transactions on Applied Superconductivity，2010，20(3):1106－1109.

[6]王骞，邹继斌，赵玫.横向磁场永磁直线电机结构及电感参数分析[J].电机与控制学报，2010，14(11):155 －160.WANG Qian，ZOU Jibin，ZHAO Mei.Analysis of structure and inductance on a transverse flux permanent magnet Linear Machine[J].Electric Machines and Control，2010，14(11):155 － 160.

[7]MASMOUDI A.On the Attempts to optimize the performance and cost-effectiveness of TFPM drives:a crucial challenge for the automotive industry[J].European Transactions on Electrical Power，2005，15(6):481 －495.

[8]褚文强，辜承林.新型横向磁通永磁电机磁场研究[J].中国电机工程学报，2007，27(24):58 －62.CHU Wenqiang，GU Chenglin.Study on magnet field of novel transverse-flux permanent magnet machine[J].Proceedings of the CSEE，2007，27(24):58 －62.

[9]李自成，程善美，秦忆.线反电动势检测无刷直流电机转子位置方法[J].电机与控制学报，2010，14(12):96 －100.LI Zicheng，CHENG Shanmei，QIN Yi.Novel rotor position detection method of line back EMF for BLDCM[J].Electric Machines and Control，2010，14(12):96 －100.

[10]CHEN Chenghu，CHENG Mingyang.A new cost effective sensorless commutation method for brushless DC motors without phase shift circuit and neutral voltage[J].IEEE Transactions on Power Electronics，2007，22(2):644 －653.

[11]王晋，陶桂林，周理兵，等.基于换相过程分析的无刷直流电动机机械特性的研究[J].中国电机工程学报，2005，25(14):141－145.WANG Jin，TAO Guilin，ZHOU Libing，et al.Research on the mechanical characteristic of brushless DC motors based on the analysis of phase commutation[J].Proceedings of the CSEE，2005，25(14):141 －145.

[12]刘明基，姚郁，邹继斌，等.无刷电机中电枢反应对换向电动势相位的影响[J].微电机，2001，(4):3 －5.LIU Mingji，YAO Yu，ZOU Jibin，et al.Effect of the armature reaction on the phase of the commutation E.M.F.in brushless DC motors[J].Micromotors，2001，(4):3 － 5.

[13]罗宏浩，吴峻，赵宏涛，等.永磁无刷直流电机换相控制研究[J].中国电机工程学报，2008，28(24):108 －112.LUO Honghao，WU Jun，ZHAO Hongtao，et al.Commutation control of permanent brushless DC motors[J].Proceedings of the CSEE，2008，28(24):108 －112.

[14]胡勤丰，严仰光.永磁式双凸极电机角度提前控制方式[J].电工技术学报，2005，20(9):13 －18.HU Qinfeng，YAN Yangguang.Prior angle control for doubly salient permanent magnet motor[J].Transactions of China Electrotechnical Society，2005，20(9):13 － 18.