一种微型燃气轮机抗扰控制器设计及验证方法

段建东，孙力，赵克，吴凤江，王要强

(哈尔滨工业大学 电气工程系，黑龙江 哈尔滨150001)

0 引言

微燃机具有功率密度大、高效率、低排放等特点，近年来得到迅速发展，国内外学者在这一领域进行了卓有成效的研究[1－3]。微燃机控制器是决定系统性能的主要部件之一，在产品的研制阶段直接利用实际系统调试会造成局部过热、转子变形等损害甚至发生火灾、飞车等重大事故，因此有必要研究微燃机的动态模拟系统，用于控制器的设计和性能验证。

由于研究目的不同，文献中微燃机数学模型复杂程度存在较大差异。较复杂的模型是考虑部分工况的非线性模型，用于研究微燃机的机械特性和热力学特性[4－6]，对于控制器设计使用较多的是额定工况下的小扰动模型[7－10]。本文在 Rowen模型基础上建立了微燃机稳态工作点处小扰动模型。经分析发现变频器驱动异步电机调速系统具有与微燃机近似的动态模型。基于动态模型相似性对异步电机调速系统进行调整使其与微燃机控制系统具有相同的模型结构。因此可以利用微燃机模拟系统进行控制器设计和性能验证，无疑这种方案既安全又可以在短时间内重复试验[11－14]。

此外由于实际系统轴系的转动惯量较大，负载扰动导致转速的变化需要较长时间，显然基于转速误差的调节器输出会明显滞后，因此，造成系统动态调节时间长、转速波动大、抗负载扰动能力差等问题。本文提出的负载前馈控制基于模型分析找到了解决办法，使负载的变化直接影响燃料的大小，缩短了调节时间、增强了抗负载扰动的能力。利用Matlab进行了仿真，最后在模拟系统实验平台上进行了验证。

1 微型燃气轮机动态模型

系统的启动和停机是转速开环控制，在稳态工作点附近切入转速闭环调节，因此建立的动态模型适用于稳态工作点附近而不包括系统启停的大动态过程。假设稳态下空气流量不变，温度环不起作用，暂不考虑负载扰动，则系统动态模型框图如图1所示。其中Gω(s)是速度调节器传函;燃料伺服系统近似为一阶惯性环节，时间常数为τf;燃烧室为纯滞后延时环节，时间常数为 τB;压气机等效为具有增益的一阶惯性环节，Kk为增益系数，τk为时间常数;透平的输出转矩为TT(s)=f1(s)=K1W'f(s)+K2ω(s)，K1为与燃料相关系数，K2为与转速相关系数，W'f(s)为透平等效燃料输入;TL(s)是负载转矩;轴系为积分环节，Jr为轴系的转动惯量[15－18]。

在稳态工作点附近令TL(s)=0，则可求出透平等效燃料输入W'f(s)和转子角频率ω(s)之间的传递函数为

燃料伺服系统和压气机小惯性环节可以用一个惯性环节来等效，则系统开环传递函数可表示为

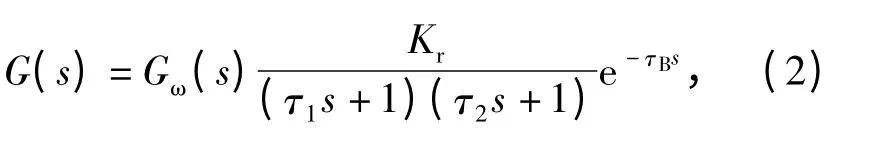
式中:Kr=K1Kk/K2为被控对象总增益;τ1=τf+τk为燃料伺服系统和压气机的总惯性时间常数;τ2=Jr/K2为透平轴系的惯性时间常数;τB为燃烧室纯滞后延时时间常数。

图1 微燃机动态结构Fig.1 Dynamic structure of micro-turbine

2 模拟系统动态模型及控制律设计

2.1 模拟系统动态模型

在模拟系统中用异步电机模拟微燃机透平，用变频器模拟压气机和燃料伺服系统的惯性环节，用数字延时环节代替燃烧室。设定系统的稳态工作点为2 000 r/min，转速调节器输出经限幅环节和D/A转换后变为模拟信号，作为变频器的输入。模拟系统的动态模型结构如图2所示，其中:Gn(s)为速度调节器传函;KDA为DA转换的比例系数;Kh为变频器中模拟信号输入对应频率给定的比例系数;τh为变频器近似一阶惯性环节的时间常数;Te为电机电磁转矩;TL为负载转矩;Jm为转子转动惯量;α为转速反馈系数。

图2 模拟系统动态结构Fig.2 Dynamic structure of the simulation system

异步电动机恒压频比正弦波供电时，当转差很小时忽略电动机的电磁惯性，电动机的机械特性方程式为

式中:np为电机极对数;Us为电机定子相电压有效值;ω1为电机同步角频率;ω为电机转子角频率;R'r为折合到定子侧的转子每相电阻。由于采用VVVF变频方式，所以设Ks=Us/ω1为常数。

令TL(s)=0，可求出 ω1(s)和 ω(s)的传递函数为

式中，τm=JmR'r/(3npKs2)。进而可求出模拟系统开环传函为

对比式(2)和式(5)发现模拟系统模型比微燃机模型少了一个延时环节，为了让模拟系统与微燃机模型具有相同的形式，在模拟系统中串入一个数字纯延时环节来模拟燃烧室，τZ为纯延时时间常数，修改后的模拟系统开环传函为

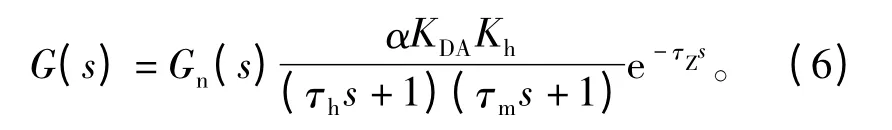
这样所建立的模拟系统模型与微燃机系统具有相同的开环传递函数结构。因此针对模拟系统模型进行控制器设计等效于对微燃机控制器规律的设计。

式(6)中具有指数函数 e－τZs，此系统为非最小相位系统，给控制器设计带来了不便，由于 τZ为大约10 ms的常数，对于这样小的纯延时环节可以近似为一阶惯性环节，则开环传函变为

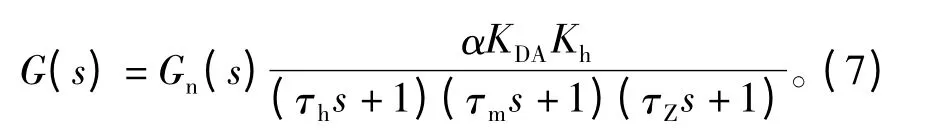
2.2 控制规律设计

所采用的微燃机模拟系统模型参数为DA转换增益KDA=0.003 9，变频器增益Kh=3.75，变频器惯性时间常数τh=1 s，纯延时时间常数 τZ=0.01 s轴系转动惯量Jm=0.001 5 kg·m2，折合到定子侧的转子每相电阻 R'r=0.151 Ω，异步电机额定相电压UsN=220 V，异步电机额定同步角频率ω1N=314 rad/s，电机惯性时间常数τm=0.026 s，转速反馈系数α=9.55，其中变频器惯性时间常数最大，异步电机和纯延时时间常数较小，系统的开环增益较小。

从被控对象的Bode图(图3)发现相角裕度和增益裕度都不满足系统稳定条件，且动态快速性和稳态精度差。不能满足微燃机系统稳态运行时具有良好平稳性、稳态精度、抗干扰能力以及不希望出现大转速超调的要求。针对被控对象的特点和系统对控制器的要求模拟系统采用PI控制。基于模拟系统得到的校正流程和参数整定经验可以应用于微燃机系统。

图3 模拟系统Bode图Fig.3 The Bode diagrams of the simulation system

PI控制的传递函数为

式中，Kpi为比例放大系数，τ1为微分项超前时间常数，τ1/Kpi为积分时间常数。从式(7)可知被控对象是由一个较大的惯性环节和两个较小的惯性环节组成的三惯性系统。将两个小惯性环节合并为一个，控制器微分项抵消大惯性环节，系统设计成典型Ⅰ型系统;或者将大惯性环节近似为积分环节，合并两个小惯性环节，系统设计成典型Ⅱ型系统。每种系统选择了两组参数，具体数值见表1，Bode图如图3所示。

表1 控制参数设计Table 2 Designing control parameters

由表1和图3可知，设计成典型Ⅰ型系统的特点是超调小、稳定裕度大和动态响应慢;设计成典型Ⅱ型系统的特点是超调较大、稳定裕度较小和动态响应快。

3 负载前馈控制

由于微燃机的转动惯量较大，负载发生变化需要较长时间反应到转速，并且PI调节器的输出还要经过延时和惯性环节才能反应到透平转矩，因此PI调节器不能很好的抑制负载扰动。转速调节器为PI控制无负载前馈时负载与转速的传函为

式中，Kn=αKDAKhKω。

加入负载前馈后的系统控制框图如图4所示，GL(s)为负载前馈通道的传函。有负载前馈的负载与转速的传函为

为了抵消大惯性的影响，令

式(10)变为

图4 模拟系统负载前馈控制框图Fig.4 Load feedforward control diagram of the simulation system

对比式(9)和式(12)可知加入负载前馈后传函的分子由纯微分和一阶微分环节变为二阶纯微分环节，减小了负载对转速动态影响而且可以抑制加速度输入的负载对转速的影响，增强了系统的抗负载扰动能力。

负载前馈控制的加入使燃油量不仅决定于调节器的输出而且还受负载的控制，负载的变化直接影响了燃油量，提高了系统对负载的动态特性。在模拟系统中证明了负载前馈控制的有效性。

4 仿真分析及实验验证

根据前文建立的微燃机和模拟系统动态模型，利用所设计的转速控制规律和负载前馈控制分析，在Matlab/SIMULINK中进行了仿真。图5(a)是按照典型Ⅰ型系统设计的两组调节器参数结果，随着比例增益的增大超调增大、调节时间减小、震荡次数增加。图5(b)是按典型Ⅱ型系统设计的两组调节器参数结果，比例增益对动态性能的影响与典型Ⅰ型系统相似。对比5(a)和图5(b)可知按典型Ⅰ型系统设计比Ⅱ型系统的超调小甚至无超调、震荡次数少、动态响应慢。仿真结果与前面的理论设计动态特性具有很好的一致性。图5(c)和图5(d)分别是Ⅰ型系统和Ⅱ型系统采用两组控制规律时突加负载有无负载前馈的仿真结果。由于负载前馈的引入加快了负载扰动时的转速恢复时间，减小了转速降，提高了系统的抗负载扰动性能，与前面的理论分析结果是一致的。

图5 仿真波形Fig.5 Simulation waveforms

基于前述理论分析设计和仿真验证构建了微燃机模拟系统实验平台，如图6所示。异步电机、直流启动发电机和步进电机同轴连接，直流启动发电机在启动过程用于拖动系统升速，利用步进电机端电压的过零点测取转速，同时步进电机作为负载元件。这样构建的实验平台可以模拟微燃机冷运转、启动、空载运行、带载运行、负载突变、故障模拟等工况。

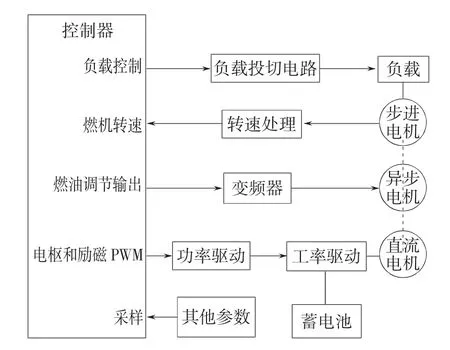
图6 模拟系统平台示意图Fig.6 The simulation system schematic diagram

控制器参数为Kpi=4.97、τ1=0.1，转速参考值由2 100 r/min变为1 900 r/min和由1 900 r/min变为2 100 r/min的实验结果如图7(a)、(b)所示，稳态误差为20 r/min，转速变化与前面的仿真一致，验证了理论分析设计的正确性。接入三相对称电阻的步进电机绕组电流反映了切入负载的变化和大小，没有负载前馈控制的实验结果如图7(c)所示，有负载前馈控制的实验结果如图7(d)所示。对比可知负载前馈控制的加入加快了转速闭环的动态过程，增强了抗负载扰动的能力，与前面的理论分析吻合。

图7 模拟系统实验波形Fig.7 The simulation system experimental waveforms

5 结语

基于动态模型的相似性增加了数字纯延时环节的变频器驱动异步电机调速系统构成了微燃机模拟系统。按照典型Ⅰ型系统设计的控制规律很好的满足了实际系统对平稳性、稳态精度及转速超调的要求。进一步在理论上分析了转速抗负载扰动动态性能差的原因，提出的负载前馈控制使负载与转速传函的分子由原来的纯微分、一阶微分环节变为二阶纯微分环节，加快了转速控制器对负载扰动的动态响应。Matlab仿真和模拟系统平台实验结果证明利用模拟系统调试控制器是正确而有效的，所提负载前馈控制的确增强了控制器抗负载扰动性。本文所提方法对微燃机控制器的研制具有理论参考价值和应用价值。

[1]赵克，耿加民，孙力.微型燃气轮机发电系统新型并网控制技术[J].电机与控制学报，2008，12(4):409 －414.ZHAO Ke，GENG Jiamin，SUN Li.Novel grid-connected control tecnniques for the microturbine generation system[J].Electric Machines and Control，2008，12(4):409 －414.

[2]耿加民，张化光，张宏杰.微型燃气轮机双向电力变换系统设计与研究[J].电机与控制学报，2007，11(5):551 －554.GENG Jiamin，ZHANG huaguang，ZHANG Hongjie.Design and research of bidirectional electric converter for micro － turbine[J].Electric Machines and Control，2007，11(5):551 －554.

[3]DAVIS M W，GIFFORD A H，KRUPA T J.Microturbines-an economic and reliability evaluation for commercial，residential，and remote load applications[J].IEEE Transactions on Power Systems，1999，14(4):1556 －1562.

[4]徐钢，林汝谋，邵艳军，等.燃气轮机建模的通用性和精细性研究[J].中国电机工程学报，2005，25(21):106 －111.XU Gang，LIN Rumou，SHAO Yanjun，et al.Study on universality and precision of gas turbine modeling[J].Proceedings of the CSEE，2005，25(21):106 －111.

[5]张化光，邓玮，耿加民.发电用燃气轮机的非线性数学建模及稳定性分析[J].中国电机工程学报，2007，27(26):108 －114.ZHANG Huaguang，DENG Wei，GENG Jiamin.Nonlinear modeling and stability analysis of gas turbine used for electricity generating[J].Proceedings of the CSEE，2007，27(26):108 －114.

[6]KUNITOMI K，KURITA A，OKAMOTO H.Modeling frequency dependency of gas turbine output[C]//IEEE Conference on Power Engineering，Columbus，2001.

[7]ROWEN W I.Simplified mathematical representations of heavy-duty gas turbines[J].American Society of Mechanical Engineers Journal of Engineering for Power，1983，105:865 －869.

[8]Working Group on Prime Mover and Energy Supply Models.Dynamic models for combined cycle plants in power system studies[J].IEEE Transactions on Power Systems，1994，9(3):1698－1708.

[9]Working Group on Prime Mover and Energy Supply Models.Hydraulic turbine and turbine control models for system dynamic studies[J].IEEE Transactions on Power Systems，1992，7(1):167－179.

[10]GUDA S R，WANG C，NEHRIR M H.A simulink-based microturbine model for distributed generation studies[C]//IEEE Proceedings of the Thirty-Seventh Annual North American Power Symposium，Ames，2005.

[11]张会生，刘永文，苏明，等.燃气轮机调速系统半物理仿真研究[J].系统仿真学报，2002，14(3):400 －402.ZHANG Huisheng，LIU Yongwen，SU Ming，et al.Hardware-inthe-loop simulation of the speed regulator of gas turbine[J].Journal of System Simulation，2002，14(3):400 － 402.

[12]程涛.小型涡喷发动机数控调节器的半实物仿真[J].航空动力学报，2004，19(3):383 －386.CHENG Tao.Hardware in the loop simulation of minitype turbojet engine digital control regulator[J].Journal of Aerospace Power，2004，19(3):383 －386.

[13]NITAIGOUR P M，KISEON K.A prototype for hardware-in-theloop simulationof a distributed control architecture[J].IEEE Transactions on Systems，Man，and Cybernetics:Part C:Applications and Reviews，2008，38(2):189 －200.

[14]GUILLAUD X，DEGOBERT Ph，LORIOL D.Real-time simulation of a micro-turbine integrated in a distribution network[C]//IEEE International Symposium on Power Electronics，Electrical Drives，Automation and Motion，Taormina，2006.

[15]SOON K Y，HUGHES F M，MILANOVIC J V.Comparative analysis and reconciliation of gas turbine models for stability studies[J].IEEE Power Engineering Society General Meeting，Tampa，2007.

[16]SAHA A K，CHOWDHURY S，CHOWDHURY S P，et al.Modeling and performance analysis of a microturbine as a distributed energy resource[J].IEEE Transactions on Energy Conversion，2009，24(2):529 －538.

[17]ROWEN W I.Simplified mathematical representations of single shaft gas turbines in mechanical drive service[C]//International Gas Turbine and Aeroengine Congress and Exposition，Cologne，1992.

[18]CENTENO P，EGIDO I，DOMINGO C，et al.Review of gas turbine models for power system stability studies[C]//9th Spanish Portuguese Congress on Electrical Engineering，Marbella，2005.