光伏阵列多峰最大功率点跟踪研究

崔岩， 白静晶

(汕头大学工学院，广东汕头515063)

0 引言

太阳能丰富、清洁、安全、方便，是目前广泛探索并得到一定发展的一种可再生能源。但是目前光伏组件价格偏高，且转换率比较低，为了降低整个系统的造价并最大限度地利用光伏组件产生的功率，对光伏组件的最大功率点跟踪(maximum power point tracking，MPPT)是有效的途径之一。而传统的MPPT方法是基于光伏阵列的特性及其输出功率曲线的单峰性。但是，由于实际环境的变化，组件输出的伏安特性曲线呈阶梯状，相应的功率曲线呈现多峰状。因此传统的跟踪方法在这种情况下可能失效。此时，光伏组件的能量没有被充分利用，系统效率将大大降低。

对于住宅型光伏发电系统，由于光伏阵列安装的位置和环境特殊，局部阴影问题尤为突出。不少的研究人员对局部阴影条件下的最大功率跟踪问题进行过研究，也相应地提出了若干解决方案。目前对于光伏阵列在局部阴影条件下MPPT算法主要有:并联功率补偿法、复合MPPT法、电流扫描法、短路电流脉冲法、Fibonacci搜索法和状态空间法等。但是这些算法不是对光伏阵列参数的依赖度较强，实现起来比较复杂［1－5］。

相比之下，人工神经网络不需要任何光伏阵列的物理定义，并且具有很好的非线性映射能力［6］。但是它的缺点是收敛速度慢，目标函数存在局部极小点。但是遗传算法具有很强的宏观搜索能力和良好的全局优化性能，将遗传算法和神经网络相结合，训练时先用遗传算法对神经网络的权值、阈值进行寻找，将搜索范围减小后，再利用神经网络进行精确求解，达到全局搜索和快速高效的目的。可以避免局部极小问题，从而增强在搜索过程中自动获得和积累搜索空间信息及应用控制搜索过程的能力，使结果的性质得以极大改善［7］。

1 被部分遮挡的串联光伏组件特性分析

1.1 光伏组件数学模型

单体光伏电池的模型图如图1所示，I－V特性方程为

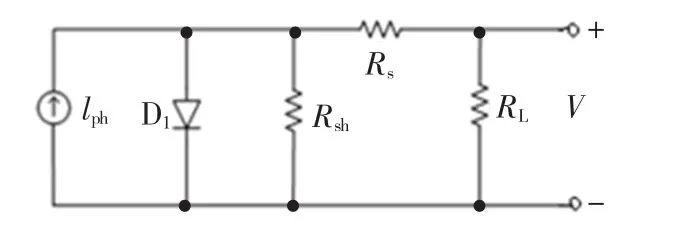
图1 单体光伏电池的等效电路Fig．1 Equivalent circuit of photovoltaic cells

实际应用的光伏阵列在串联回路中每一个光伏电池组件都并联一个二极管，称为旁路二极管，当其中某个组件被阴影遮挡或者出现故障而停止发电时候，在该二极管两端形成正向偏压，这样不至于影响其它正常组件发电，同时也保护光伏电池免受较高的正向偏压或发热而损坏。

图2给出了安装有旁路二极管的光伏组件串联支路的模型图。

图2 安装旁路二极管的光伏组件串联支路模型Fig．2 Serial PV module with bypass diode

当光伏组件中单体光伏电池所接收的太阳辐射均等(无遮挡)时，其输出的功率电压曲线呈单峰状。然而，在很多情况下，由于某组件被阴影遮挡或出现故障时，组件输出的功率电压曲线极有可能呈多峰状。

图3所示，从串联组件中取出两个电池组件，每个电池组件的参数是相同。根据电路理论，在均匀光照条件下，他们的工作电流是一样的，此时旁路二级管处于阻断状态。但当光照条件不相同时，旁路二极管的状态也相应的发生变化。由于系统加入旁路二极管，整个串联组件的电流特性发生了变化，其伏安特性可以用分段函数［11］表示，即

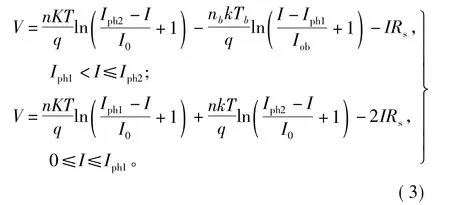
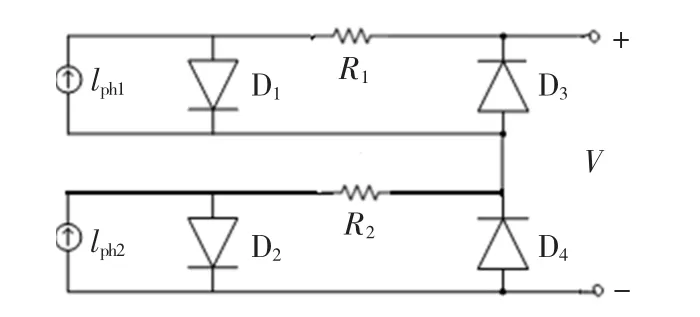
图3 安装旁路二极管的串联太阳能电池组件电路模型图Fig．3 Circuit model figure of serial PV modules with bypass diode

根据输出功率P=IV，可以得到相应的功率特性方程，其同样也是一个分段函数［11］，即

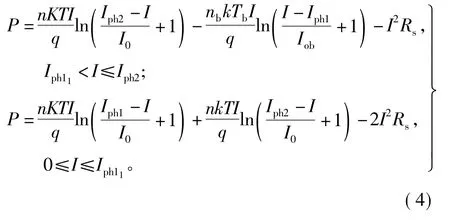
式中:Iph1和Iph2分别是电池组件1和2的光生电流;I0为反向饱和电流;n为二极管的影响因子;q为电子电荷常数(1.6×10－19C);T为热力学温度(K);k为波尔兹曼常数 (1.38×10－23J/K)。其中所用到的太阳能电池特性参数为:在T=25℃时 Isc=3.66 A，Voc=37.58 V，Io=0.025 μA，Rs=0.75 Ω，旁路二极管选用整流型二极管，选取Iob=5.95 μA。

根据串联电路的P－I关系式，由dP/dI=0很容易地找到他的最大功率点，因为分段函数的性质，这时可以求解出两个值。这说明组件在被遮挡的情况下，传统的MPPT方法的已经失效。

1.2 模型特性分析

利用Matlab仿真平台，把光伏组件的相关参数代入上述数学模型中，编出程序，仿真得出有部分遮挡条件下串联光伏组件的伏安特性曲线和功率特性曲线。其仿真图形如图4和图5所示。图4和图5分别是标准光照强度(1 000 W/m2)下3种不同遮挡模式条件下对应的光伏组件的输出伏安特性曲线和功率曲线。其中模式1为无遮挡，模式2(组件1遮挡率为75%，组件2无遮挡)和模式3(组件1遮挡率为85%，组件2遮挡率为50%)为部分遮挡。由图可以很清楚的看到，在无遮挡情况下，系统输出的伏安特性曲线为膝状，功率输出曲线为单峰，而当系统存在遮挡的时候，伏安特性曲线为阶梯状，相应的功率电压曲线为多峰状。

因此，从上述的仿真曲线可以清楚的看出，在光照不均匀条件下，光伏组件的特性曲线有了很大的变化。此时运用传统的最大功率跟踪方法可能会让系统工作在某一个局部峰值附近，而无法确保系统工作在最大的峰值上。所以，在此基础上，提出了一种新的多峰最大功率跟踪算法。

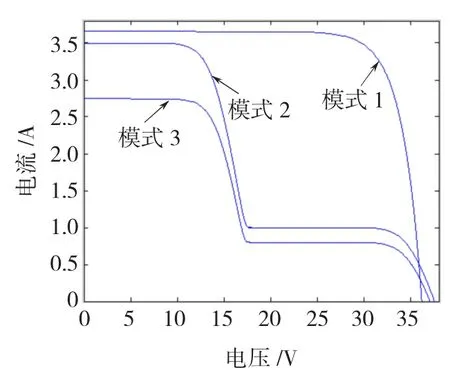
图4 3种不同遮挡模式下的光伏组件输出伏安特性曲线Fig．4 The V-I characteristics curve of the PV output in three different occlusion modes

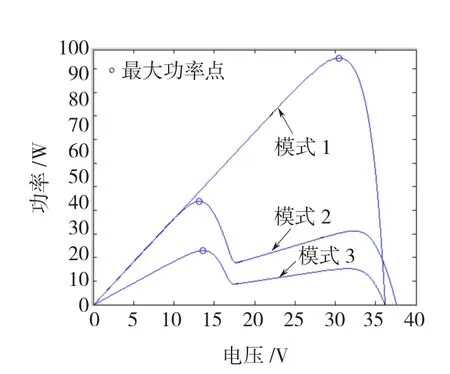
图5 3种不同遮挡模式下光伏组件的输出功率电压曲线Fig．5 The PV characteristics curve of the PV output in three different modes

2 基于遗传神经网络的光伏阵列MPPT模型仿真与预测

2.1 遗传神经网络算法

人工神经网络作为人工智能研究的一种方法，具有较强的非线性映射能力［12］，常用的神经网络BP算法是基于梯度下降这一本质的，因此不可避免地带来以下3个缺点:1)学习过程收敛速度慢;2)容易陷入局部极小点，算法不完备;3)鲁棒性不好，网络性能差。BP网络虽然能够保证网络学习过程的收敛，但是存在这明显的局限性，网络可能得不到全局最优解。而遗传算法具有全局优化能力，适用于多峰函数。为使网络结构性能达到最优，可以利用遗传算法优化神经网络的结构和连接权值。

2.2 BP神经网络建模

根据人工神经网络理论及实际解决问题的需要，设计了光伏阵列MPPT的BP神经网络模型，其中输入量为光强 (Suns)、温度(T)、串联组件1的遮挡率(a)和组件2的遮挡率(b)构成了4维输入向量X，输出为光伏阵列最大功率点的输出电压(V)。

在BP网络中，隐层节点数的选择非常重要，他对建立的神经网络模型的性能影响很大，但是目前理论上并没有一个明确的结论。在本文设计隐层节点数时，通过对不同神经元数进行训练比较，得出误差最小时的隐层的个数。

2.2.1 遗传算法优化BP神经网络

遗传算法优化神经网络，主要是先训练已知结构的网络，然后再优化网络的连接权值，遗传算法以适应度函数为依据，算法从一组随机产生的初始种群开始，反复经过选择、交叉和变异三种遗传操作，不断进化，是个迭代搜索过程。当达到确定的代数或者是达到可接受的结果时，算法停止。

遗传算法优化网络初始权值是为了避免网络训练落入局部极小值，从而提高网络的拟合和预测的精确度。

GA－BP优化的基本思路是:先利用GA搜索空间的一群个体，构成不断进化的群体序列，以某种评价方式得到具有全局性的最优解，然后利用这些解设计神经网络，利用BP神经网络得到问题的最优解。其具体算法如下:

1)解空间内编码，构造适应度函数;

2)初始化种群;

3)根据个体的适应度，对群体中的个体进行选择、交叉和变异操作;

4)根据一定的终止准则，在进行k次操作后，选取m个具有全局性的进化解;

5)以m个进化解为初始解，设计BP神经网络，获得神经网络的权值和阈值;

6)训练神经网络;

7)得到满足精确度要求的最优解，即可得问题的优化解。

2.3 光伏阵列MPPT的网络仿真及结果分析

数据采集采用2004年3月14日6点至18点汕头市的光照和相对应的温度，如图6、图7所示。

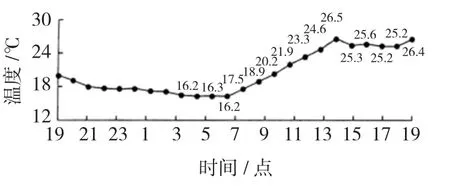
图6 时间—温度图Fig．6 Time-temperature chart

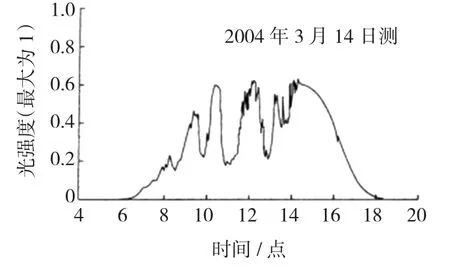
图7 时间—光照图Fig．7 Time-illumination figure

在不同的光照强度、温度及不同的遮挡条件下，结合上述光伏组件数学模型，运用Matlab提供的神经网络相关函数和遗传算法工具箱函数编写程序，计算出不同环境条件下对应的最大功率点的电压。在本论文中，整理得出12组数据作为训练数据，以下是对光伏组件多峰最大功率点的网络仿真。

从图8和图9可以清楚的看出，经过遗传算法对神经网络的权值的优化和修正，使得整个系统的预测结果更为准确，其误差值基本上都在5%以内。

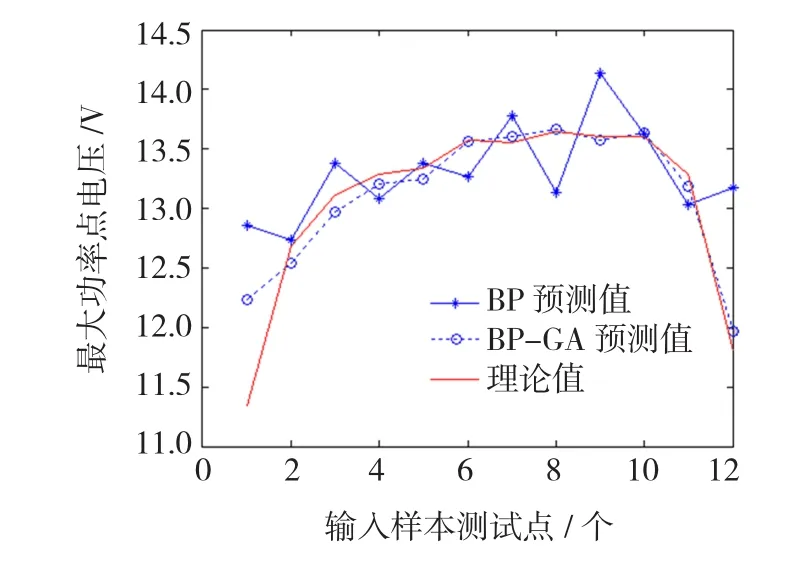
图8 网络预测Fig．8 Network forecast map

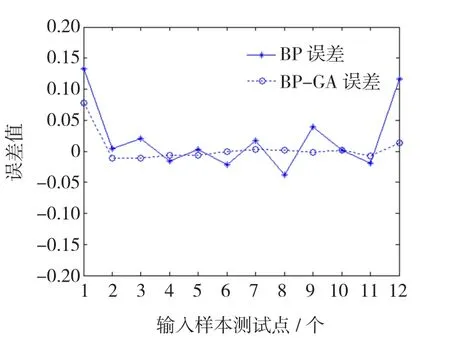
图9 网络预测误差Fig．9 The error chart of the network prediction

衡量预测效果的一个重要指标是平均误差，定义为

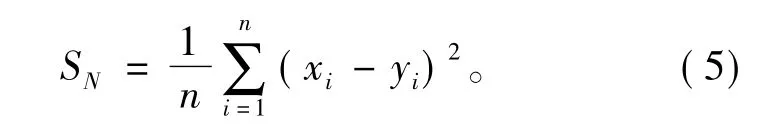
预测值和真实值之间的差值可能是负数，所以先平方。SN数值越小说明预测值越准确，即预测越成功。其中，n表示预测的数目，xi为实际值，yi为预测值。

预测的12组最大功率点的电压与实际值的平均误差SN=0.002 1，而没有优化之前的BP网络的平均误差SN=0.156 0。由此可说明GA-BP的预测效果更好，预测的精确度更高。

3 结语

遗传神经网络模型结合了遗传算法的全局性和BP神经网络的并行性，克服了遗传算法收敛至最优解的速度较慢和神经网络易陷入局部解的缺陷。解的全局性由遗传算法提供，神经网络则保证了求解的快速性，是一种效率较高、求解有效的优化算法。本文采用改进的BP神经网络算法，结果表明，在多峰最大功率追踪方面，预测效果非常好。作为光伏发电的一部分，光伏最大功率点电压的预测分析发挥了重要作用，这为以后整个硬件电路的设计打下了良好的基础。

［1］ SHIMIZU T，M HIRAKATA M，TKAMEZAWA T，WATANABE H．Generation control circuit for photovoltaic modules［J］．IEEE Trans on Power Electronic，2001，16(3):293－300．

［2］ KOBAYASHI K，TAKANO I，SAWADA Y．A study on a two stage maximum power point tracking control of a photovoltaic system under partially shaded insolation conditions［C］//2003 IEEE Power Engineering Society General Meeting，Conference Proceedings．2003，4:2612 －2617．

［3］ TOSHIKO Noguchi，SHIGENORI Togashi，RYO Nakamoto．Shortcurrent pulse-based maximum power point tracking method for multiple photovoltaic and converter module system［J］．IEEE Trans on Industrial Electronics，2002，49(1):217－222．

［4］ MIYATAKE M，INADA T，HIRATSUKA I，et al．Control characteristics of a Fibonacci search based maximum power point tracker when a photovoltaic array is partially shaded［C］//Power Electronics and Motion Control Conference．2004，2:816－821．

［5］ SOLODOVNIK E V，LIU S，DOUGAL R A．Power controller design for maximum power tracking in solar installations［J］．Trans on Power Electronics，2004，19(5):1295 －1304．

［6］ KARATEPE E，BOZTEPE M，COLAK M．Development of a suitable model for characterizing photovoltaic arrays with shaded solar cells［J］．Sol Energy，2007，81(8):977 － 992．

［7］ 雷英杰，张善文，李续武，等．Matlabl遗传算法工具箱及应用［M］．西安:西安电子科技大学出版社，2005:67－73．

［8］ 余世杰，何慧若．太阳能的光伏利用［M］．合肥:合肥工业大学出版社，1991:6－17．

［9］ 苏建徽，余世杰，赵为，等．硅太阳电池工程用数学模型［J］．太阳能学报，2001，22(4):409 －412．SU Jianhui，YU Shijie，ZHAO Wei，et al．Investigation on engineering analytical model of silicon solar cells［J］．Acta Energiae Solaris Sinica，2001，22(4):409－412．

［10］ DING Jinlei，CHENG Xiaofang，FU Tairan．The analysis of series resistance and P-T characteristic of solar cell［J］．Vacuum，2005，77(2):163 －167．

［11］ 翟载腾，程晓舫，丁金磊，等．被部分遮挡的串联光伏组件输出特性［J］．中国科学技术大学学报，2009，39(4):398 －402．ZHAI Zaiteng，CHENG Xiaofang，DING Jinlei，et al．Characteristics of partially shadowed serial PV module output［J］．Journal of University of Science and Technology of China，2009，39(4):398－402．

［12］ 苏全明，张莲花 刘豉，等．MATLAB工具箱应用［M］．北京:电子工业出版社，2004:40－45．