直接转矩控制的无刷双馈感应电机的异步启动

张爱玲， 许永顺， 王昕

(太原理工大学电气与动力工程学院，山西太原030024)

0 引言

和双馈电机(doubly fed induction machine，DFIM)相比，无刷双馈电机(brushless doubly－fed machine，BDFM)由于无刷而受到人们的青睐。在一些特殊的应用领域，例如在风力发电及大功率变速驱动领域BDFM有着明显的技术优势，逐渐显现出取代DFIM的可能性［1－7］。按转子结构的不同BDFM可以分为无刷双馈磁阻电机和无刷双馈感应电机(brushless doubly－fed induction machine，BDFIM)。近5年来BDFIM的控制方法取得了令人瞩目的进步。其中文献［1－3］提出了BDFIM的矢量控制策略，发电［1，3］及电动状态［2］的实验结果证明了控制策略的可行性，并获得了令人满意的稳态及动态性能。文献［4］利用解析表达式深入分析了BDFIM直接转矩控制策略的可行性，且电动状态的实验结果和理论分析十分吻合。上述两种方法均可用于对动态性能要求较高的场合。文献［5］研究了控制绕组相位角控制策略，该方法可用于对动态性能要求不高的风机和泵类负载。

启动方法和启动性能是任何种类电动机的重要性能之一，但是对于无刷双馈电动机启动性能的研究却比较少。文献［2－4］虽然给出了电动状态的实验结果，但并未述及所使用的启动方法。文献［5－6］提出了一种异步启动方法，该方法将启动过程分为异步启动和牵入同步两个阶段，即启动时将控制绕组短接，功率绕组直接接入电网，当电机转速接近同步速时，再将控制绕组接入逆变器使电机双馈运行，转速被牵入同步，文献［5］给出了该方法的实验结果。文献［6］采用反馈线性(feedback linearization)控制方法，文献［7］采用速度开环的v/f控制方式对异步启动及牵入同步的动态过程进行了仿真计算。但文献［5－7］对异步启动过程的电流及转矩均未做理论分析，也未述及如何根据所采用的控制策略改善牵入同步时的动态性能。

深入研究了基于直接转矩控制策略的BDFIM的异步启动方法。利用等效电路分析了异步启动阶段的性能。为了减小牵入同步时两个定子绕组的冲击电流，提出一种磁链优先的控制方法，并在样机上进行实验。

1 异步启动方法

无刷双馈电机在双馈运行方式下的接线图如图1所示，功率绕组接工频电源，控制绕组由交－直－交逆变器供电。

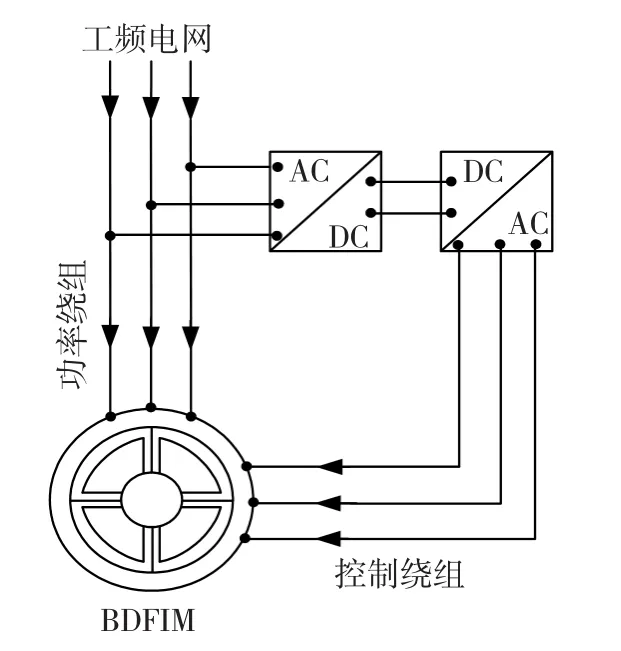
图1 BDFIM运行示意图Fig．1 BDFIM operation

异步启动时，功率绕组接线不变，控制绕组短接(通过逆变器3个导通的下桥臂实现)，如图2(a)所示。转速达到同步速附近时，控制逆变器使电机进入双馈运行状态，如图2(b)所示。在合适的控制方式下，转速达到给定值同步运行。

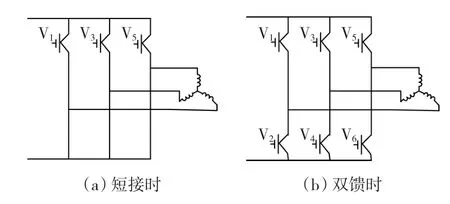
图2 BDFIM控制绕组接线图Fig．2 Configuration of control winding for BDFIM

2 异步启动电流及启动转矩的分析

2.1 异步启动电流的分析

图3为BDFIM的双T型等效电路［8］，图中所有参数都已折算到功率绕组，Up，U″c分别为功率绕组和控制绕组电压;Ip，I″c和 I'r分别为功率，控制和转子绕组电流;Rp，R″c，和 Rr分别为功率，控制和转子绕组电阻;Xlp，X″lc，X'lr分别为功率，控制及转子绕组的漏抗;Mp，M″c分别为功率绕组，控制绕组与转子绕组之间的互感;ωp为功率绕组角频率;sp，sc和s为转差率，其表达式为

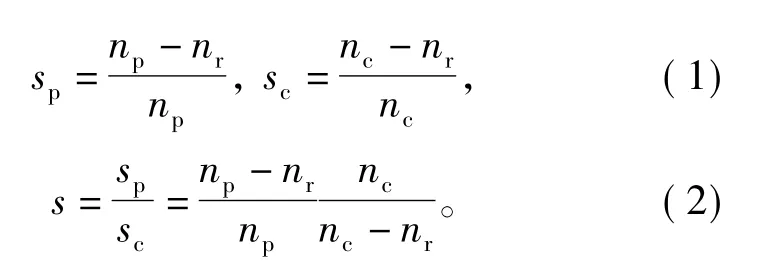
式中:np，nc分别为功率绕组和控制绕组的同步转速，由两个绕组各自的频率决定;nr为转子转速。启动瞬间 nr=0，图3 中 U″c=0，s=sp=1，且由于互感远大于漏感，分析启动电流时可认为Mp和M″c所在的支路断开，则启动瞬间的等效电路如图4所示。

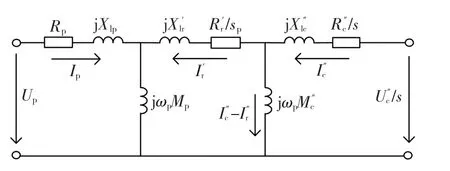
图3 BDFIM的双T型等效电路Fig．3 Double T equivalent circuit for BDFIM

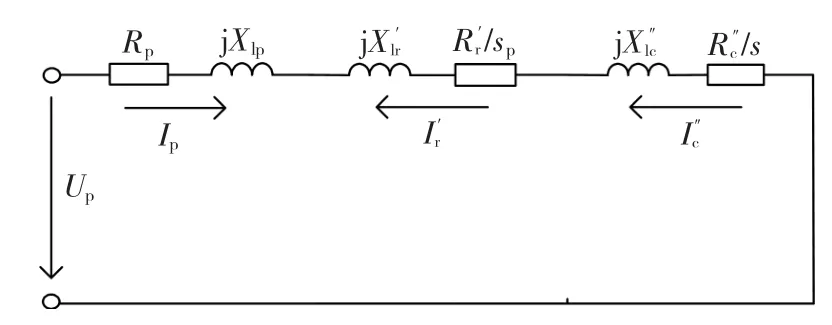
图4 BDFIM的简化等效电路Fig．4 Simplified equivalent circuit for BDFIM

由图4可得启动瞬间功率绕组的电流为

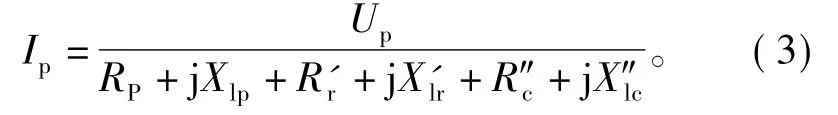
式(3)和感应电机启动电流的表达式相比，式(3)的分母中多了控制绕组的电阻和漏抗，且由于BDFIM的定子槽中嵌放着两个绕组，其漏抗Xlp，X″lc与感应电机相比较大，因此功率绕组启动电流约为同容量感应电机的2/3～1/2。

由图3可知，控制绕组的启动电流为

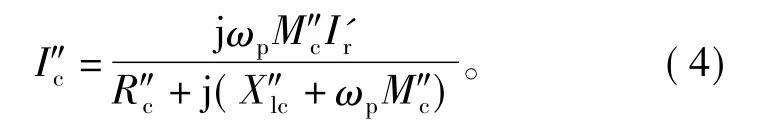
式(4)中的分子为转子电流引起的控制绕组的感应电势。由式(3)和式(4)可知，在控制绕组中串电阻可以有效减小两个定子绕组的启动电流，但无疑增加了启动设备及启动方法的复杂性。和感应电机一样，随着转速的增加，3个绕组的电流都将减小，达到同步速附近稳定运行时的电流取决于负载，若电机空载，控制绕组稳定时的电流趋于零。

2．2 启动转矩的分析

不计定子电阻时，无刷双馈电机稳态运行时电磁转矩的一般形式［8］为

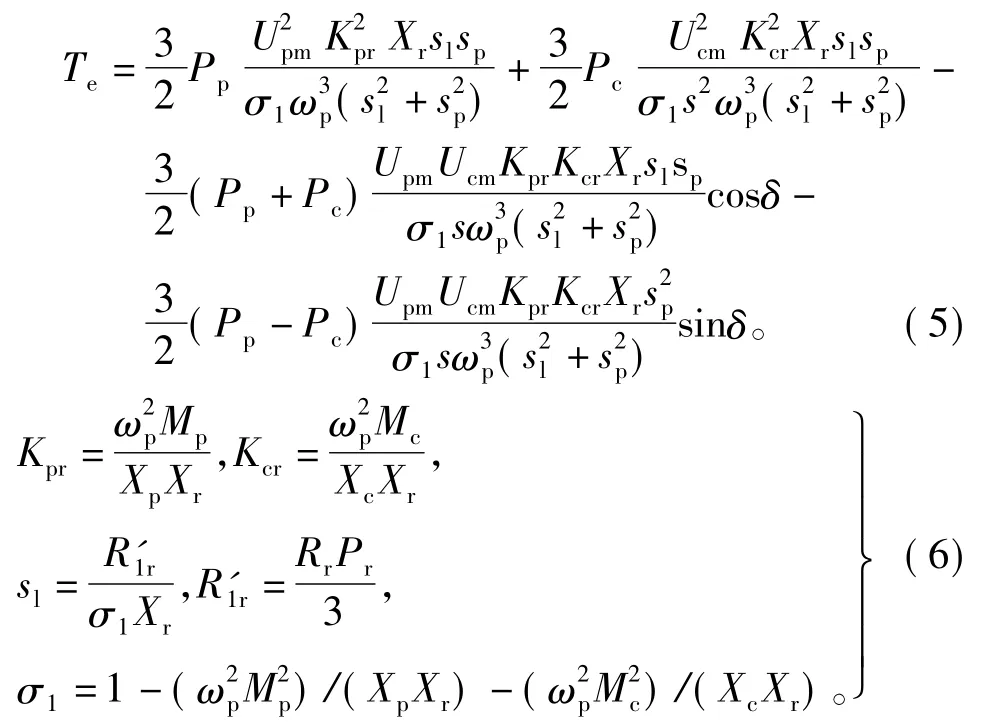
式中:Pp为功率绕组极对数;Pc为控制绕组极对数;Xr为转子电抗;Mc为控制绕组与转子之间的互感;Xp为功率绕组电抗;Xc为控制绕组电抗;Rr为转子电阻;Pr为转子极对数;δ为功率绕组与控制绕组电压之间的夹角;Upm和Ucm分别为功率绕组和控制绕组电压的幅值，以上参数均未进行绕组折算［8］。异步启动时，式(5)中 Ucm=0，sp=1，再将 s1和R'1r代入，则启动转矩为

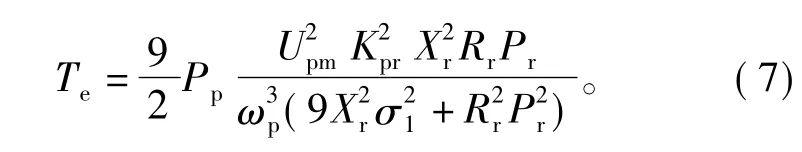
由式(7)可知，启动转矩和电压的平方及电机参数有关，与感应电机相似。

3 无刷双馈电机直接转矩控制的原理

3.1 基本原理

BDFIM直接转矩控制系统的结构如图5所示［4］，功率绕组接380 V工频电源不可控，控制绕组由变流器供电。

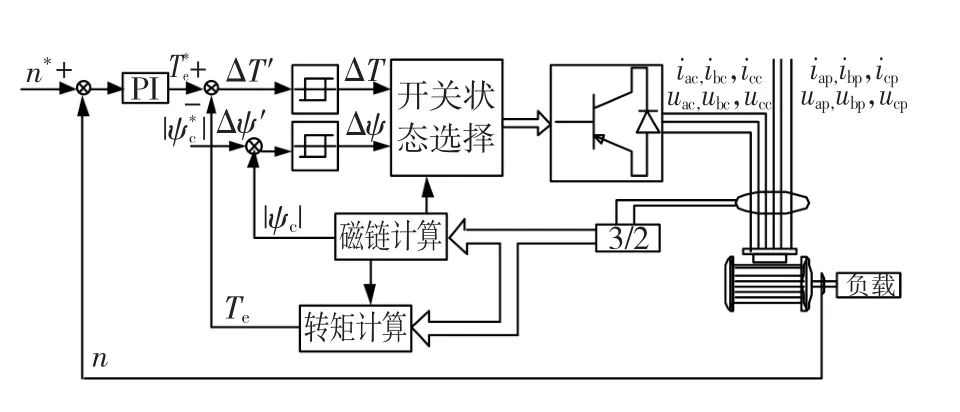
图5 直接转矩控制系统结构Fig．5 Schematic of DTC control for BDFIM

3.2 开关表

系统开关表如表1所示［4］。

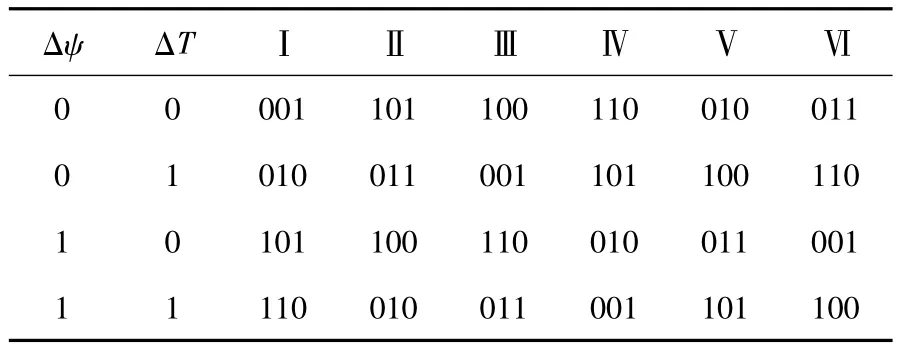
表1 开关表Table 1 Switch table

扇区的划分如图6所示，表1中Ⅰ～Ⅵ为控制绕组磁链所在的扇区，由其 α，β 分量 ψαc，ψβc计算。表1中当ΔT'≥εT时，ΔT=1，表示需要增加转矩，否则，ΔT=0，表示需要减小转矩;同理，当 Δψ'≥εψ时，Δψ =1，否则，Δψ =0。εT，εψ分别为转矩和磁链滞环比较器的环宽。该开关表可以同时满足转矩及磁链增加或减少的需要。

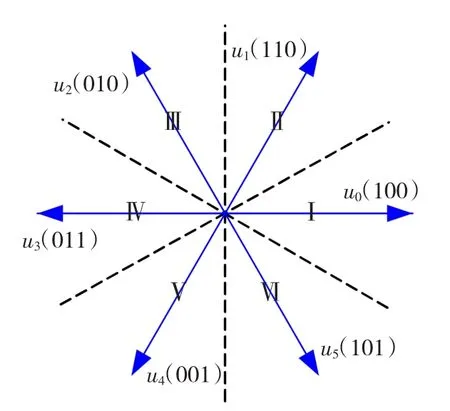
图6 扇区划分Fig．6 The sector partition

4 牵入同步运行

当电机转速接近同步速时，控制逆变器使系统进入双馈运行状态。由于控制绕组由短接改为由逆变器供电时，必然存在磁链的建立过程，同时给定转速与实际转速之间的偏差也必然使ΔT较大。虽然使用表1可以同时兼顾磁链及转矩增加或减小的需求，但是使用如表2所示的磁链优先的开关表进行预励磁，可以在切入双馈的瞬间，使磁链先建立起来，这样可以有效减小切入双馈时的电流，当磁链达到给定的阈值时，再改用开关表1进行控制。

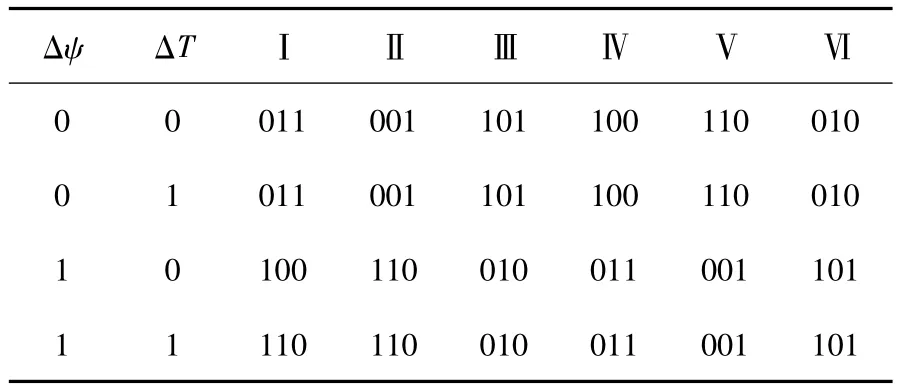
表2 磁链优先开关表Table 2 Switch table with flux priority

磁链优先开关表的设计思想是，当磁链比给定值小很多时，采用与磁链处于同一扇区的空间电压矢量，使磁链快速增加。控制绕组的电压方程［4］(在控制绕组坐标系下)为

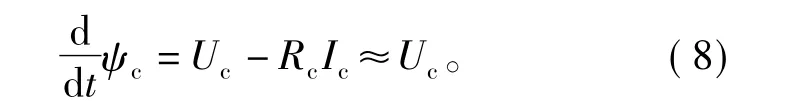
将式(8)离散化后可得

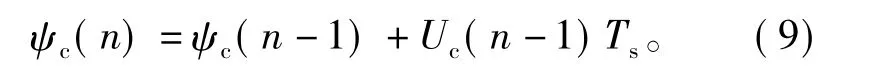
式中:Uc，ψc和Ic分别为控制绕组电压，磁链及电流的空间矢量;Rc为控制绕组电阻;Ts为采样周期。用矢量三角形描述式(9)，如图(7)所示。

图7 定子磁链与电压矢量Fig．7 stator flux and voltage vector

设某一瞬间磁链空间矢量ψc位于第Ⅰ扇区，使用与其位于同一扇区的空间矢量u0，如表2所示，可使电压矢量和磁链的夹角最小，从而使磁链增加最快。同理，采用与磁链间隔两个扇区的空间电压矢量，使磁链减小最多。

5 实验研究

5.1 实验装置

为了验证本文所提方法的正确性，在交流电机实验平台上对BDFIM样机进行异步启动实验。样机采用笼型转子，4组同心式短路线圈，每组5个短路环。功率绕组参数为:3对极;额定功率为3 kW;额定电压为380 V;额定电流为6.9 A。控制绕组参数为:1对极;额定电压为380 V;额定电流为3.4 A;同步转速为750 r/min。

实验平台如图8所示，直流发电机作为BDFIM的负载，扭矩传感器用来测量BDFIM的输出转矩，使用OMRON增量式E6C2－CWZ6C光电编码器测量转速，由霍尔电流传感器测量电流。

实验中功率绕组接380 V工频电源，控制绕组接双PWM变流器，图9为其结构示意图。两个变流器的控制系统相似，图中只画出电机侧变流器控制系统。数字信号处理芯片(digital signal processor，DSP)TMS320LF2407A是控制系统的核心，其通讯接口CAN及PC机的USB接口通过USBCAN接口卡相连，实现DSP与PC机之间的数据交换。例如，转速及磁链等给定值可以由PC机发送到DSP，电流、转矩等采样值及计算值也可以由DSP发送到PC机。实验中系统采样周期Ts=280 μs，CW磁链给定

图8 实验装置Fig．8 Experimental setup

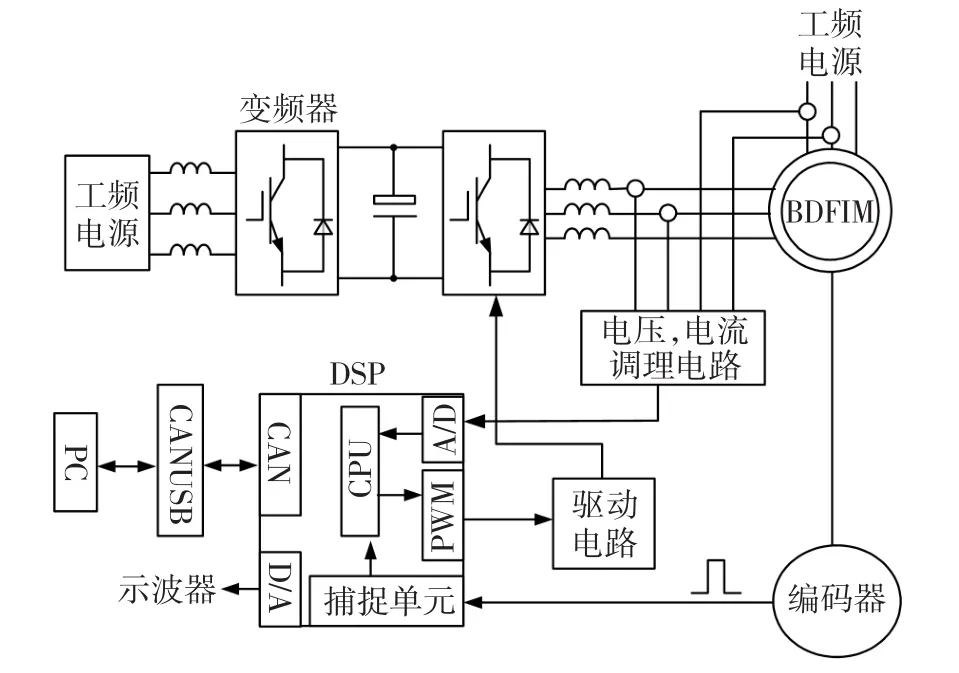
图9 变流器结构Fig．9 Schematic diagram of the converter

5.2 实验结果

5.2.1 异步启动阶段的实验结果

图10(a)～图10(d)分别为额定电压下空载异步启动时控制绕组、功率绕组电流，转速及电磁转矩的波形。其中功率绕组电流的峰值为17.5 A，约为其额定电流峰值的2.34倍。控制绕组电流的峰值为11.5 A，约为其额定电流峰值的2.48倍，两个绕组的电流均随着转速的上升衰减。由于电机空载，控制绕组的电流稳态时接近零，转速接近同步速即750 r/min;启动瞬间，电磁转矩波动较大，原因有待进一步分析。

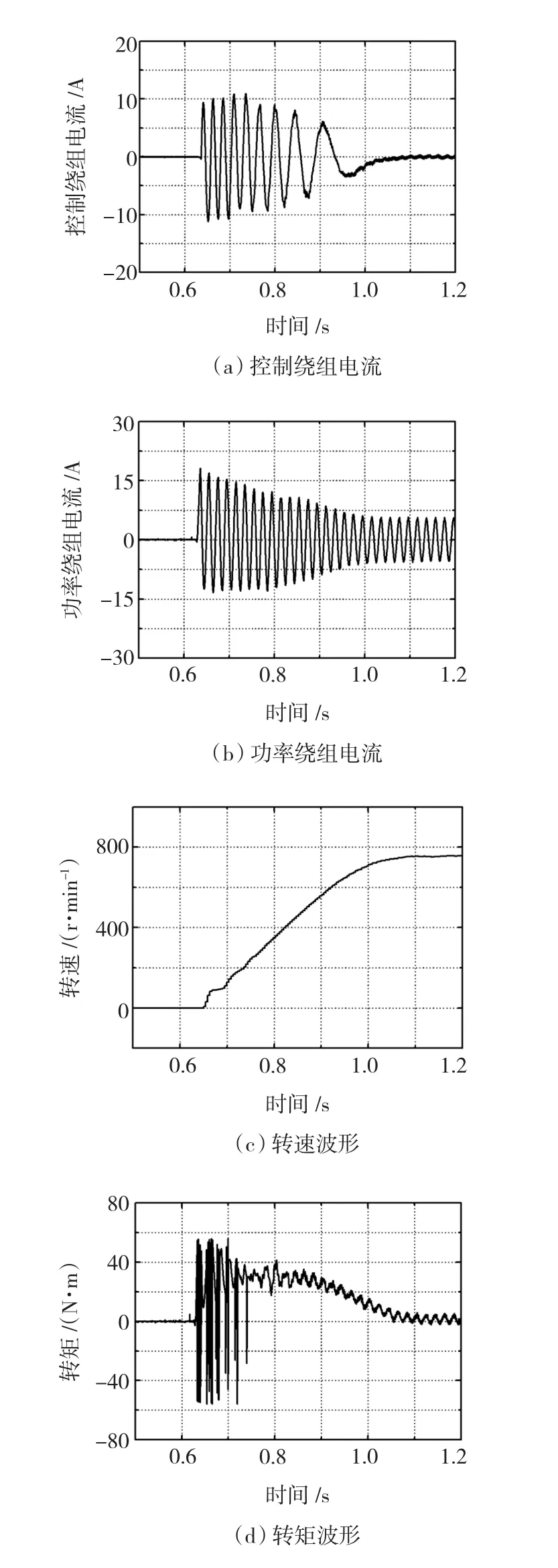
图10 启动时的实验结果Fig．10 Experimental results for starting

5.2.2 牵入双馈运行的实验结果

电机由异步牵入双馈时，将采用表1和磁链优先两种控制方法的实验结果进行对比。采用后一种方法当控制绕组磁链达到0.92 Wb时，开关表切入表1。两种方式下，给定转速均为795 r/min，其他实验条件相同，图11为由异步牵入超同步的实验结果。

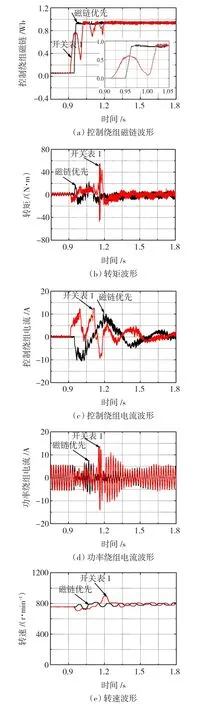
图11 从异步牵入超同步的实验结果Fig．11 Experimental results from asynchronous to synchronous model

由图11(a)可知，采用磁链优先方法时，磁链单方向平稳增加，达到给定值的时间约为25 ms;由图11(b)可知，两种方法下，电磁转矩的大小没有明显区别，这是由于建立磁链所需的时间很短;由图11(c)和图11(d)可知，采用磁链优先方法时，两个定子绕组的电流明显减小。另外采用如表1所示的控制方式，在接近1.2 s时，由于磁链的跌落，引起功率绕组电流、转速和转矩的振荡。实验结果表明，当磁链比给定值小很多时，优先控制磁链会取得较好的控制效果。

6 结语

本文利用稳态等效电路分析了BDFIM异步启动时的电流，理论分析和样机的实验结果表明，额定电压下的直接启动电流小于同容量的感应电机。为了减小牵入同步时两个定子绕组的冲击电流，提出了一种磁链优先的控制方法，样机的实验结果验证了所提控制方法的有效性。

［1］ SHAO Shiyi，EHSAN A，FARHAD B，et al．Stator-flux-oriented vector control for brushless doubly fed induction enerator［J］．IEEE Transactions on Industry Electronics，2009，56(10):4220 －4228．

［2］ POZA J，OYARBIDE E，SARASOLA I，et al．Vector control design and experimental evaluation for the brushless doubly fed machine［J］．IET Electric Power Applications，2009，3(4):247 －256．

［3］ KOSTYANTYN P，DEWEI X．Modeling and control of brushless doubly-fed induction generators in wind energy applications［J］．IEEE Transactions on Power Electronics，2008，23(3):1191－1197．

［4］ SARASOLA I，POZA J，RODRIGUEZ M A，et al．Direct torque control design and experimental evaluation for the brushless doubly fed machine［J］．Energy Conversion and Management，2011，52(2):1226－1234．

［5］ SHAO Shiyi，ABDI E，MCMAHON R．Operation of brushless doubly-fed machine for drive applications［C］//4th IET International Conference on Power Electronics，Machines and Drives，PEMD 2008，April 2 －4，2008，York，United kingdom．2008:340 －344．

［6］ DING Feng，ROBERTS P，RICHARD M．Control study on starting of BDFM［C］//41st International Universities Power Engineering Conference，UPEC 2006，September 6－8，2006，Newcastle upon Tyne，United kingdom．2006:660－664．

［7］ 邓先明，张海忠，拾华杰．笼型转子无刷双馈电机启动特性分析［J］．电机与控制学报，2008，12(5):545－549．DENG Xianming，ZHANG Haizhong，SHI Huajie．Analysis of starting characteristics of cage-rotor brushless doubly-fed machine［J］．Electric Machines and Control，2008，12(5):545 － 549．

［8］ 章玮．无刷双馈电机系统及其控制研究［D］．杭州:浙江大学电气工程学院，2001．