高空电推进系统的积分滑模反演速度控制

杨前， 刘卫国， 骆光照

(西北工业大学自动化学院，陕西西安710129)

0 引言

随着现代科学技术的进步，高空环境独特的资源优势已成为各国关注的热点。对于高空飞艇、高空无人机这一类飞行器而言，由于高空大气稀薄，典型的电推进系统只能由电池、高性能控制器、高效逆变器、高功率密度永磁同步电动机(permanet magnet synchronous motor，PMSM)、减速器以及螺旋桨等组成［1］。

在高空环境中，电推进系统的控制模型会发生变化，主要因为电推进系统散热困难。温度、外界大气参数的扰动以及供电系统和储能系统参数的改变都会引起PMSM的系统参数发生变化;同时，电推进系统的输出转矩必须承受定常、非定常的负载扰动［2－3］。如何克服系统参数摄动带来的不利影响是PMSM控制研究的关键。

文献［4］研究了PMSM交流调速系统的空间矢量脉宽调制(space vector pulse wide modulation，SVPWM)控制方法;文献［5］设计了PMSM的反演速度控制器，但没有考虑系统参数变化;文献［6－9］将滑模方法应用于PMSM控制系统中，文献［6］将带转矩观测器的模糊滑模控制器用于PMSM速度控制系统中，提高了系统的动态性能，文献［8］采用高阶终端滑模控制器，削弱了控制量的抖振，文献［9］采用径向基函数神经网络在线辨识滑模控制器的切换项增益，在减小抖振的同时提高了系统的鲁棒性;文献［10］提出了滑模与反演控制相结合的PMSM速度控制方法，提高了系统对外界干扰的鲁棒性;文献［11－12］将积分反演法用于PMSM位置控制系统中，文献［12］通过积分反演法实现名义模型的位置跟踪，利用全局滑模控制保证飞行模拟转台伺服系统的鲁棒性，而积分反演法在速度控制中应用相对较少;文献［13］通过反演法设计了PMSM的速度跟踪控制器，利用积分因子减小了转速静态误差。

为了解决高空电推进系统用PMSM在参数摄动条件下的转速跟踪控制问题，本文在文献［13］的积分反演速度控制算法研究的基础上，针对PMSM参数摄动情况下的速度跟踪系统，提出一种基于反演的积分滑模控制算法，通过转速误差积分因子来减小电机稳态运行时的转速静态误差，利用指数趋近律构造d－q轴电流误差的滑模面方程来处理系统的不确定性问题，并进行控制器设计。通过Lyapunov稳定性理论进行稳定性分析。对PMSM转速控制系统进行了SIMULINK仿真和硬件在回路(hardware in Loop，HIL)实验，并与反演控制方法进行比较，进一步验证所提方法的有效性。

1 PMSM的数学模型及转速控制问题

假设电动机铁心不饱和，空间磁场呈正弦分布，不计涡流和磁滞损耗，隐极式PMSM基于d－q轴坐标系的数学模型可以表示为

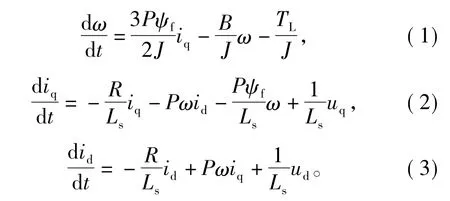
式中:R为定子电阻;Ls为定子电感;P为极对数;ψf为永磁体磁链;J为转动惯量;B为粘性摩擦系数;TL为负载转矩;id，iq和 ud，uq分别为 d、q轴的电流和电压;ω为机械转速。

在实际运行过程中，PMSM的系统参数会随高空环境发生变化，而反演法本身易受调节参数和系统参数的影响，且电机稳态运行时存在转速静态误差;采用积分作用以减小电机稳态运行时的转速静态误差;由于滑模算法的滑动模态可以根据控制需要设计，且滑模运动与被控对象的参数变化以及外界干扰无关［14］，采用积分滑模系统对由参数变化造成的总不确定性进行逼近，并设计了一种基于反演的积分滑模控制器。PMSM转速控制系统的控制目标是转速跟踪误差趋于零，即

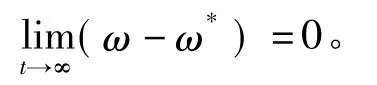
式中ω*为给定的参考转速。

2 PMSM速度积分滑模反演控制器设计

反演法是一种递推设计方法，通过逐步选取虚拟控制函数和构造Lyapunov函数最终得到系统实际的控制律和全局Lyapunov函数，保证系统的全局渐进收敛。在电机控制器设计中，反演控制是对虚拟电流的选择，而电压才是真正的控制输入。

为了获得最大的转矩输出，隐极式PMSM通常采用磁场定向的控制方式，即令直轴参考电流0。定义速度和d、q轴电流子系统的误差函数分别为

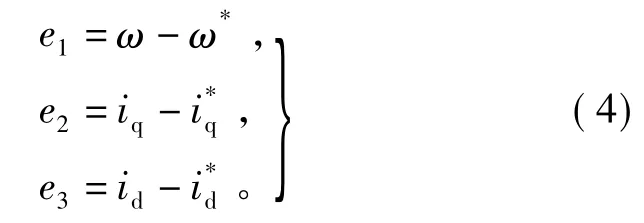
为了获得期望的转速跟踪，选取d、q轴电流为虚拟控制函数，设计速度误差的Lyapunov函数为

由于定子电流变化的反应时间远远快于转速的变化，为了确保当存在系统参数摄动和外界干扰时速度误差能够快速收敛，选用指数趋近律设计q轴电流误差的动态滑模面方程，即

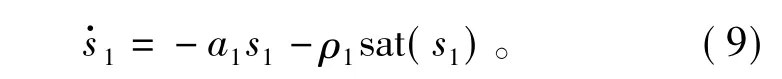
式中，s1=c1e2，且c1＞0，a1＞0，ρ1＞0，sat(s1)为饱和函数。因为理想的滑动模态是不存在的，通过饱和函数使PMSM作准滑动模态运动，可以削弱控制量的抖振。根据式(2)、式(7)、式(8)和式(9)可以间接推导出q轴的实际控制电压为

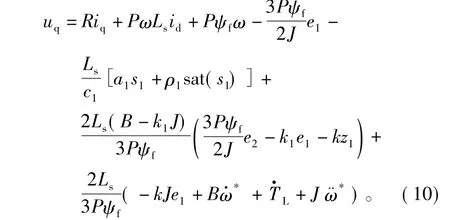
同理，选用指数趋近律设计d轴电流误差的滑模面方程为

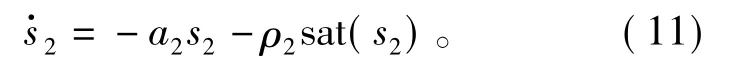
式中，s2=c2e3，且 c2＞0，a2＞0，ρ2＞0。根据式(3)、式(7)和式(11)可以推导出d轴实际的控制电压为

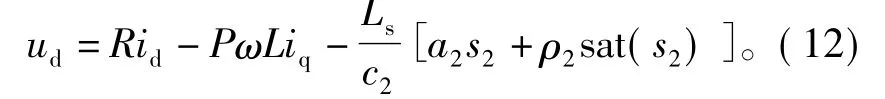
定理 对于由式(1)～式(3)给出的PMSM系统，控制律采用式(10)和式(12)，可以使PMSM系统达到转速的全局渐进跟踪，并且系统全局渐进稳定。

由式(17)和式(19)可知，在电压控制律式(10)和式(12)的作用下，系统达到速度的全局渐进跟踪。

3 仿真研究

本节利用SIMULINK分别采用反演控制方法和所提算法对PMSM矢量控制系统进行仿真。PMSM积分滑模反演控制系统的原理框图如图1所示。

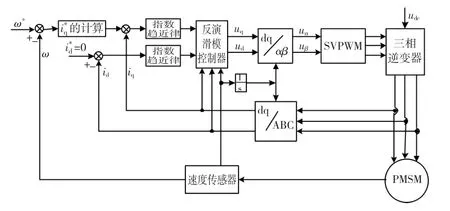
图1 系统控制结构Fig．1 System control configuration

PMSM的标称参数取为:R=1.65 Ω;Ls=0.009 2 H;J=0.001 kg·m2;P=4;ψf=0.175 Wb。所设计的控制器的参数取为:k=15;k1=150;c1=50;c2=500;a1=a2=2 000;ρ1= ρ2=5。

PMSM反演控制器速度环参数k1=100;d－q轴电流环参数k2=k3=2 000。仿真效果如图2和图3所示。

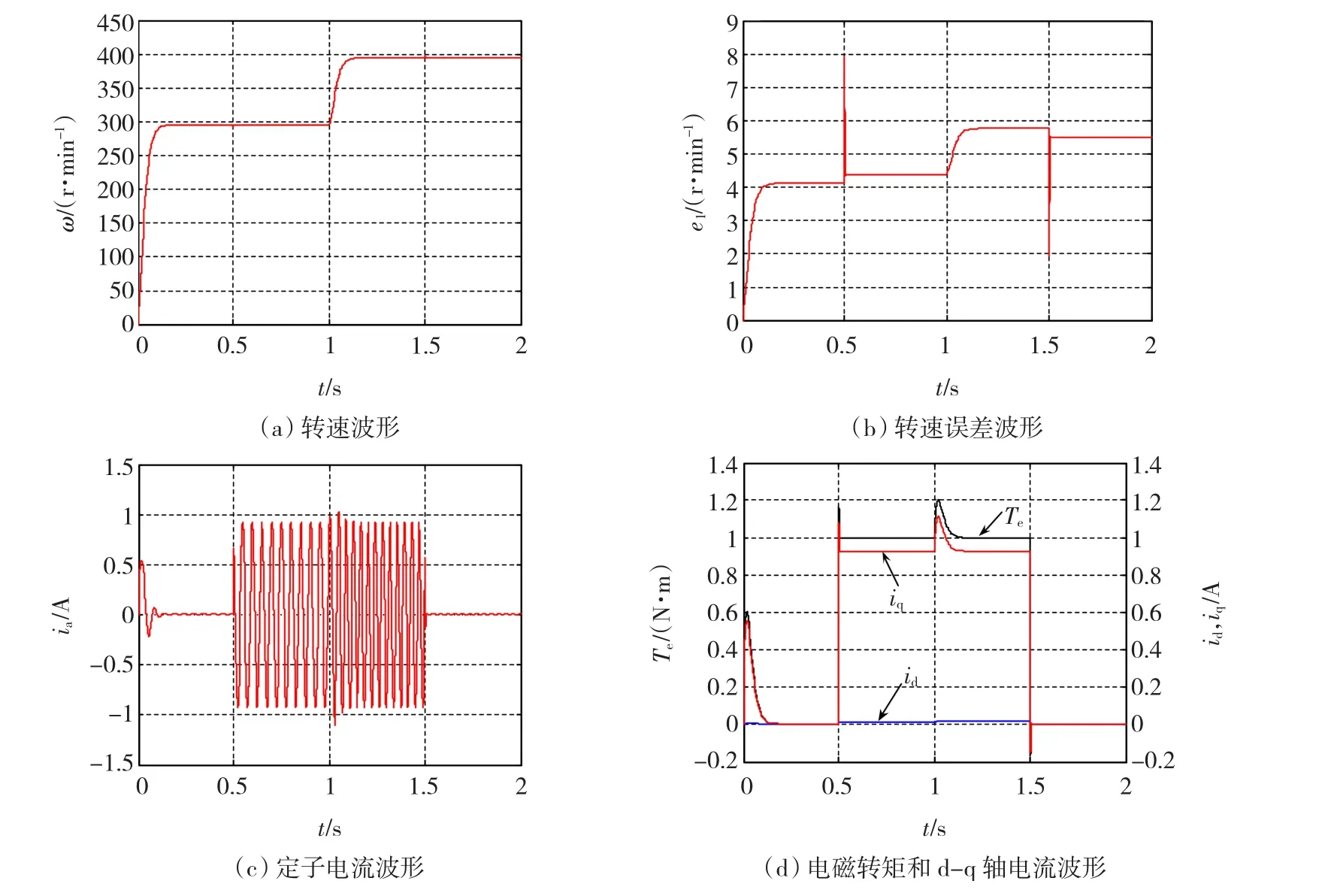
图2 PMSM反演控制系统的仿真波形Fig．2 Simulation waveform of PMSM backstepping control system

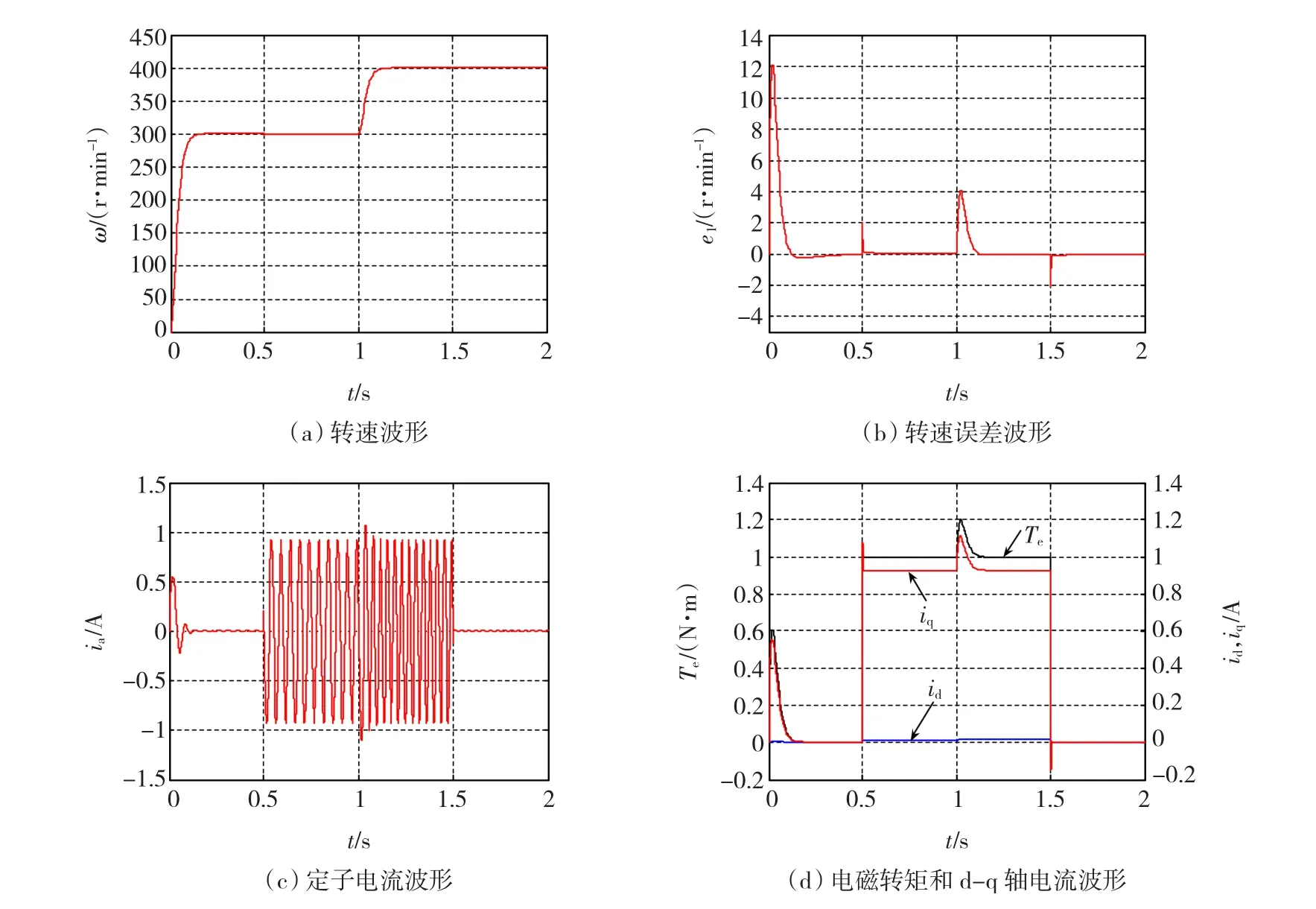
图3 PMSM积分滑模反演控制的仿真波形Fig．3 Simulation waveform of PMSM integral sliding mode backstepping control system

给定初始参考转速为300 r/min，在1 s时，转速上升至400 r/min。在0.5 s时突加1 N·m的负载转矩，在1.5 s时撤消该负载转矩的反演控制仿真波形如图2所示，积分滑模反演控制的仿真波形如图3所示。其中，ia为A相定子电流。

由图2和图3可知，在1 s时，当参考转速由300 r/min上升到400 r/min时，反演控制系统需要0.2 s的过渡时间，由参考转速突变引起的转矩超调小于20%;因为引入转速误差积分因子，积分滑模反演控制系统的转速动态响应很快，仅需0.1 s的过渡时间，由参考转速突变引起的转矩超调也小于20%。在0.5 s时突加1 N·m的负载转矩，反演控制系统由负载转矩突变引起的转速超调为8 r/min，转矩超调小于17%;而积分滑模反演控制系统的转速超调仅为2 r/min，由负载转矩突变引起的转速超调显著降低，只有5%。当PMSM稳态运行时，反演控制系统存在转速静态误差，且转速静态误差随参考转速和负载转矩的增加而增大，而当电机稳态运行时，积分滑模反演控制系统在参考转速和负载转矩突变条件下，均无转速静态误差。因此，积分滑模反演控制算法比反演控制具有更好的动、静态性能，对参数变化和负载干扰具有更好的干扰抑制性能。

4 实验研究

基于dSPACE实验平台的PMSM速度控制系统的HIL实验是将基于不同算法的控制器用实时仿真控制模型代替，电机、编码器以及霍尔传感器等与闭环控制相关的硬件通过实时接口连接到实时仿真控制模型中，构成HIL实验系统［15］。由于仿真模型代替实际的硬件控制电路，实验过程具有多次可重复性。利用ControlDesk可以在线调整控制参数，控制器设计的可靠性大幅提高。硬件在回路实验原理如图4所示。

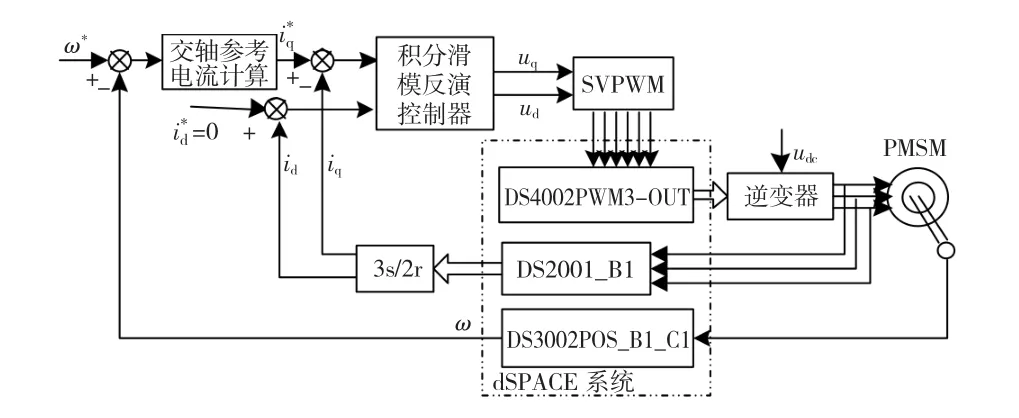
图4 硬件在回路实验系统Fig．4 Experiment system diagram of hardware in loop

DS4002PWM3－OUT模块输出SVPWM变换器产生的6路PWM控制信号经三相电压型逆变器给PMSM供电，DS2001－B1模块实现霍尔电流信号的采集与反馈，DS3002 POS－B1－C1模块实现速度与转子位置信号的采集与反馈，dSPACE系统的采样频率为5 kHz。

给定参考转速为300 r/min，负载转矩为1 N·m，两种控制方式的实验波形如图5和图6所示。

由图5和图6可知，反演控制时，转速静态误差为8 r/min，转速范围为278～308 r/min，转速最大超调为8%;积分滑模反演控制时，无转速静态误差，转速范围为292～308 r/min，最大转速超调为3%。相比于反演控制，负载运行时PMSM积分滑模反演控制系统给定参考转速运行更加平稳，进一步验证了所提算法的有效性。

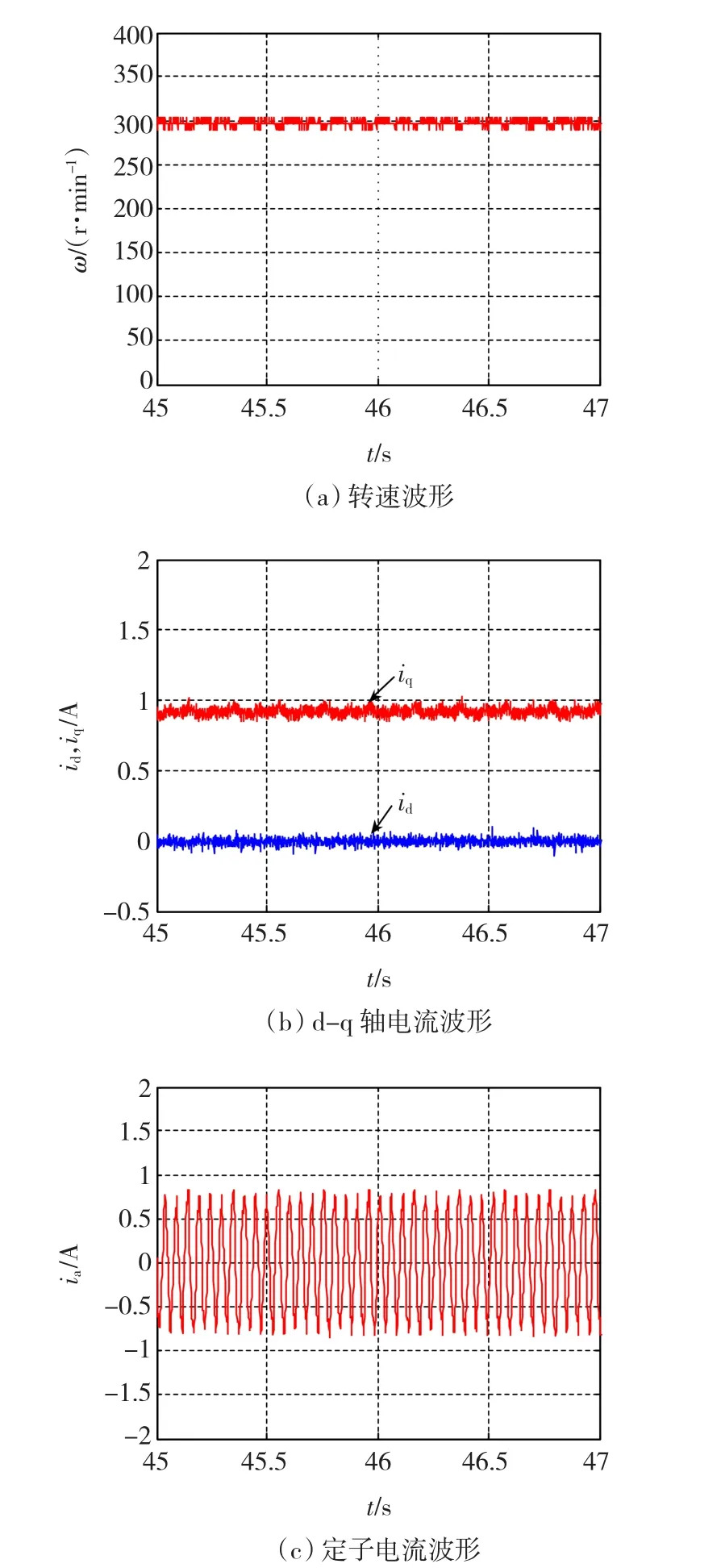
图5 反演控制系统的实验波形Fig．5 Waveform of backstepping control

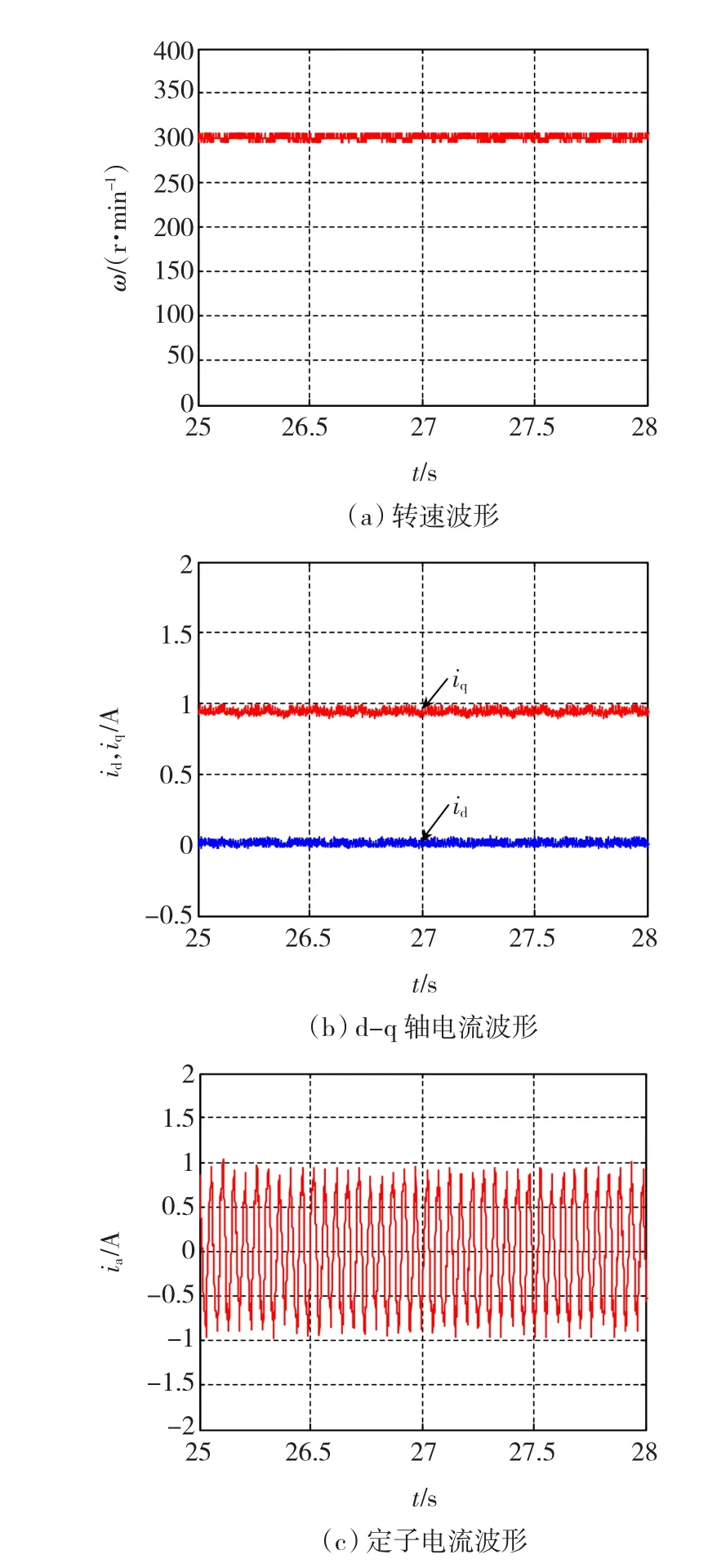
图6 积分滑模反演控制系统的实验波形Fig．6 Waveform of integral SM backstepping control

5 结论

本文针对高空电推进系统用永磁同步电机反演控制系统在电机稳态运行时存在转速静态误差以及易受系统参数影响的问题，提出了一种基于反演的积分滑模控制算法。该算法采用误差积分因子对转速进行动态补偿，通过指数趋近律构造d－q轴电流误差的滑模面方程来降低控制系统对参数摄动的敏感性。通过研究得出以下结论:

1)转速误差积分因子能够对转速进行动态补偿，当电机稳态运行时PMSM积分滑模反演控制系统在干扰条件下不存在转速静态误差。

2)利用指数趋近律构造d－q轴电流误差的滑模面方程的方法能够提高反演控制系统的转速动态响应，增强系统的鲁棒性。仿真和实验结果表明，相比于反演控制，参考转速突增时，积分滑模反演控制系统的转速动态响应时间由0.2 s减小到0.1 s，由负载转矩突变引起的转速超调由8 r/min减小到2 r/min，能够实现快速鲁棒自适应控制。

该控制策略简单易行，能够应用于各种电推进系统用PMSM的控制系统设计。同时，本文给出的系统参数摄动条件有限，在该条件下并未出现转矩脉动及抖振等现象，而在高空环境中系统参数摄动对控制系统性能的影响需要进一步深入研究。

［1］ 罗玲，刘卫国，窦满峰，等．高空飞艇螺旋桨驱动电机分析［J］．宇航学报，2009，30(6):2140－2144．LUO Ling，LIU Weiguo，DOU Manfeng，et al．Analysis of the motor driving a propeller of high altitude airship［J］．Journal of Astronautics，2009，30(6):2140 －2144．

［2］ 施红，宋保银，周雷，等．平流层飞艇的控制模式对其定点特性的影响［J］．航空学报，2009，30(5):800－805．SHI Hong，SONG Baoyin，ZHOU Lei，et al．Effect of the control style of a stratospheric airship on its floating performance［J］．Acta Aeronautica et Astronautica Sinica，2009，30(5):800－805．

［3］ 杨秉，杨健．临近空间飞艇运行环境及其影响［J］．航天器环境工程，2008，25(6):555－559．YANG Bing，YANG Jian．The operating environment of nearspace and its effects on the airship［J］．Spacecraft Environment Engineering，2008，25(6):555－559．

［4］ 杨喜军，蒋婷，佘焱．最优最小开关损耗SVPWM地板水暖变频调速系统［J］．电机与控制学报，2011，15(5):25－32．YANG Xijun，JIANG Ting，SHE Yan．Floor water-heating variable frequency speed control system using optimized minimized switching loss SVPWM ［J］．Electric Machines and Control，2011，15(5):25－32．

［5］ 王家军，赵光宙，齐冬莲．反推式控制在永磁同步电动机速度跟踪控制中的应用［J］．中国电机工程学报，2004，24(8):95－98．WANG Jiajun，ZHAO Guangzhou，QI Donglian．Speed tracking control of permanent magnet synchronous motor with backstepping［J］．Proceedings of the CSEE，2004，24(8):95－98．

［6］ LEU V Q，CHOI H H，JUNG J W．Fuzzy sliding mode speed controller for PM synchronous motors with a load torque observer［J］．IEEE Transactions on Power Electronics，2012，27(3):1530－1539．

［7］ 汪海波，周波．永磁同步电机调速系统的滑模控制［J］．电工技术学报，2009，24(9):71－77．WANG Haibo，ZHOU Bo．A PMSM sliding mode control system based on exponential reaching law ［J］．Transactions of China Electrotechnical Society，2009，24(9):71－77．

［8］ 郑剑飞，冯勇．永磁同步电机的高阶终端滑模控制方法［J］．控制理论与应用，2009，26(6):697－700．ZHENG Jianfei，FENG Yong．High-order terminal sliding-mode control for permanent magnet synchronous motor［J］．Control Theory＆ Applications，2009，26(6):697－700．

［9］ 刘治钢，王军政．永磁同步电机神经网络自适应滑模控制器设计［J］．电机与控制学报，2009，13(2):290－295．LIU Zhigang，WANG Junzheng．Neural network adaptive sliding mode control for permanent magnet synchronous motor［J］．Electric Machines and Control，2009，13(2):290 －295．

［10］ 王礼鹏，张化光，刘秀翀，等．基于扩张状态观测器的SPMSM调速系统的滑模变结构反步控制［J］．控制与决策，2011，26(4):553 －557．WANG Lipeng，ZHANG Huaguang，LIU Xiuchong，et al．Backstepping controller based on sliding mode variable structure for speed control of SPMSM with extended state observer［J］．Control and Decision，2011，26(4):553－557．

［11］ TAN Yaolong，CHANG Jie，TAN Hualin，et al．Integral backstepping control and experimental implementation for motion system［C］//IEEE Conference on Control Applications-Proceedings，September 25 － 27，2000，Anchorage，USA．2000，1:367－372．

［12］ LIU Jinkun，SUN Fuchun．Nominal model-based sliding mode control with backstepping for 3-axis flight table［J］．Chinese Journal of Aeronautics，2006，19(1):65 －71．

［13］ OUASSAID M，CHERKAOUI M，MAAROUFI M．Improved nonlinear velocity tracking control for synchronous motor drive using backstepping design strategy［C］//2005 IEEE Russia Power Tech，June 27 － 30，2005，St．Petersburg，Russia．2005:4524565．

［14］ CHANG S H，CHEN P Y．Robust current control-based sliding mode control with simple uncertainties estimation in permanent magnet synchronous motor drive systems［J］．IET Electric Power Applications，2010，4(6):441 －450．

［15］ ZHANG Yongpeng，CAJETAN M A．Load disturbance resistance speed controller design for PMSM［J］．IEEE Transactions on Industrial Electronics，2006，53(4):1198 －1208．