盘式永磁Halbach悬浮装置的磁场和力特性分析

秦伟， 范瑜， 马育华， 吕刚， 李硕， 朱熙， 刘国瑞

(1．北京交通大学电气工程学院，北京100044;2．中国煤炭科工集团太原研究院，山西 太原030006;3．山西运城供电分公司，山西运城044000)

0 引言

美国劳伦斯伯克利国家实验室的Halbach教授提出了Halbach永磁阵列的概念，并在20世纪90年代被国内外研究机构相继成功应用于新一代的粒子加速器、自由电子激光装置、同步辐射装置等高能物理领域中［1］。

国内外的专家学者提出将Halbach永磁阵列应用在磁悬浮电机中［1-3］，由于磁悬浮电机无机械接触，具有无污染，噪声小，容易维护，可靠性高的优点，在交通运输，特种电机，机器人，金属加工等很多场合得到了应用。

盘式永磁Halbach悬浮装置通过轴向运动的永磁体与导体板产生相对运动，在导体板中感应出涡流，涡流磁场与永磁体相互作用实现悬浮和导向。相对于电磁式的磁悬浮更有独到之处，即结构简单，悬浮气隙大，造价低，同时并不需要复杂的闭环控制，因此将是磁悬浮发展的重要方向［4-5］。

从导体板涡流分布的研究出发，在总结前人相关研究成果的基础上，完全使用解析方法，通过数学推导和分析，建立悬浮装置的分环电磁模型。采用行波磁场理论方法进行磁场分布求解，得出悬浮装置电磁部分的磁场表达式。对于横向边缘效应，将次级导体板的电导率进行修正;进而得出考量悬浮质量的悬浮力的表达式和水平转矩的表达式;通过有限元计算和样机实验来验证解析方法的正确性。

1 DHPMD的电磁模型

1.1 模型电机的分环电磁模型

图1为盘式永磁Halbch悬浮装置示意图。

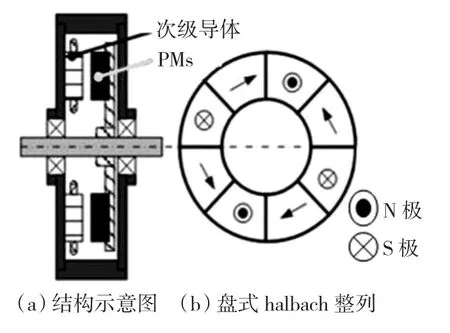
图1 盘式永磁Halbach悬浮装置Fig．1 DHPMD machines

由于盘式Halbach阵列主要参数随半径变化，采用平均直径法计算会造成较大误差［6］。因此本文建立基于分环计算方法的电磁模型，将盘式Halbach阵列沿径向等分为如图2(a)所示的n个环，将每个环沿径向剖开拉直，如图2(b)所示。将气隙磁场的径向分布转化为横向分布，各条状结构的主要参数分别与极距相关联，采用各环的平均极距计算;假设Halbach阵列纵向长度无穷大，以避免模型纵向开断对计算结果造成影响。这样就得到一组长度、宽度、高度一致的窄长直线电机结构。

图2 盘式Halbach阵列分环示意图Fig．2 Sub-loop model of ring arranged Halbach PMs

1.2 电机电磁场分析

为了计算电机的磁场和力特性，首先对模型作一下假设［6-7］:

1)气隙磁场强度沿z轴是恒定的值;

2)永磁体沿x轴运动，导体板中的感应电流只有z轴分量;

3)各层的物理参数是均匀的，各向同性的。

基于以上假设建立如图3所示的坐标系。图3为任意一环沿径向切开拉直后的展开图，区域1为Halbach永磁体区域，区域4为次级导体，采用铝材料，区域2，区域3和区域5均为气隙。假设悬浮装置结构对称，在运动方向上闭合，故不存在类似直线电机的纵向边端效应问题，但由于受极距影响的各电磁场量随半径增大变化明显，横向边端效应的影响较为突出，在气隙较大时会造成10%以上的误差，横向边缘效应导致的结果是损耗的增加，较好的方法是修正次级导电率和阻抗［7］。经过修正的次级电导率σ'=kALσ，其中，σ为导体板实际电导率，kAL为修正系数，kAL=1-tanh(ka)/{ka［1+tanh(ka)tanh(kl-ka)］}，k=π/τ，τ为极距，a 为初级永磁体宽度的1/2，l为次级导体板宽度的1/2。

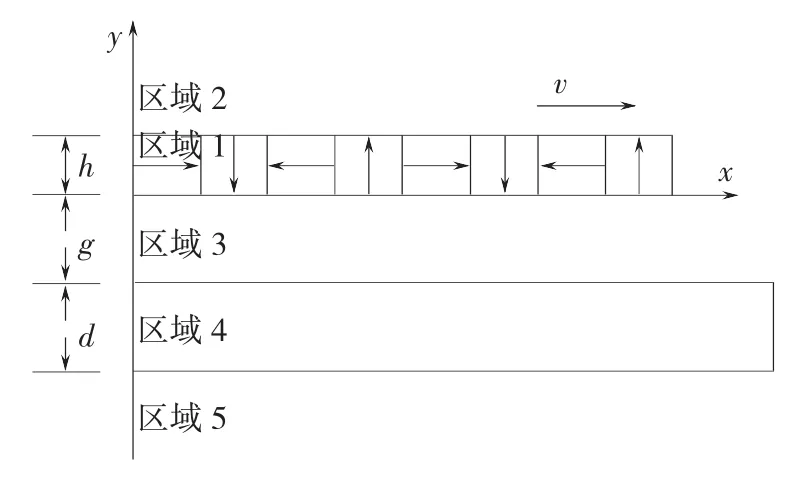
图3 侧面展开图与求解坐标系Fig．3 Side elevation and coordinate system

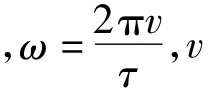
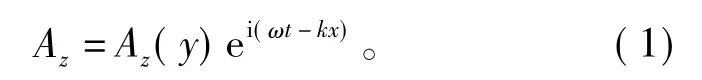
a)Halbach阵列磁场分析

永磁体和导体板之间的相对速度v=0时，在导体板中不能感应出涡流，可以认为导体板的相对磁导率与空气近似相等，则图3中区域3，区域4，区域5可认为是一个气隙区域，此时图3中求解区域可等效为如图4所示的求解坐标系。

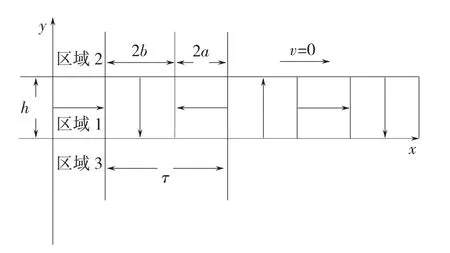
图4 v=0时的求解坐标系Fig．4 Coordinate system at v=0

将间断的永磁体等效成一个连续的永磁体面，对于每一块永磁体［6，8］有

B= μ0(H+M)=μ0(μ'rH+M0)。

式中:B为磁感应强度;H为磁场强度;μ0为真空中的磁导率;μ'r为永磁体的相对磁导率;M0为剩余磁化强度，为常数，其表达式为

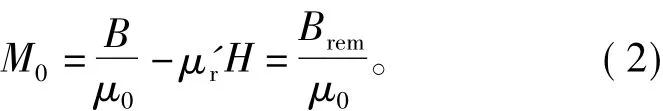
式中Brem为剩余磁感应强度。

根据拉普拉斯变化，可得到等效之后的连续永磁体沿y轴方向的剩余磁化强度My，沿x轴方向的剩余磁化强度Mx，即

My=-4M0/(qπ)sin(qπ/τ)，

Mx=i8M0/(qπ)sin［qπa/(2τ)］sin［qπ(a+2b)/(2τ })］。

式中:a为沿x轴方向充磁永磁体宽度的1/2;b为沿y轴方向充磁永磁体宽度的1/2;q为奇数。

图4中各区域的磁矢量函数Az如式(3)～式(5)所示。

区域1 (永磁体)的磁矢量函数为

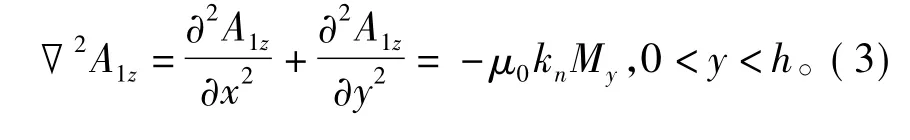
由式(13)，式(14)和有限元计算可以得到不同气隙下的磁场分布，如图5和图6所示。

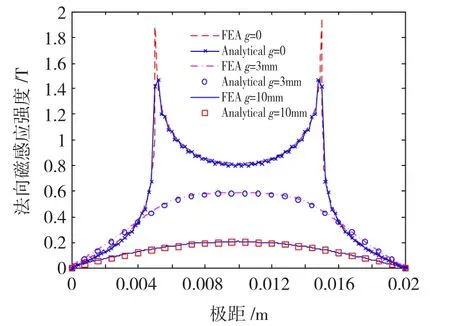
图5 气隙为0，3，10 mm时Halbach阵列磁力线分布图Fig．5 2－d flux distribution of Halbach array when air-gap are 0，5，10 mm

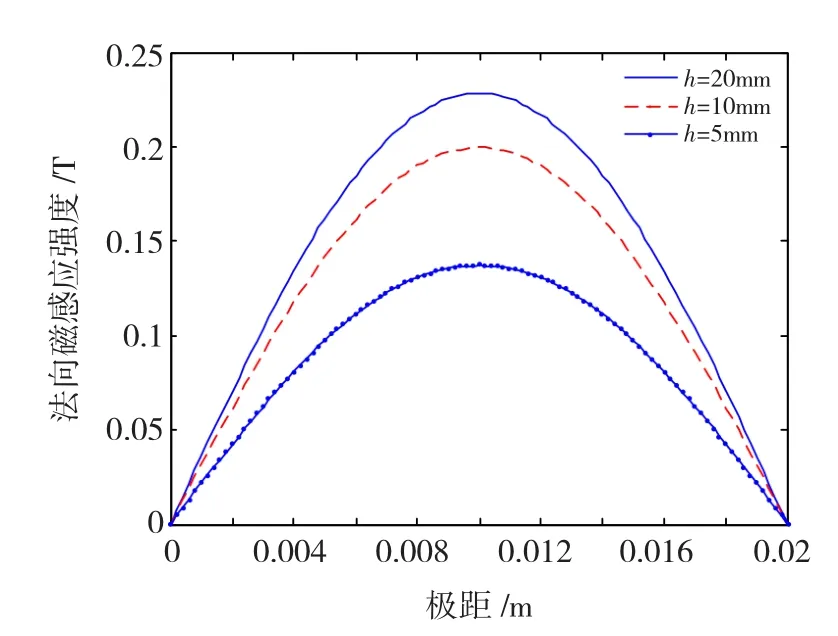
图6 永磁体厚度为5，10，20 mm时Halbach阵列磁力线分布图Fig．6 2-d flux distribution of Halbach array when thickness are 5，10，20 mm

整理和对比解析计算和有限元计算的结果可以得到如下结论:1)从图5中可以看出，解析法和有限元法两种方法拟合得较好，证明本文的解析方法是有效的，正确的;2)从图6中可以看出，随着永磁体厚度的增加气隙磁场逐渐增大，并且随着厚度的增加磁场的增加量逐渐减少，因此要选择合适的永磁体厚度。

b)电机的磁场和动态特性分析

当永磁体和导体板的相对速度v≠0时，在导体板中将感应出涡流，永磁体与涡流磁场相互作用产生悬浮力和转矩。图3中各区域的磁矢量函数Az［9-15］如式(15) ～ 式(19)所示。

2 实验验证与理论计算

2.1 悬浮力特性

样机次级导体板固定，其悬浮力Flift可采用麦克斯韦张量定理计算［16］，即

根据磁场分布的解析表达式和式(29)可以求得悬浮力Flift与永磁体转速、厚度，以及气隙长度等参数之间的关系。

图7为永磁体厚度为10 mm，不同气隙条件下，悬浮力随永磁体速度变化的情况，从图7中可以看出，随着转速的增加悬浮力逐渐增加，但随着转速上升至15 r/s左右之后，悬浮力随永磁体转速的增加变化并不明显，故该装置在应用中应综合考虑，选择合适的速度范围。

图8为在转速为50 r/s，气隙长度为10 mm条件下，悬浮力和永磁体厚度的关系。由图8可知，悬浮力随永磁体厚度的增长逐渐上升，但当永磁体厚度增加到0．02 m后悬浮力将趋于饱和，这是由于随着永磁体厚度增加到一定程度，导体板的损耗增加，因此要选择合适的永磁体厚度。

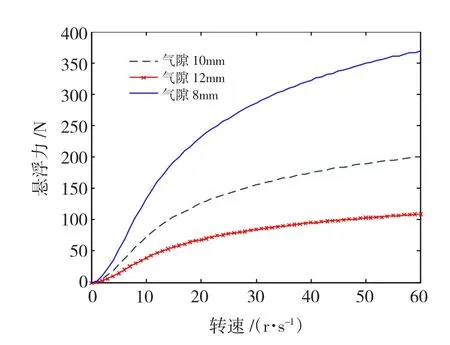
图7 悬浮力与速度关系曲线Fig．7 Curve between lift force and velocity

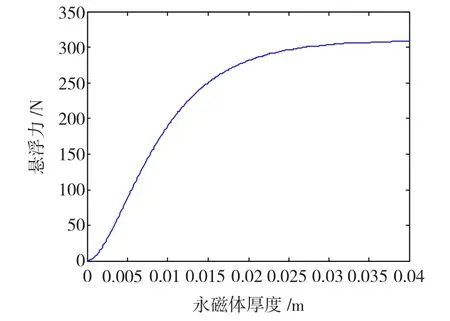
图8 悬浮力与永磁体厚度关系曲线Fig．8 Curve between lift force and thickness of PMs

图9为在其他参数不变的情况下，悬浮力和重力之比与永磁体厚度的关系，随着永磁体厚度的增加悬浮增加，但是永磁体的重量也在增加。由图9可知，在其他参数不变的情况下，悬浮力和永磁体重力之比在永磁体厚度为0．008～0．01 m时达到最大，因此永磁体最佳厚度为0．008～0．01 m。

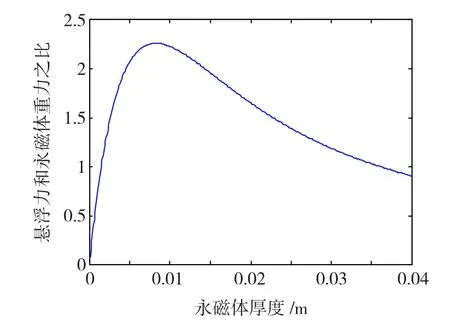
图9 悬浮力和永磁体重力之比与永磁体厚度的关系Fig．9 Curve between lift force divided by permanent weight force and thickness of PMs

图10为在转速为50 r/s，永磁体厚度为10 mm条件下，悬浮力随气隙长度变化的情况(图中点划曲线为理论计算结果，▽表示有限元计算结果，o表示实验测得的结果经过数据处理后得到的平均值)。由于拉/压力传感器在低量程范围内及被检测力在拉力、压力间转换时存在一定的误差，会使测量值偏小;计算过程中忽略了高次谐波等次要因素的影响，会使计算值小于实际值，实验测量结果和计算结果存在一定的差距，但三者变化趋势相同。

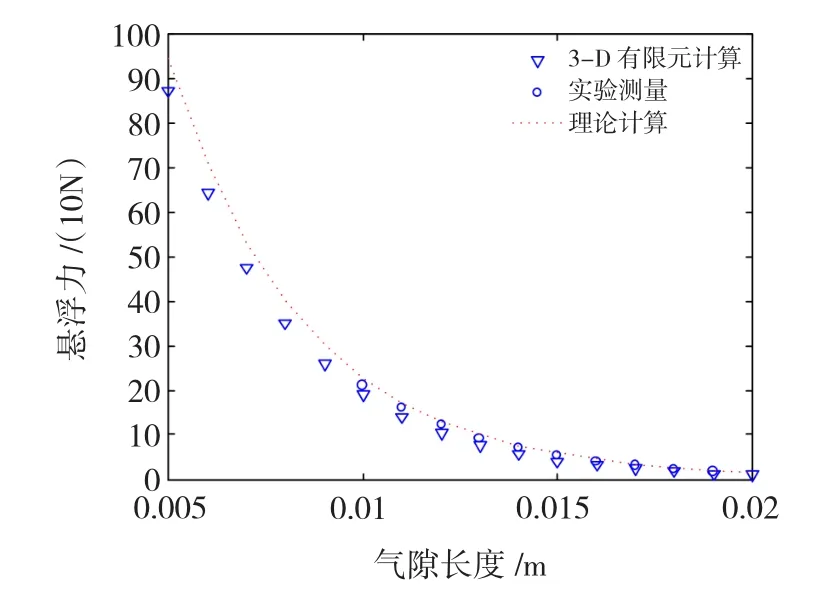
图10 悬浮力与气隙长度关系曲线Fig．10 Curve between lift force and air-gap length

2.2 转矩特性

本文提出的悬浮装置在产生竖直方向上的悬浮力的同时也存在水平转矩，水平转矩会造成悬浮装置和搭载车辆的连接部位产生机械扭力，危害连接处的可靠性。所以水平转矩在悬浮装置中是危害装置结构和运行稳定的无用力，应采取措施予以限制。在实际应用中，可以成对使用气隙磁场互为反向转动的装置，产生大小相等，方向相反的转矩来抵消初级水平转矩对搭载车辆的影响，但这也需要对装置的水平转矩准确估算和控制。图11为在永磁体厚度为10 mm，不同气隙长度条件下，悬浮力随永磁体速度变化的情况。由图11可知，装置的水平转矩特性曲线形式与柱状感应电机类似，可通过对次级优化设计来改变次级电阻，选择合适的工作点，使相同悬浮力条件下的水平转矩最小。

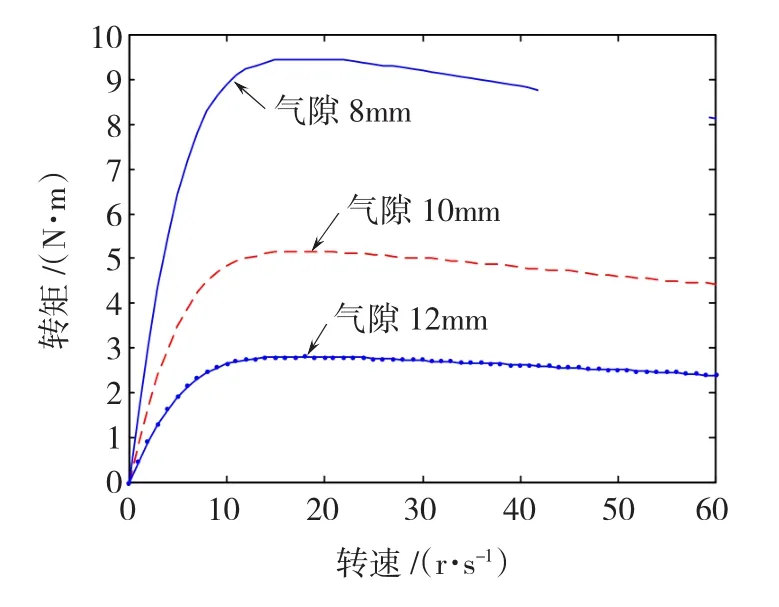
图11 不同气隙长度下水平转矩与转速关系曲线Fig．11 Curve between torque and velocity of the different air-gap length

图12为在气隙长度为10 mm，转速为50 r/s条件下，水平转矩与永磁体厚度的关系。由图12可知，水平转矩也随永磁体厚度增大而逐渐增加，说明永磁体厚度对悬浮力和水平转矩的贡献方式是相同的［16］。

图12 水平转矩与永磁体厚度关系曲线Fig．12 Curve between torque and and thickness of PMs

3 结论

本文采用完全解析法建立数学模型，通过Ansoft有限元软件建立有限元模型，计算盘式永磁Halbach悬浮装置的磁场和力特性结果，并通过样机实验对计算结果进行了验证，主要结论为:

1)本文采用完全解析法构造的分环电磁模型考虑了悬浮装置各参数随半径变化的因素，对悬浮装置的力特性和转矩进行了分析计算，解析计算结果与有限元计算、实验结果基本吻合。

2)随着永磁体厚度和Halbach永磁体结构电动机的气隙磁场的逐渐增加，悬浮力、转矩增加较快，水平转矩的增加会造成悬浮装置的不可靠，因此需要选择合适的参数使悬浮装置在稳定悬浮的情况下尽量减少水平转矩，其中最有效的方法是旋转的永磁体成对使用，但运动方向相反。

［1］ 王厚生．永磁电动式导体板磁悬浮列车轨道结构及相关研究［D］．北京:中国科学院电工研究所，2004．

［2］ BIRD J，LIPO T A．Calculating the forces created by an electrodynamic wheel using a 2-D steady-state finite-element method［J］．IEEE transactions on magnets，2008，44(3):365-372．

［3］ BIRD Jonathan．Thesis an investigation into the use of electro-dynamic wheels for high speed ground transportation［D］．University of Wisconsin，2007．

［4］ YAN Luguang．Development and application of the magnet technology in China［C］//Proceedings of Fifteenth International Conference on Magnet Technology，October 20-24，1997，Beijing，China．1997:30-35．

［5］ CHOI J Y，PARK Y S，JANG S M．Magnetic field computation of axial flux permanent magnet machines with Halbach and axially magnetized rotor using quasi-3-D analysis modeling［C］//Digests of the 2010 14th Biennial IEEE Conference on Electromagnetic Field Computation，CEFC 2010，May 9-12，2010，Chicago，USA．2010:5480486．

［6］ WANG Housheng，YE Ying，WANG Qiuliang，et al．Analysis for ring arranged axial field Halbach permanent magnets［J］．IEEE Transactions on Applied Superconductivity，2006，16(2):1562-1565．

［7］ ANASAR S．Linear motion electric machines［M］．New York:A Wilcy-Interscience Publication，1976:57-137．

［8］ 李春生，杜玉梅，夏平畴，等．直线型Halbach磁体和导体板构成的电动式磁悬浮系统的分析及实验［J］．电工技术学报，2009，24(1):18-22．LI Chunsheng，DU Yumei，XIA Pingchou，et al．Analysis and experimental testing of eds maglev with linear Halbach and conducting sheet［J］．Transactions of China Electro-technical Society，2009，24(1):18-22．

［9］ LEQUESNE B，LIU Buyun，NEHL T W．Eddy current machines with permanent magnets and solid rotors［J］．IEEE Transactions on Industry Applications，1997，33(5):1289-1294．

［10］ NEHL T W，LEQUESNE B，GANGLA V，et al．Nonlinear two-dimensional finite element modeling of permanent magnet eddy current couplings and brakes［J］．IEEE Transactions on Magnetics，1994，30(5):3000-3003．

［11］ 辜承林．次级无铁心式直流永磁盘式电机的磁场和解析解分析与优化设计［J］．中国电机工程学报，1996，16(2):125-129．GU Chenglin．Optimization of permanent-magnet axial field coreless DC motors based on magnetic-field-magnet method［J］．Proceedings of the CSEE，1996，16(2):125-129．

［12］ 唐孝镐，宁玉泉，傅丰礼．实心转子异步电机及其应用［M］．北京:机械工业出版社，1991:1-191．

［13］ GASTLI A．Compensation for the effect of joints in the rotor conductors of a linear induction motor［J］．IEEE Transactions on Energy Conversion，1998，23(2):111-116．

［14］ 唐永春．超导磁浮直线电机及其控制和涡流制动系统研究［D］．浙江:浙江大学电气工程学院，2006．

［15］ EDWARD J D，JAYAWANT B V，DAWSON W R C，et al．Permanent magnet linear eddy-current brake with a nonmagnetic reaction plate［J］．IEE Proceedings-Electric Power Applications，1999，146(6):627-631．

［16］ 朱熙，范瑜，吕刚，等．单边盘式感应电机的数学模型与转矩分析［J］．中国电机工程学报，2010，30(24):69-74．ZHU Xi，FAN Yu，LÜ Gang，et al．Modeling and torque analysis of a disc induction motro［J］．Proceedings of the CSEE，2010，30(24):69-74．