状态切换UKF的飞行器姿态确定算法

吴勃， 徐欢， 乔相伟

(1．哈尔滨理工大学自动化学院，黑龙江哈尔滨 150080;2．北京环球信息应用开发中心，北京 100094;3．西安航天精密机电研究所系统工程事业部，陕西西安 710100)

0 引言

飞行器姿态确定是飞行器控制系统的关键组成部分。常用的姿态描述参数有方向余弦矩阵、欧拉角、姿态四元数(quaternion)、罗德里格参数(rodrigues parameters，RPs)、修正罗德里格参数(modi-fied rodrigues parameters，MRPs)、凯莱 － 哈密尔顿参数［1］等。其中姿态四元数因为计算量小、非奇异性、可全姿态工作而广泛应用于实际系统当中［2－3］。但由于四元数的4个参数存在冗余，4个变量并不独立，使他必须满足规范化限制。如何克服四元数的规范化限制，让他与先进的滤波算法相结合成为目前国内外研究的热点问题［3］。

目前最常用的飞行器姿态确定算法是状态估计算法。然而该算法将不可避免地要涉及到非线性滤波问题。而基于泰勒展开的扩展卡尔曼滤波［4］(extended Kalman filter，EKF)，其本质是 Kalman滤波在非线性系统中的推广，该算法比较简单，只达到了对非线性系统的一阶估计精确度。针对此，之后的学者又提出了二阶EKF算法［5］，滤波精确度得到较大提高，但是因为该算法涉及到Hassian矩阵的计算，使得计算负担也大为增加，实际应用反而没有EKF广泛。考虑到对非线性函数后验均值和方差的近似远比对非线性函数本身的近似简单，近年来，Julier等提出了无迹卡尔曼滤波算法［6］。该算法首先以系统状态的先验均值和方差为基准，选取一组确定性采样点，称为Sigma点，使得这组采样点的统计特性与状态先验统计特性相一致，然后将利用系统非线性传递函数得到一组新的采样点，最后采用加权统计线性回归技术得到这组样本点的统计特性，作为非线性函数的后验统计分布。然而早期的无迹卡尔曼滤波(unscented Kalman filter，UKF)算法并没有考虑系统噪声对滤波精确度和稳定性的影响。为此，武元新和M．Briers等从非线性系统噪声出发，分析了系统噪声对UKF算法的滤波性能的影响，指出忽略噪声的非线性传递特性的标准UKF算法会一定程度地降低滤波的精确度和稳定性，并从理论上给出了扩维UKF(augmented UKF，AUKF)算法可以提高滤波精确度的证明［7］。在此基础上，Merwe在2004年给出了3种形式的扩维UKF算法［8］，包括只将过程噪声或者量测噪声纳入扩维状态的单边扩维UKF算法和噪声全部纳入扩维状态的全维 UKF算法(all－dimensional UKF，AUKF)。其中全维UKF算法最为典型，应用也最广。该算法通过扩维将过程噪声和量测噪声全部纳入状态变量中参与Sigma点选取，提高了UT变换的后验逼近精确度，进而提高了滤波的精确度和稳定性。但该算法同时也带来了状态维数倍增，计算负担加重的问题。而事实上在多数情况下，系统的量测与过程是不相关的，即传感器的量测精确度并不受载体机动变化的影响。为此，提出一种过程和量测不相关的状态切换UKF滤波(state switching UKF，SSUKF)算法，并将其应用到飞行器姿态确定中去。针对姿态确定过程中四元数均值计算问题和协方差奇异性问题［9－11］，采取将四元数参数和修正罗德里格斯参数相结合的方法，即在均值和协方差计算时将四元数参数切换为修正罗德里格斯参数，而在状态传递时采取四元数形式，这样既避免了修正罗德里格斯参数积分带来的高计算复杂度问题，又解决了四元数的规范化问题。针对大姿态误差角的SINS/CCD飞行器姿态仿真结果表明，该算法与全维UKF算法相比，估计精确度相当，但估计时间缩短了约1/3。

1 飞行器姿态确定状态空间模型

1.1 飞行器状态空间模型

本文以飞行器姿态参数和陀螺漂移为状态变量，建立飞行器姿态确定系统状态方程，其微分形式为

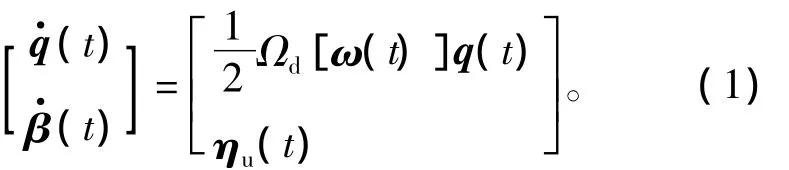
式中:Ωd［ω(t)］为姿态更新函数;q(t)为姿态四元数;ω(t)=(t)－β(t)－ηv(t);(t)为角速度量测值;β(t)为一阶马尔科夫过程;ηv(t)，ηu(t)均为零均值白噪声。

以星敏感器四元数输出作为量测输出，则姿态确定系统测量数学模型为

式中:q为真实姿态四元数;qn为星敏感器测量噪声的四元数表示形式。

1.2 飞行器姿态动力学方程

以近地卫星为例，建立飞行器姿态动力学方程［12］为

式中:J为飞行器本体的转动惯量;hw为飞行器内部运动部件的总动量;Tc为控制力矩;Td为干扰力矩。

2 状态切换UKF算法

2.1 全维UKF算法

考虑如下非线性离散系统，即

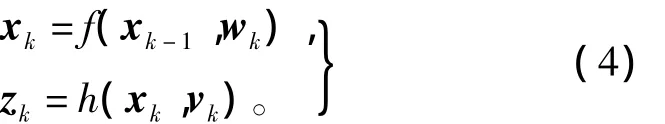
式中:xk∈Rn为k时刻的系统状态向量;zk∈Rm为k时刻的系统量观测向量;ωk∈Rn，vk∈Rm分别为服从N(0，Q)和N(0，R)分布的高斯白噪声。

选取扩维系统状态变量xa=［xTwTvT］T。其中，x，w，v分别为系统状态变量，过程噪声变量和量测噪声变量。

1)初始化

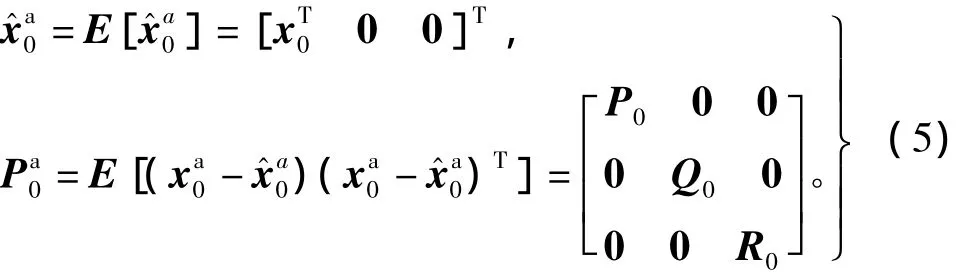
式中:x0为系统状态初始值;P0，Q0，R0分别为系统状态初始误差方差阵，过程噪声初始误差方差阵和量测噪声初始误差方差阵。

2)时间更新

时间更新阶段Sigma点及权值选取为

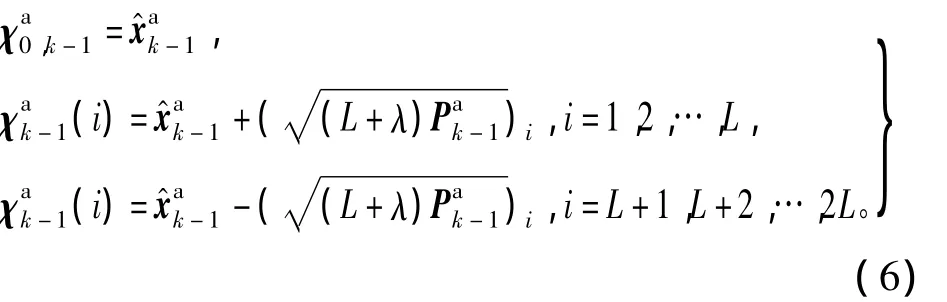
上述Sigma点对应的均值权值和方差权值分别为

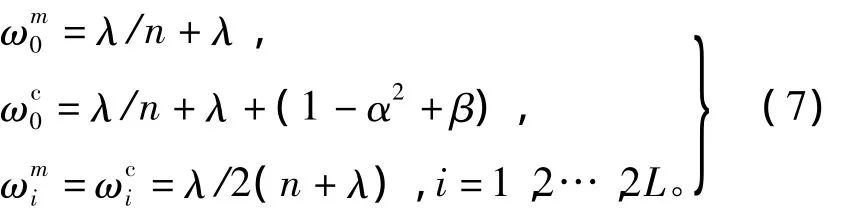
式中:L=2n+m;λ=α2(n+κ)－n为尺度因子，α决定了这些Sigma点集到均值点的距离，通常设置为一个很小的正数，κ通常设置为零;β用于融入随机变量的验前信息［8］。

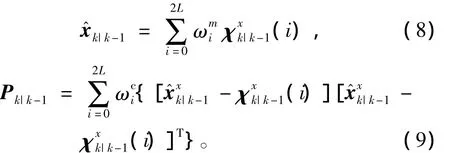
3)量测更新

量测更新阶段Sigma点选取为

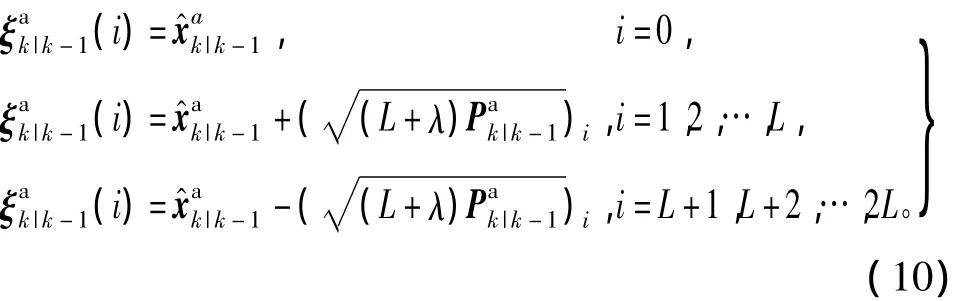
通过非线性量测函数 Zk|k－1(i)=］，可得k时刻系统量测一步预测均值，方差及互协方差分别为

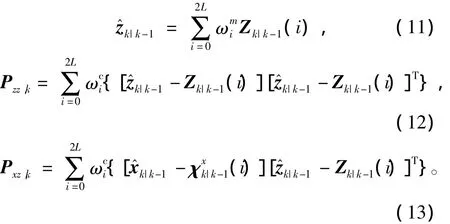
4)状态更新

由上式可得系统状态增益矩阵，估计值及状态误差方差值分别为

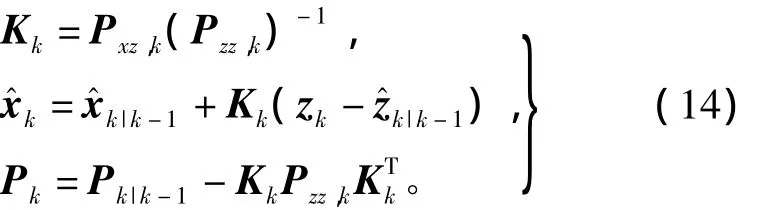
由扩维UKF算法可知，量测噪声参与了时间更新过程，而过程噪声也参与了量测更新过程。而在实际系统中，大多数情况下量测与过程是不相关的。此时，量测噪声在时间更新过程中只是单纯地增加了滤波的计算量，对状态预测更新起不到太大作用，另外由整个滤波过程可知，噪声向量并没有得到更新。这是因为系统假设的噪声为零均值高斯白噪声，所以噪声的最优估计值为零，只需要在每次滤波开始前赋值为零即可。

2.2 状态切换UKF算法

由扩维UKF算法可知，通过扩维状态维数由n维增加为2n+m维，对应的Sigma点也由2n+1个增加到4n+2m+1个。这无疑将极大增加UKF算法的计算量。对此，本文提出一种过程与量测不相关的状态切换UKF算法。下面给出该算法的具体步骤。

1)初始化

选取扩维状态变量 xa=［xTwTvT］T。其中，x为待估计的系统状态向量，w和v分别为过程噪声向量和量测噪声向量。

扩维状态初始估计值和误差方差值如式(5)所示。

2)时间更新

时间更新过程因为观测噪声没有参与，选取扩维状态变量为状态向量和过程噪声。k时刻滤波状态变量及方差选取为

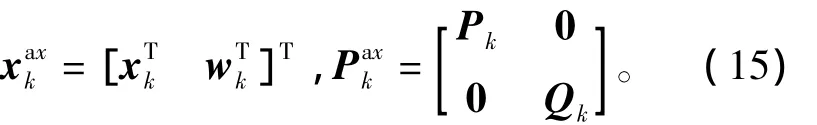
式中:xk，wk分别为k时刻的状态向量和过程噪声;Pk，Qk则分别为k时刻的状态向量和过程噪声对应的误差方差矩阵。

k时刻时间更新Sigma点选取为

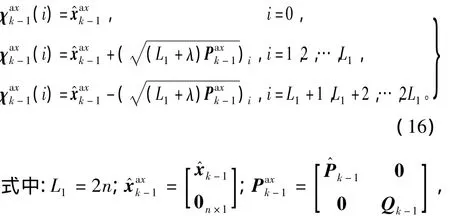
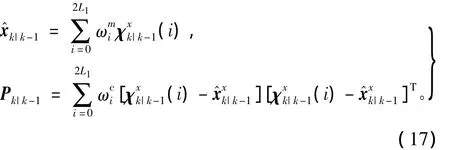
3)量测更新

量测更新过程中，由于过程噪声不参与更新，切换状态维数L2=n+m，此时扩维状态变量选取为状态向量和量测噪声，即

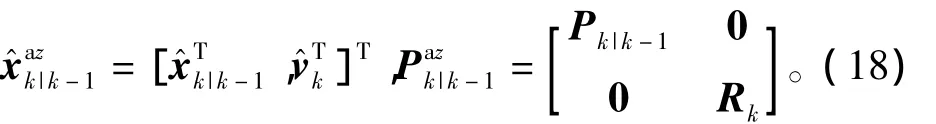
量测更新阶段Sigma点选取为

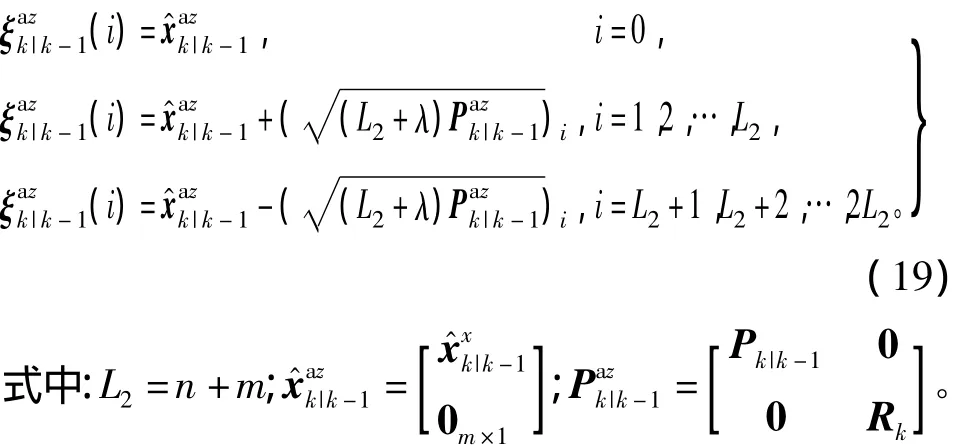
通过非线性量测函数 Zk|k－1(i)=h［(i)，］，其中，)分别为量测更新Sigma点的状态向量部分和量测噪声部分，可得k时刻系统量测一步预测均值，方差及互协方差为

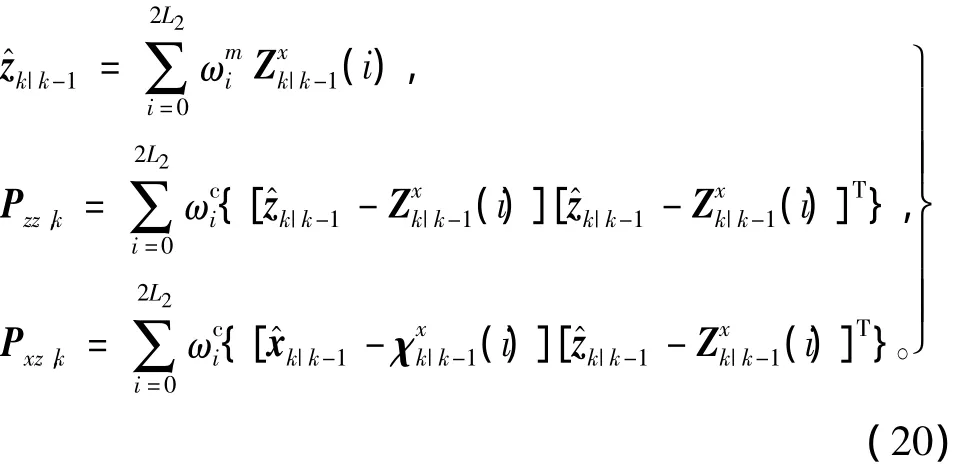
4)状态更新

状态更新与全维UKF相同，这里不再赘述。

由上面状态切换算法可知，在时间更新和量测更新滤波过程中状态维数分别由2n+m维减小为2n维和n+m维，对应的Sigma点分别由4n+2m+1个点减小为4n+1个点和2n+2m+1个点。状态维数的减小不仅影响了Sigma点选点的减少，而且在滤波时间更新和量测更新阶段也大大减小了计算量。在不影响滤波精确度的前提下，节省了滤波的时间，提高了系统的实时性。

3 飞行器姿态UKF算法

3.1 四元数规范化问题

相比于其他姿态描述参数，四元数因为计算量小、非奇异性和可全姿态工作成为姿态描述的首选。然而，四元数规范化要求却限制了其在非线性滤波中的应用。四元数规范化问题的核心是四元数加权均值计算问题，四元数加权均值¯qsimple最直接的方法［13］为

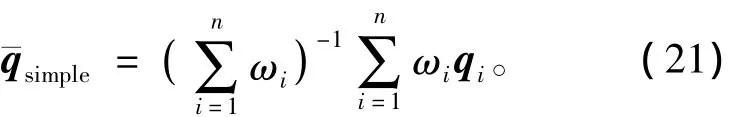
但是这样就会带来两个问题，其一，均值四元数¯qsimple将不再是一个规范的四元数;其二，q和－q表示相同的矢量旋转，也就是说改变四元数的符号并不应该影响四元数的加权均值，但是由式(21)所得的均值四元数显然不能满足这一点。

解决四元数规范化问题的一个方法就是姿态参数切换算法，具体来讲就是在涉及四元数均值及协方差计算时，将四元数通过姿态参数切换转化为3参数的MRPs，利用MRPs进行均值及协方差计算就避免了四元数协方差的奇异性问题。用四元数表示的MRPs参数为

式中:g为MRPs参数;a，b均为标量;ρ为四元数的向量部分;q4为四元数标量部分。

用MRPs表示的四元数参数为

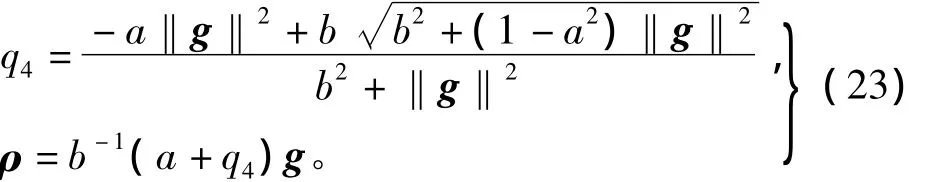
3.2 飞行器姿态UKF算法

本文在滤波过程中采取四元数和修正罗德里格斯参数实时切换的方法，有效解决了四元数的规范性问题。同时考虑到姿态确定中噪声非线性传递的特性，将前面的状态切换UKF算法应用到姿态确定中去。下面给出基于状态切换UKF的飞行器姿态确定算法的具体流程。

对于低年级孩子来说，作文评语有时可能被孩子忽略了，有时孩子还不是很懂老师的意思。所以，只写评语是不够的。每次习作我都坚持及时面批，让孩子看着老师改他的作文，具体地进行指导。面批，让孩子直观了解自己的作文，哪些地方这样写是好的，哪些地方怎样改会更好。要让孩子体会到老师的鼓励，老师对他作文的热情和重视。低年级学生的作文篇幅不长，老师若利用好零散的课余时间，是可以做到人人面批的。

选取扩维状态变量为 xa=［xT，wT，vT］T=［pT，其中 x=［pT，βT］T，w=［，p 为 MRPs形式的姿态变量，β 为陀螺漂移，ηv，ηu为过程噪声向量，ηs为量测噪声。

1)初始化

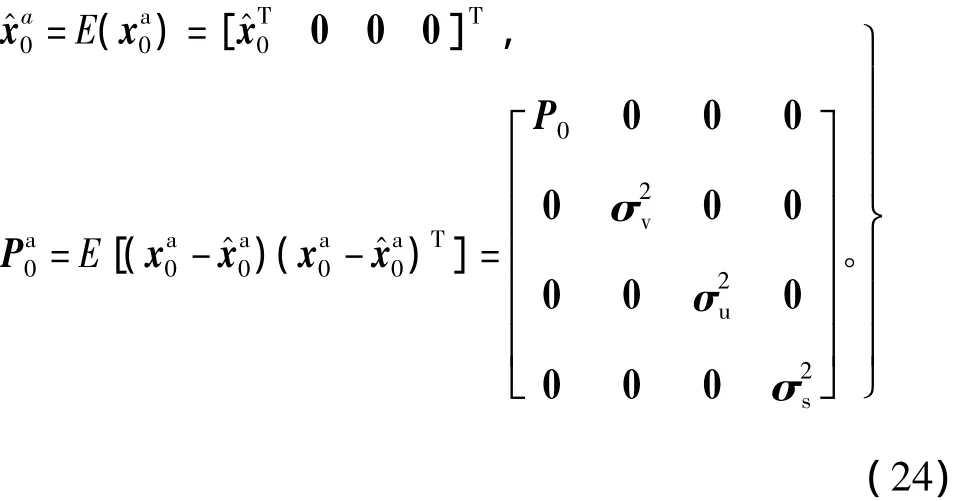
2)时间更新

时间更新阶段，没有量测噪声参与，此时扩维状态变量选为

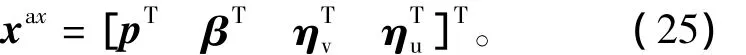
式中p为用修正罗德里格斯参数形式描述的飞行器姿态向量。

时间更新阶段Sigma点及权值选择，在已知k－1时刻状态分布的基础上，选取k时刻状态Sigma点为

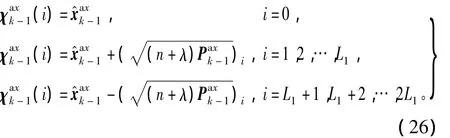
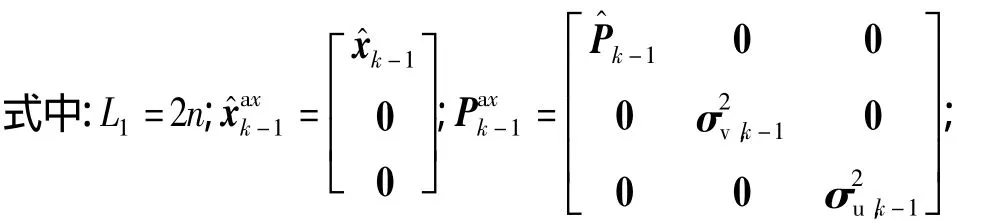
由于状态变量在时间更新时涉及到四元数更新，首先将上述Sigma点分为MRPs和非MRPs两部分，即

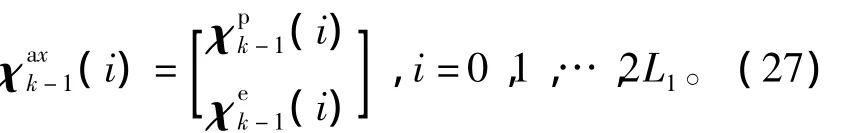
将MRPs参数点转换为四元数Sigma点，即

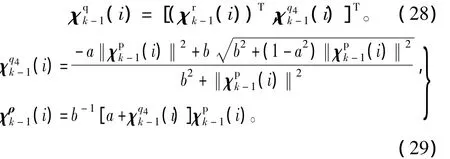
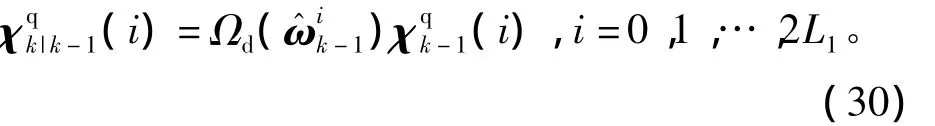
为了计算姿态预测均值需要将四元数一步预测值转换为MRPs形式的一步预测值，即

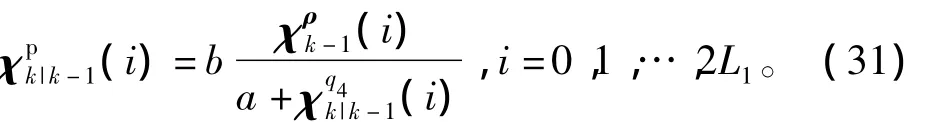
陀螺漂移的时间更新为

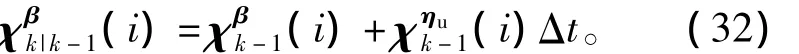
从而得到状态预测均值为

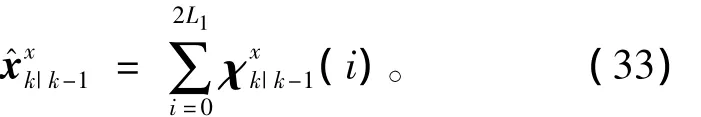
对应的状态预测误差方差值为

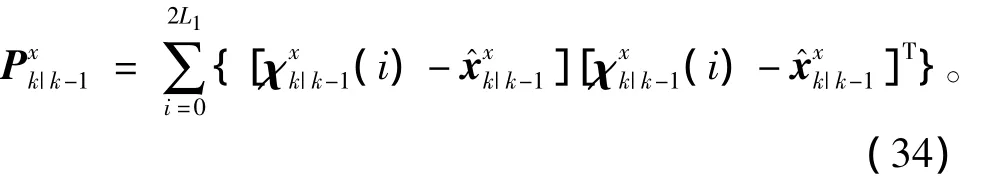
(3)量测更新

测量更新部分过程噪声未参与其中，切换扩维系统状态为

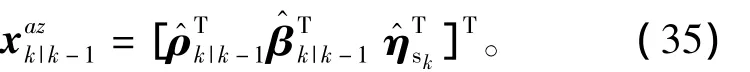
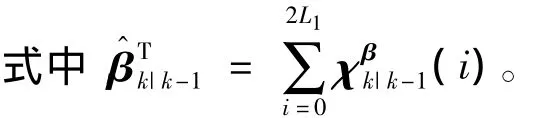
测量更新过程中Sigma点选取为

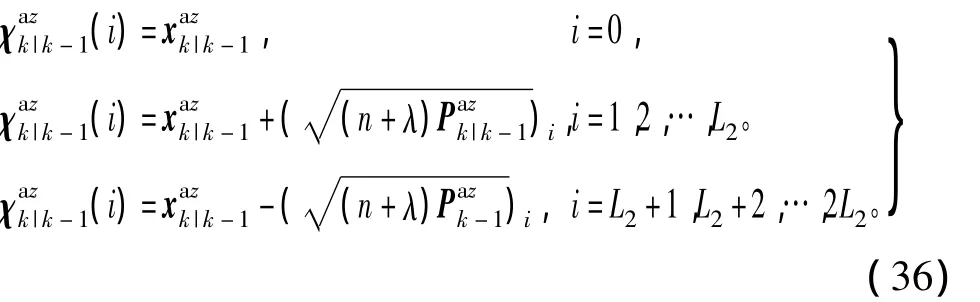
由于量测更新中只有姿态观测矢量，此时需要用四元数形式进行更新，首先将上述Sigma点分为MRPs部分和非MRPs部分，即

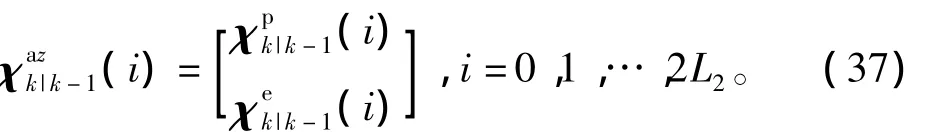
将MRPs点转换为四元数Sigma点，即

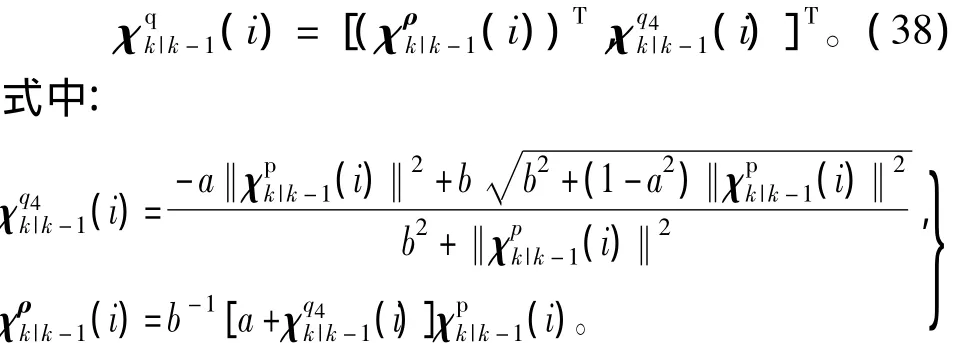
四元数量测一步预测值为

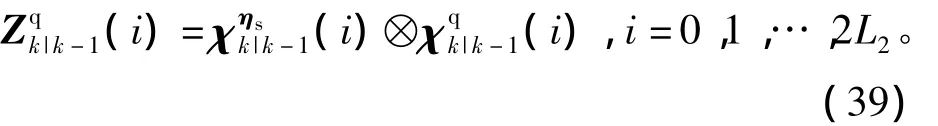
类似于时间更新，此时将四元数形式的姿态量测预测值转换为MRPs形式的姿态预测值，即

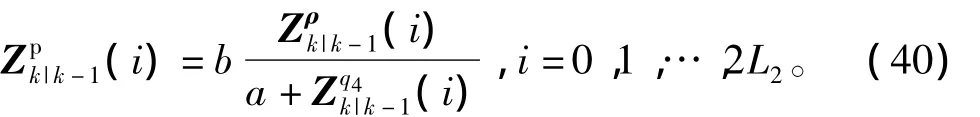
由于量测量中没有陀螺漂移，所以状态量测预测均值为

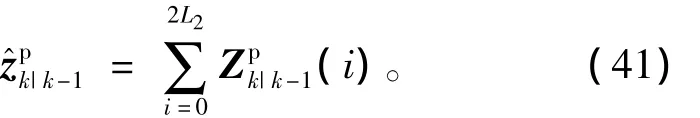
从而可得状态量测误差方差阵及互协方差值分别为

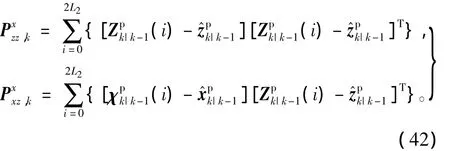
4)状态更新

状态增益矩阵更新为

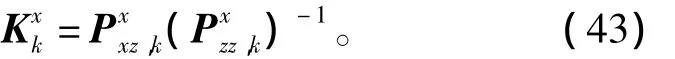
从而状态误差值及状态估计值分别更新为

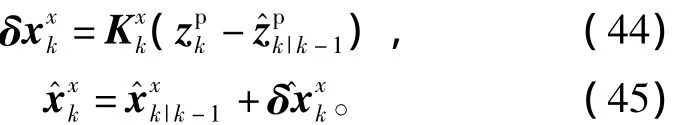
状态估计误差方差阵为

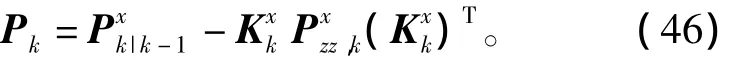
4 仿真实验研究

本文以近地卫星为例，建立SINS/CCD姿态估计系统仿真平台，为各种姿态确定算法提供统一的仿真实验平台，该系统软件开发语言主要是Matlab和C++。

1)飞行器参数设置

飞行器轨道为典型的近地圆轨道，轨道高度为800 km，倾角为60°，飞行器飞行轨道角速度 Ωo=0.001 rad/s，飞行器初始姿态角速度分别为0.01°/s，0.01°/s，0.05°/s。卫星三轴初始姿态角分别为 1°，2°，10°。飞行器的转动惯量矩阵为

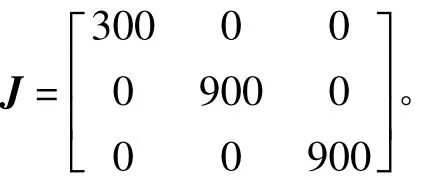
2)传感器参数设置

光纤陀螺测量白噪声为0.5°/h，驱动白噪声为0.02°/h，陀螺输出采样频率为100 Hz，星敏感器采用两个光轴垂直安装，其输出频率为4 Hz，飞行器初始姿态误差设定:横滚角，俯仰角，偏航角分别为1°，2°，10°。初始陀螺漂移在三轴上分别为 1°/h，1°/h，1°/h。星敏感器运动速率为 0.05°/s，测量白噪声标准差为20″，输出频率为4 Hz。卡尔曼滤波器中的姿态和陀螺漂移估计值均设定为零。

依据上述初始条件，分别采用全维UKF和状态切换UKF算法进行仿真，仿真结果如图1～图3和表1所示。

由图1和2可知，当初始姿态误差角较小取为1°和2°时，两种算法精确度相当且都以较快的速度收敛;而当初始姿态误差角为大角度时，由图3可知，两种算法在精确度相当的情况下，SUKF能以更快的速度收敛，收敛时间与AUKF相比。这是由于SUKF算法通过实时切换系统状态减小了状态的维数，降低了运算的复杂度。另外由表1平均一次迭代滤波所用时间也可以看出，SUKF算法与UKF算法相比滤波时间减少了大约1/3，这也再次验证了该算法在提高系统实时性方面的有效性。

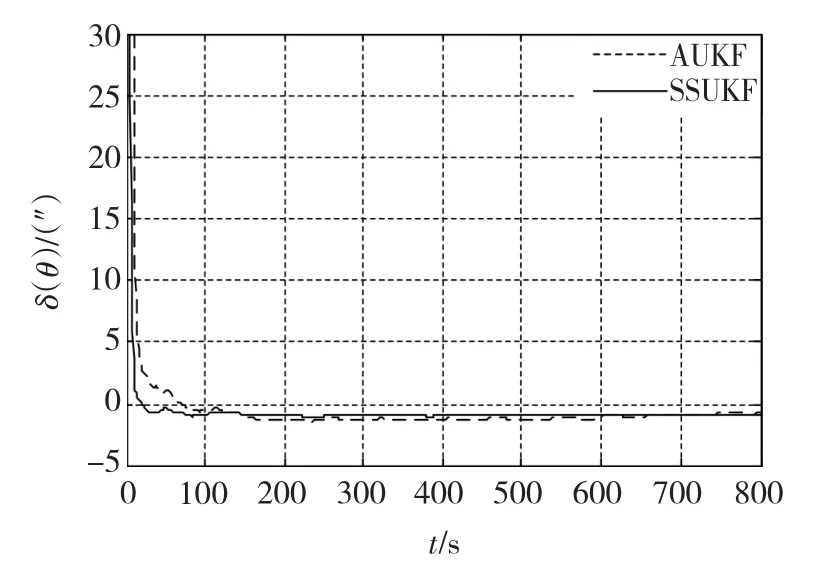
图1 横滚角姿态误差对比Fig．1 Comparison of roll angle errors

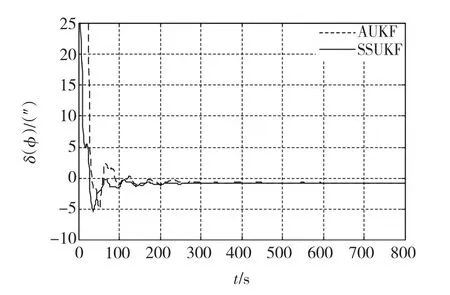
图2 俯仰角姿态误差对比Fig．2 Comparison of pitch angle errors

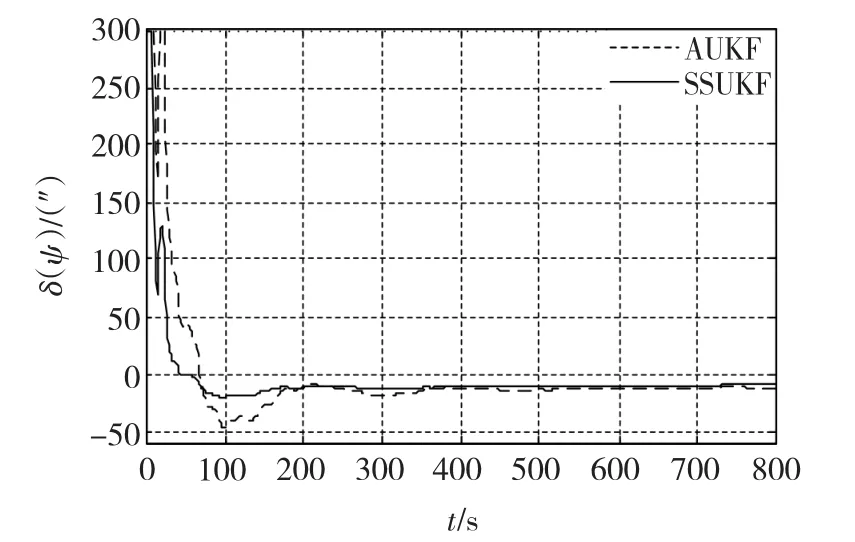
图3 偏航角姿态误差对比Fig．3 Comparison of yaw angle errors

表1 平均一次迭代滤波时间对比Table 1 Time consumption comparison of average one time iteration filter

5 结语

为解决全维姿态UKF算法带来的维数倍增，计算负担加重的问题，本文提出了一种过程和量测不相关的状态切换UKF算法，通过在预测和量测阶段选取不同的状态变量，减小了实时滤波的维数，有效降低了滤波计算量。针对四元数非线性滤波算法中四元数规范化的限制，给出了参数切换UKF算法，通过滤波过程中四元数与修正罗德里格斯参数的实时切换，解决了四元数均值计算和协方差奇异性问题。以实验室SINS/CCD组合姿态估计系统为平台，进行了仿真实验，实验结果验证了所提算法的有效性。

［1］MARKLEY F L．Attitude error representations for Kalman filtering［J］．Journal of Guidance，Control，and Dynamics，2003，63(2):311－317．

［2］CHUNG D Y，LEE J G．Strap-down INS error model for multi-position alignment［J］．IEEE Transactions on Aerospace and Electronic Systems，1996，32(4):1362 －1366．

［3］SHUSTER M D．Constraint in attitude estimation part I:constrained estimation［J］．Journal of the Astronautical Sciences，2003，51(1):51－74．

［4］MARKLEY F Landis，CRASSIDIS J L，CHENG Yang．Nonlinear attitude filtering methods［C］//Collection of Technical Papers-AIAA Guidance，Navigation，and Control Conference，August 15－18，2005，San Francisco，USA．2005，1:753－784．

［5］PSIAKI M L．The super-iterated extended Kalman filter［C］//Collection of Technical Papers-AIAA Guidance，Navigation，and Control Conference，August 16 － 19，2004，Providence，USA．2004，5:3384－3398．

［6］WU Yuanxin，HU Dewen，WU Meiping，et al．Unscented Kalman filtering for additive noise case:augmented vs．non-augmented［C］//Proceedings of the American Control Conference，June 8－10，2005，Portland，USA．2005，6:4051－4055．

［7］JULIER S J，UHLMANN J K．Unscented filtering and nonlinear estimation［J］．Proceedings of the IEEE，2004，92(3):401－422．

［8］MERWE R．Sigma-point Kalman Filters for Probabilistic Inference in Dynamic State-space Models［D］．OGI School of Science and Engineering at Oregon Health and Science University，2004．

［9］MARKLEY F L．Attitude determination using vector observations and the singular value decomposition［J］．Journal of the Astronautically Sciences，1988，36(3):245 －258．

［10］CHOUKROUN D，BAR-ITZHACK I Y，OSHMAN Y．Novel quaternion Kalman filter［J］//IEEE Transactions on Aerospace and Electronic Systems，2006，42(1):174 －190．

［11］CRASSIDIS J L，MARKLEY F L．Unscented filtering for spacecraft attitude estimation［J］．Journal of Guidance，Control and Dynamics，2003，26(4):536 －542．

［12］姜雪原．卫星姿态确定及敏感器误差修正的滤波算法研究［D］．哈尔滨:哈尔滨工业大学控制科学与工程系，2006．

［13］MARKLEY F L，CHENG Yang，CRASSIDIS J L，et al．Averaging quaternions ［J］．Journal of Guidance，Control，and Dynamics，2007，30(4):1193 －1197．