智能断路器抗EFT/B干扰滤波器设计

佟为明， 张忠， 李中伟， 王胤燊

(哈尔滨工业大学电气工程及自动化学院，黑龙江哈尔滨 150001)

0 引言

断路器作为电力系统的重要电器元件之一，被广泛地应用于配电系统中。智能断路器是微处理器技术、网络技术和信息通信技术与现代机电一体化技术高度集成化的综合体。智能断路器由于工作在复杂的电磁环境中，需具备很强的抗干扰能力。因此智能断路器的抗电磁干扰性能变得尤为重要。智能断路器必须通过IEC61000－4－4标准设定的电快速瞬变脉冲群(electrical fast transient/burst)抗扰度试验［1］。由于EFT/B脉冲重复频率高、脉冲上升时间短、单个脉冲能量低、脉冲成群出现，干扰能力强，如果没有良好的应对措施，很难通过试验。电快速瞬变脉冲群对智能断路器干扰是通过电流互感器转换成可操作的模拟信号，叠加的干扰信号会使微处理器产生错误判断，造成误动作，给生产带来重大不可靠因素［2］。为了解决智能断路器由电快速瞬变脉冲群干扰导致的误动作问题，需采取合理控制方案，因此有必要对电快速瞬变脉冲群干扰进行建模和仿真分析。

虽然相关的IEC61000－4－4标准给出了电快速瞬变脉冲群发生器的原理图，指定了其输出部分的隔直电容值和匹配电阻值［1］，但是原理图仅用于说明发生器的工作原理，不能直接进行电快速瞬变脉冲群仿真研究。目前，很多电磁兼容建模研究者主要采用计算或测量方法确定系统参数进行建模分析。文献［3］通过实验测量得到有效的瞬态电磁干扰波形进行电快速瞬变脉冲群发生器的建模。这种方法受到很多测量条件的限制，包括传输电缆型号、耦合夹、接地条件以及负载状况等，而提取的建模参数仍需要修正，同时建立的电快速瞬变脉冲群发生器等效模型也相当复杂。文献［4］提出采用自适应级联扩展卡尔曼滤波器对未知随机偏差建模，将真实值和未知随机偏差一起估计;文献［5］提出线性化近似的扩展卡尔曼滤波算法，近似的线性系统与原非线性系统仍存在一定的误差;文献［6］通过改进的卡尔曼滤波器算法改善非线性模型性能指标。

本文拟采用改进扩展卡尔曼滤波算法，设计抗电快速瞬变脉冲群滤波器，切断电快速瞬变脉冲群干扰途径，提高智能断路器抗干扰的综合能力，满足电磁兼容设计标准。

1 EFT/B干扰源仿真模型建立

在配电系统电路中，断路器切换感性负载时，电路电流发生突变，感性负载两端会产生瞬时高压。在电弧复燃和熄灭的过程中，脉冲电压不断地被复制，引发脉冲群电压。IEC61000－4－4标准规定了电快速瞬变脉冲群抗扰度试验，给出了电快速瞬变脉冲群发生器的原理图，如图1所示。

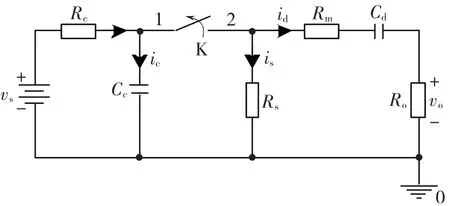
图1 IEC标准给出的EFT/B发生器简化电路Fig．1 Simplified EFT/B Generator Circuit Given by IEC Standard

图1中，Cd为隔直电容;Rm为匹配电阻;vs为直流电源;Cc为储能电容;Rs为内部放电电阻;Ro为外部负载电阻。由于没有给出其他相关参数数据，所以无法直接进行电快速瞬变脉冲群仿真实验［7］。

电快速瞬变脉冲群干扰源电压vo(t)可用双指数函数进行数学描述［8－10］，即

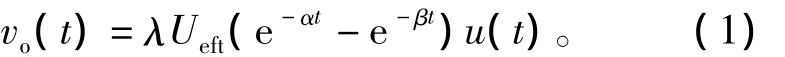
其中:u(t)为单位阶跃函数;α为脉冲下降时间相关函数;β为脉冲上升时间相关函数;Ueft为电快速瞬变脉冲群干扰电压幅值;λ=1.27为波形系数。

在电快速瞬变脉冲群发生电路稳定条件下，当开关K闭合时，电路如图2所示。

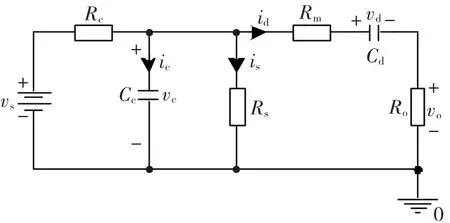
图2 开关K闭合时EFT/B发生器电路Fig．2 EFT/B Generator Circuit with K switched on

图2中，ic为Cc电容电流;id为Cd电容电流;vc为Cc电容电压;vd为Cd电容电压;is为Rs上的电流，vs为输入激励源，有

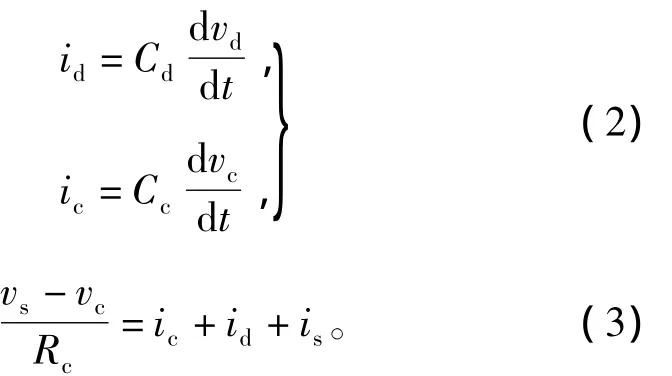
联立式(2)、式(3)得

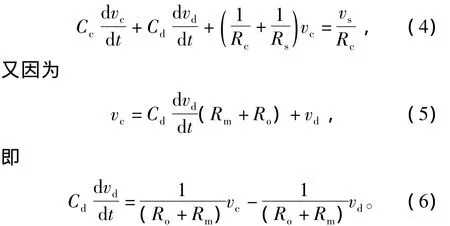
联立式(6)、式(8)得

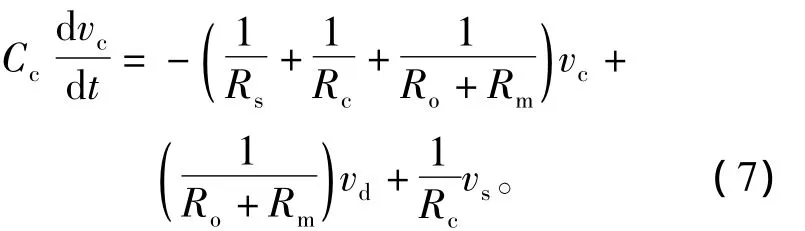
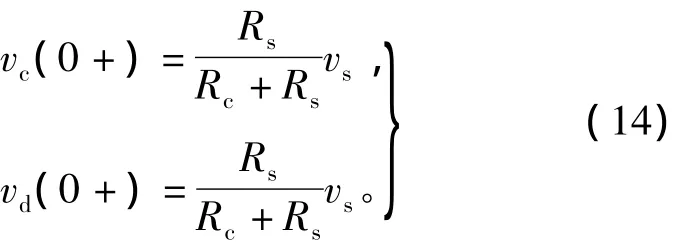
根据换路定律确定初始条件，即

当开关K断开时，电路如图3所示。

图3 开关K断开时EFT/B发生器电路Fig．3 EFT/B Generator Circuit with K switched off

由图3电路建立回路方程为

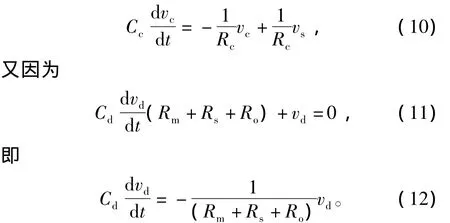
由式(10)、式(12)得

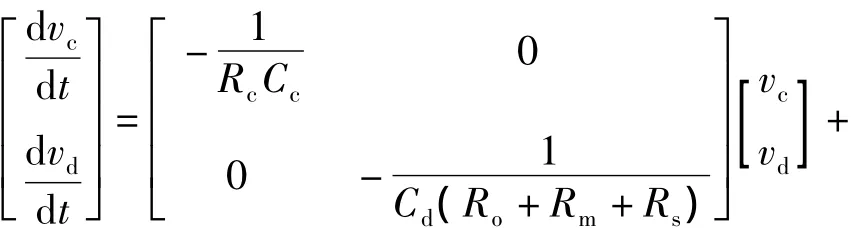
根据换路定律确定初始条件，即

2 EFT/B耦合途径

智能断路器数据采集系统是将检测信号转化为数字量送入微处理器，微处理器将数据通过计算与整定值比较，做出相应判断。数据采集系统包括电压形成、模拟滤波、采样保持、多路开关切换和A/D转换等模块。

由于电快速瞬变脉冲群干扰是通过线间分布电容作用于敏感设备，属于容性干扰，干扰通过线间分布电容耦合，其原理如图4所示。

图4 容性耦合干扰Fig．4 Capacitive coupling interference

图4中，回路1为干扰源线路;回路2为敏感线路;C为线间分布电容;v1为干扰源电压;Rg为回路2对地电阻;R1为回路1电阻;R2为回路2电阻。R2上形成的干扰电压Uf为

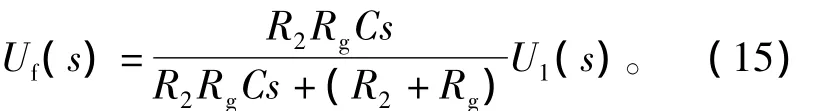
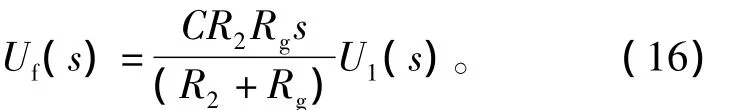
显然干扰电压取决于干扰源工作频率、敏感电路对地电阻以及干扰源电压综合作用。一般而言，干扰源工作频率、敏感电路对地电阻都是确定的，而减小分布电容也不易做到，因此设计抗电快速瞬变脉冲群干扰滤波器就成为提高智能断路器电磁兼容性最佳解决办法。

由于电快速瞬变脉冲群干扰通过线间耦合电容传递到互感器二次侧，从而导致数据采集系统接受错误信号并送入微处理器，做出错误判断，造成智能断路器误动作。因此还需确定线间耦合电容参数。

假设两根平行导线分别通以正、负电流，线电荷密度为ρ，导线半径r，两导线间距为d，x处电场的电场强度Ex，两导线正、负电荷作用于该处的电场分量为Ex1、Ex2，如图5所示。

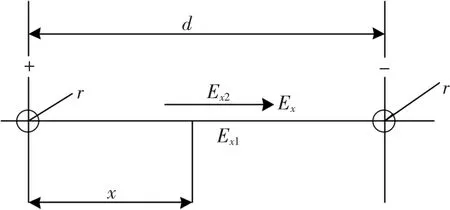
图5 导线间的电场强度示意图Fig．5 Diagram of field strength E between wires

根据高斯定理，有

式中，ε为介电常数。

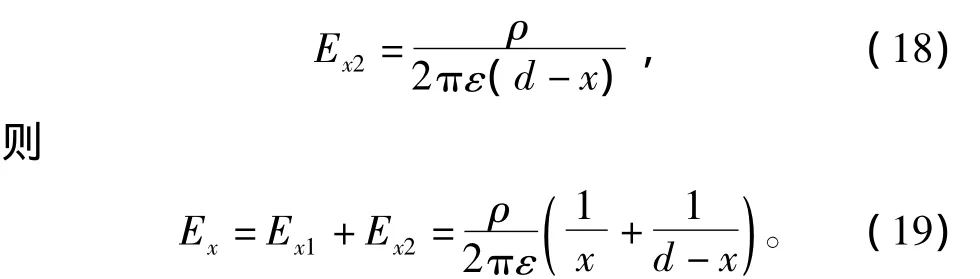
两导线间电压为

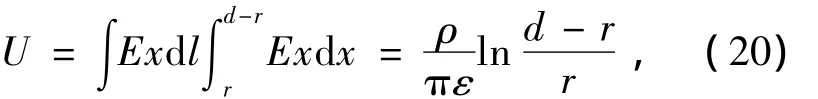
两导线间单位长度的分布电容为

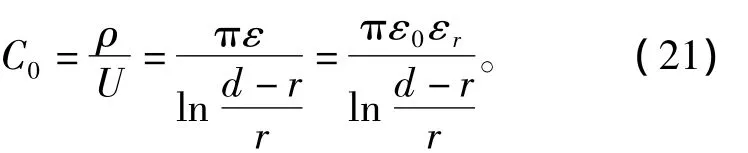
3 抗EFT/B干扰扩展卡尔曼滤波器设计

抗电快速瞬变脉冲群干扰最好的方法是设计专门的滤波器。目前，很多研究学者都采用扩展卡尔曼滤波算法，研究表明扩展卡尔曼滤波器可以有效滤除智能断路器非线性系统干扰。

扩展卡尔曼滤波器实质是通过线性化达到渐进最优贝叶斯决策的状态估计器。假定动态噪声和量测噪声是均值为零的正态白噪声序列，即

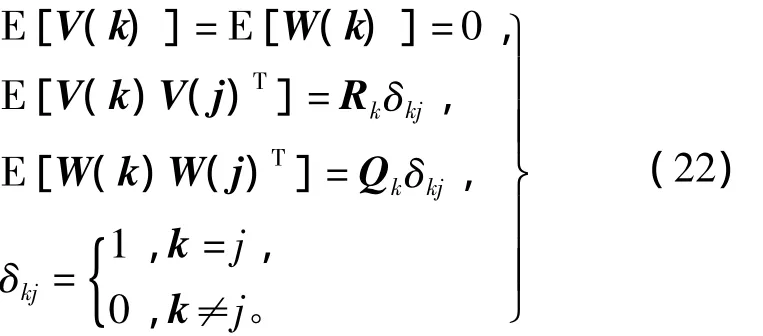
式中:k为离散时间变量;Qk为k时刻的动态噪声方差阵;Rk为k时刻的量测噪声方差阵;Wk为k时刻的过程噪声和Vk为k时刻的观测噪声。

对于离散时间系统非线性动态方程和非线性量测方程可以用非线性差分方程表示为

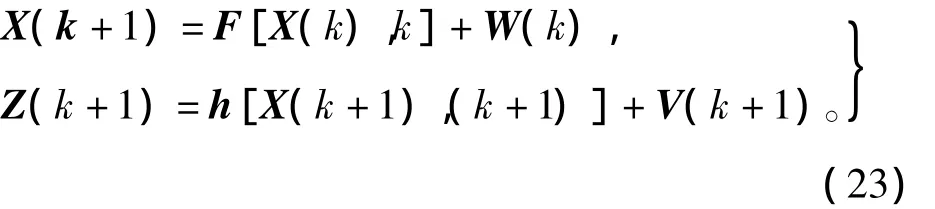
其中:X(k)为n维随机状态向量序列;Z(k)为m维观测状态向量序列;W(k)为r维随机动态噪声;V(k)为m维随机量测噪声;h(k)为n维向量函数。

假设在k时刻已量测，Z1，Z2，…，Zk向量，并且估计状向量(以下带有“^”表示为估计量)。预测第k+1时刻的量测向量Zk+1后，求出该时刻的状态估计向量，并使状态向量的方差误差最小，即

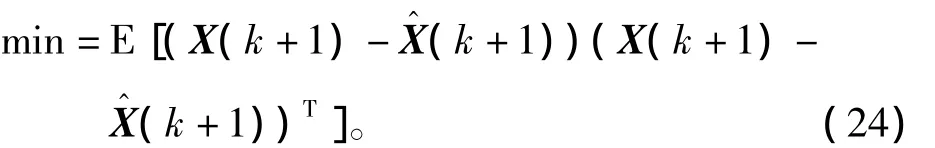
将F［X(k)，k］在(k)处展成泰勒级数，忽略高阶导数项，则

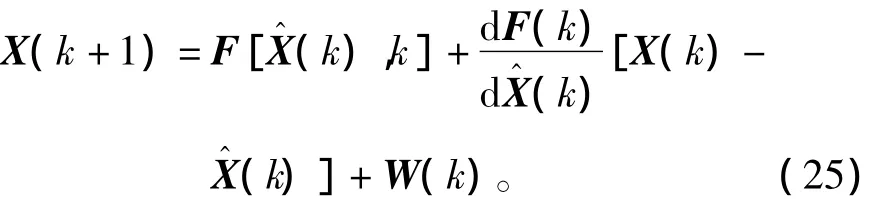
将h［X(k)，k］在(k+1)处展成泰勒级数，忽略高阶导数项，则

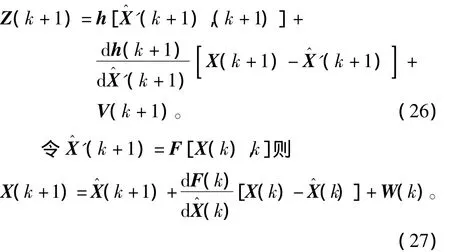
整理式(17)、式(18):

其中，Kk为卡尔曼增益阵。

卡尔曼增益阵为

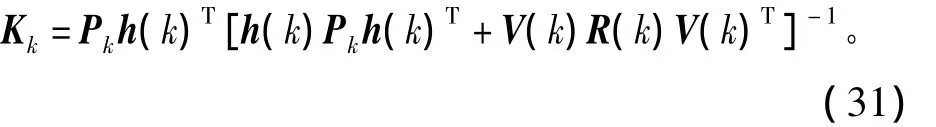
k+1时刻估计状态为

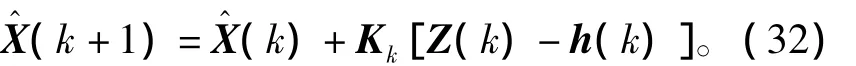
经过数学变换后可得线性化后的扩展卡尔曼滤波方程

1)后验估计方程

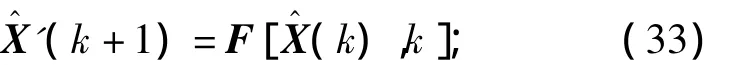
2)预测估计误差方阵

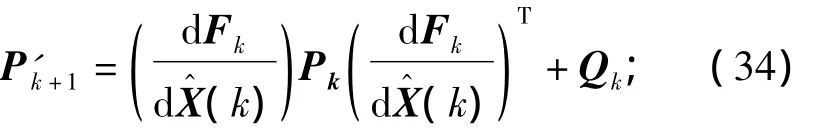
3)卡尔曼增益阵

4)状态估计向量

5)误差方差阵

(3)由于浮选金精矿产率较小，金、铅浮选分离及铅细磨浸出工艺生产成本增加有限，远低于所获铅精矿以及金、银增加回收率所增效益。针对日处理24 t的金浸出系统，半年可收回基建投资。

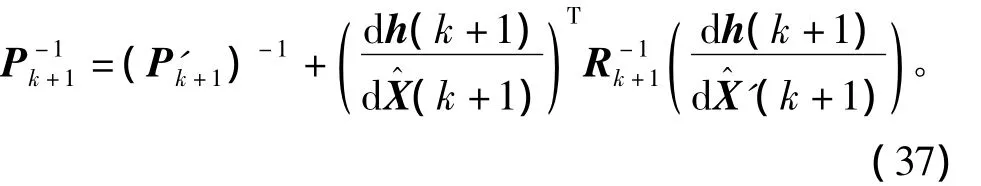
由于观测更新的迭代是利用Gauss－Newton方法求解最小方差，线性化时，由于忽略了高阶导数项，无法保证估计误差一致减少，由此会带来算法不稳定的问题。为了解决这一问题，本文采用Levenberg－Marquardt方法调整预测协方差阵，然后用修正带协方差阵进行迭代更新。如下给出基于Levenberg－Marquardt优化方法的NIEKF滤波算法

卡尔曼增益阵为

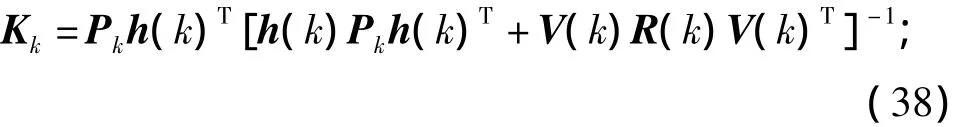
状态估计向量为

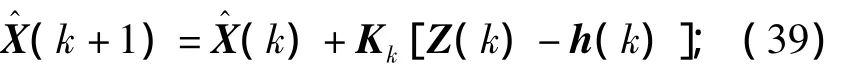
更新协方差阵为

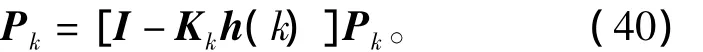
Levenberg－Marquardt优化法设计抗电快速瞬变脉冲群干扰扩展卡尔曼滤波器原理图如图6所示。

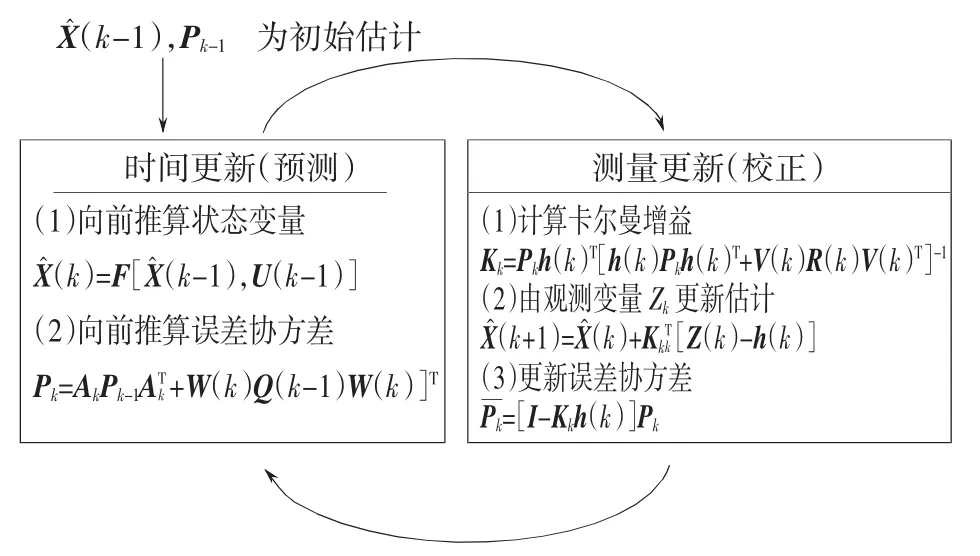
图6 扩展卡尔曼滤波器原理Fig．6 Extended Kalman filter schematic

改进的扩展卡尔曼滤波器算法步骤如下:

1)建立电快速瞬变脉冲群干扰发生初始时刻的状态特性;

2)建立采样时刻的电快速瞬变脉冲群噪声方差阵Qk和量测噪声方差阵Rk;

3)计算预测估计误差方差阵

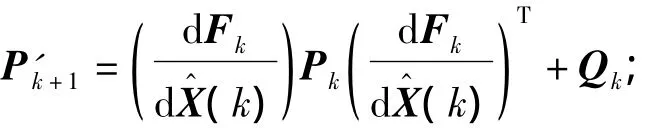
4)计算卡尔曼增益阵

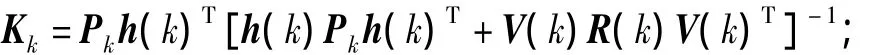
5)计算状态估计向量

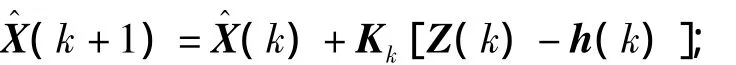
6)计算误差方差阵

7)重返3)进行迭代计算，直到k=N为止。

4 仿真验证

采用Matlab仿真软件设计了电快速瞬变脉冲群干扰电流互感器电路仿真系统，其主电路、电快速瞬变脉冲群发生电路及检测电路如图7所示。图8为幅值4 000 V的电快速瞬变脉冲群干扰源频谱，电快速瞬变脉冲群干扰频宽达到2 MHz。图9为电快速瞬变脉冲群干扰电流互感器二次侧输出电压波形频谱图，仿真实验表明。互感器二次侧电流已经被严重干扰，干扰远高于有用信号幅值，当干扰进入微处理器，将导致智能断路器误判。

由图10和图11非线性系统滤波结果可知，改进的卡尔曼滤波器估计精度和均方差曲线趋势与理论分析一致，即NIEKF滤波方法比EKF精确度更高，同时EKF的均方差在80～90步时，其偏离值过高，如果系统非线性模型不精确时，其结果将不收敛，导致算法失效。相比而言，NIEKF滤波算法具有更高的精度和稳定性。图12为电快速瞬变脉冲群干扰通过改进的卡尔曼滤波器后输出电压波形，仿真实验表明电快速瞬变脉冲群干扰已经被有效滤除。

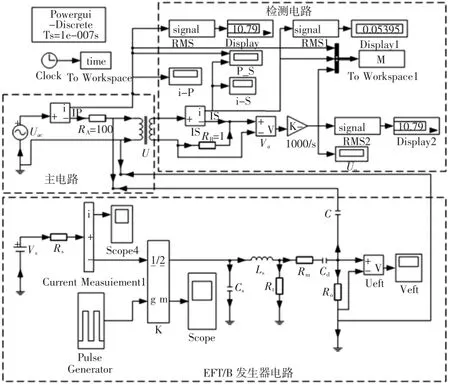
图7 EFT/B干扰电流互感器电路仿真系统Fig．7 Simulation system of EFT/B interference current transformer circuit

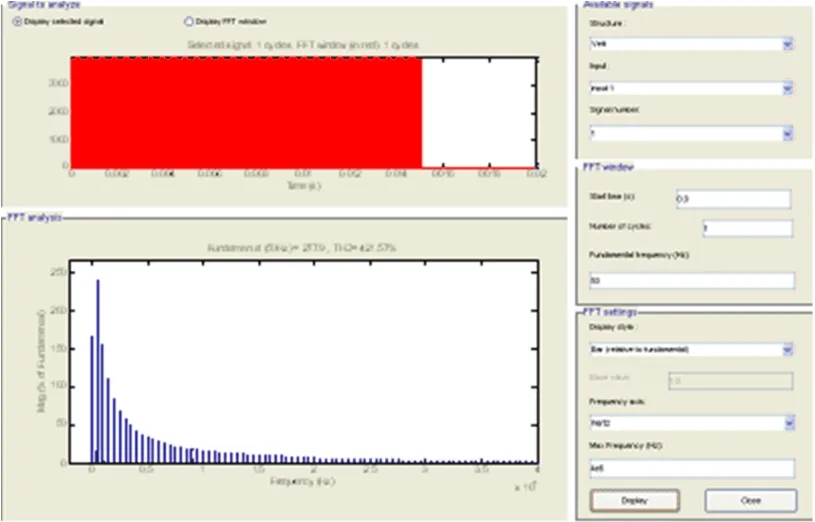
图8 幅值为4 000V EFT/B干扰源频谱Fig．8 Spectrum of EFT/B interference source at the amplitude as 4 000 V

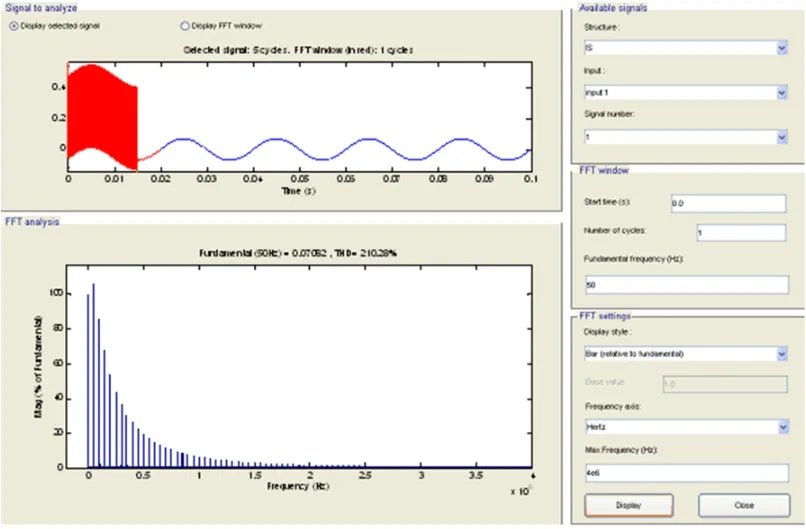
图9 施加EFT/B干扰后电流互感器输出电压频谱Fig．9 Spectrum of current transformer output voltage with EFT/B interference

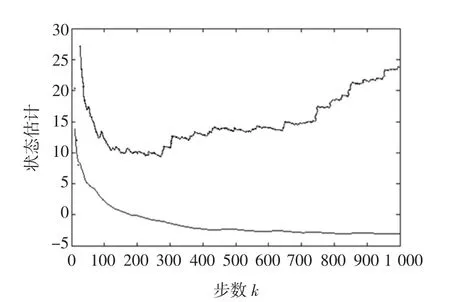
图10 NIEKF与EKF X(k)估计误差曲线Fig．10 Estimated error curve for NIEKF and EKF X(k)

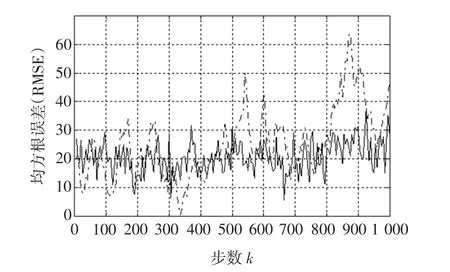
图11 NIEKF与EKF X(k)均方根误差曲线Fig．11 RMS error curve of NIEKF and EKF X(k)

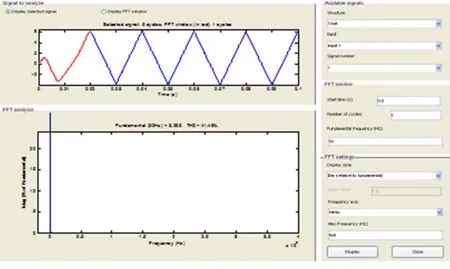
图12 加入NIEKF滤波器后电流互感器输出电压频谱Fig．12 Spectrum of current transformer output voltage with NIEKF filter

5 结语

本文基于电快速瞬变脉冲群干扰作用机理，建立了电快速瞬变脉冲群发生器的等效电路模型，给出了电快速瞬变脉冲群发生器系统状态方程，提出了一种新的抗电快速瞬变脉冲群干扰扩展卡尔曼滤波器算法。新方法采用Levenberg－Marquardt方法优化调整预测协方差阵进行迭代更新，加快了控制对象的收敛速度，弥补了扩展卡尔曼滤波算法精度低且稳定性差的缺点。因此，本方法所进行的改进创新具有较大的理论价值。

［1］IEC61000－4－4．Electromagnetic－Compatibility Testing and Measurement Techniques，Electrical Fast Transient/burst Immunity Test［S］，1995．

［2］王剑乔，刘建新．微机保护抗电快速瞬变脉冲群干扰的研究［J］．高电压技术，2005，31(10):36－38．

WANG Jianqiao，LIU Jianxin．Research on electrical fast transient immunity for relay protection equipment［J］．High Voltage Engineering，2005，31(10):36 －38．

［3］WIGGINS C M，NICKEL F S，HANEY A J．Mobile transient measurement system［J］．IEEE Symposium on EMC，Session2C，1987:42－54．

［4］KWANG Hoon Kim，JANG Gyu Lee，CHAN Gook Park．Adaptive two stage extended kalman filter for a fault-tolerant INS-GPS loosely coupled System［J］．IEEE Trans Aerospace and Electronic Systems，2009，45(1):25 －137．

［5］ROUTRAY A，PRADHAN A K，RAO K P．A novel Kalman filter for frequency estimation of distorted signals in power systems［J］．IEEE Transactions on Instrumentation and Measurement，2002，51(3):469－479．

［6］李良群，姬红兵，罗军辉．迭代扩展卡尔曼粒子滤波器［J］．西安电子科技大学学报，2007，34(2):233－238．

LI Liangqun，JI Hongbing，LUO Junhui．Iterated extended kalman particle filtering［J］．Journal of Xidian University，2007，34(2):233－238．

［7］MUSOLINO F，FIORI F．Modeling the IEC61000 －4 －4 EFT injection clamp［J］．IEEE Trans on Electromagnetic Compatibility，2001，43(1):37 －44．

［8］陈曦，陆俭国，许浩．继电器引起的电快速瞬变脉冲群干扰及抗扰度措施［J］．继电器，2001，29(10):70 －73．

CHEN Xi，LU Jianguo，XU Hao．Disturbance rejection degree and countermeasures to the disturbance of electric fast transient pulse caused by relays［J］．Relay，2001，29(10):70 － 73．

［9］全国无线电干扰标准化委员会．电磁兼容标准汇编［S］．北京:中国标准出版社，2002．

［10］CERRI G，DE Leo R，PRIMIANI U M．Electrical fast-transient test:conducted and radiated disturbance determination by a complete source modeling［J］．IEEE Trans on Electromagnetic Compatibility，2001，43(1):37 －44．