基于鲁棒迭代学习的永磁直线电机控制

张宏伟， 余发山， 卜旭辉， 王福忠

(河南理工大学电气工程与自动化学院，河南焦作454000)

0 引言

永磁同步直线电机(permanent magnet linear motor，PMLM)是一种将电能直接转化成直线运动机械能的传动装置［1］，近年来被广泛应用于工业领域。由于直线电机的齿槽效应、端部效应、系统参数(动子质量、粘滞摩擦系数等)的变化、摩擦阻力的非线性变化等因素的存在，直线电机系统是一个多变量、时变的非线性系统，传统的PID控制方法针对这类非线性系统很难实现精确控制［2］。虽然自适应控制［3－4］，鲁棒控制［5－6］，神经网络控制［7］，滑模控制［8］等方法可以获得比PID控制方法更好的输出性能，但是无法实现有限区间内的完全跟踪，而且很难处理直线电机内部的各种扰动，如负载变化、齿槽效应力、摩擦力、纹波推力等。

针对执行重复任务的直线电机，迭代学习控制(iterative learning control，ILC)可以实现有限区间内完全跟踪，而且还可以处理系统中由齿槽效应力、摩擦力、纹波推力、端部效应力等因素引起的重复或周期性扰动［9－13］。然而，在直线电机速度和位置跟踪控制过程中，需要对速度信号或位置信号进行测量，由于传感器自身特性和外部环境的影响，测量信号中不可避免地存在测量扰动。测量扰动为迭代不重复的扰动，其取值是随机的，理论已经证明常规的ILC算法对于这类扰动无能为力［14－15］。文献［10］的研究结果也指出，由于存在这种迭代变化的测量扰动，采用P型ILC算法控制的直线电机速度输出和位置输出存在较大的波动［10］。

本文提出一种带有衰减因子的鲁棒ILC算法，在原有P型ILC算法的基础上引入一个衰减因子，并将提出的算法应用于直线电机的速度和位置跟踪控制。

1 永磁直线电机的控制模型

由式(1)～式(4)可知，永磁直线电机是一个典型的非线性、多变量、时变的系统，其跟踪控制一直是控制领域的难点问题。对于执行重复任务的直线电机，ILC可实现速度和位置在有限区间内的完全跟踪，还可以处理诸如齿槽效应力、摩擦力、纹波推力、端部效应力等因素引起的重复或周期性扰动［9－13］。但对迭代不重复的测量扰动，迭代学习控制无能为力。为此，本文提出一种带有衰减因子的鲁棒ILC算法，其主要做法就是在P型ILC算法的误差项之前引入一个衰减因子，该因子随着学习次数的增加逐步趋近于零。由于测量扰动是通过误差引入的，因此当学习次数增加时该项的值逐渐减小，从而抑制测量扰动。

2 鲁棒ILC算法设计

2.1 算法设计

针对如式(1)～式(4)所示的永磁直线电机控制模型，考虑如下一类具有一般性的非线性重复系统，即

上述3个假设对于执行重复任务的直线电机都是满足的。假设1中的Lipschitz条件无论对于非线性的摩擦力方程式(3)还是非线性的脉动力方程式(4)都是成立的。假设2为直线电机执行重复任务的条件。假设3为对于给定任务，直线电机能控的条件。

在非线性系统式(5)控制的过程中，需要对输出信号yk(t)进行测量。当系统存在测量扰动wk(t)时，系统的测量输出为

文献［14－15］的研究结果表明，对于存在测量扰动的非线性系统，采用P型ILC算法得到的收敛性结果仅为有界收敛，即跟踪误差εk(t)收敛到一个与扰动上界有关的域内。

本文提出带有衰减因子的鲁棒ILC算法，即

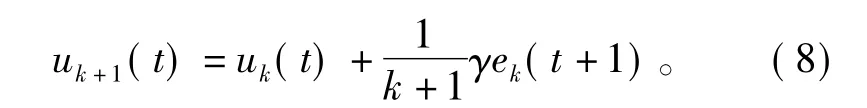
式中:k为迭代次数;γ为学习增益因子。

2.2 收敛性分析

定理中的结论是针对SISO的非线性系统式(5)给出的，当系统式(5)为MIMO的非线性系统时，可以得到同样的结论。

3 仿真研究

3.1 永磁直线电机仿真参数

本文采用Matlab软件对提出的鲁棒ILC算法进行仿真验证。永磁直线电机的仿真参数设置为:10 N·s·m－1;b1=8.5 N;ω0=100 rad/s。仿真过程中采样周期取0.001 s。

直线电机的期望位置和期望速度设计为

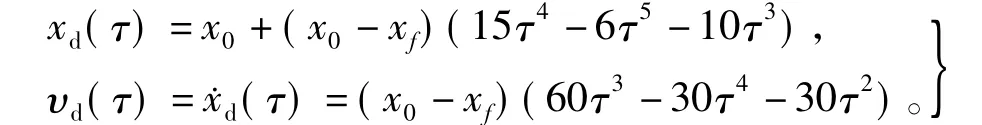
式中:τ=t/(tf－t0)，t0为初始时间，tf为终止时间;x0为初始位置;xf为终止位置。仿真中x0=0，xf=0.2 m，tf=1 s。假设位置测量过程中存在幅值为0.01的白噪声扰动信号。分别采用P型ILC算法以及带有衰减因子的鲁棒ILC算法进行控制，并比较仿真结果。

3.2 P型ILC控制

采用P型ILC控制算法，即uk+1(t)=uk(t)+0.8ek(t+1)对直线电机进行跟踪控制的仿真结果如图1、图2所示。

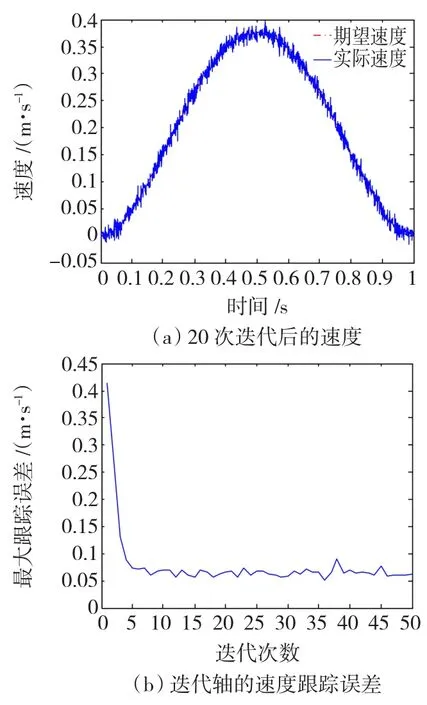
图1 采用ILC控制的速度跟踪结果Fig．1 The speed tracking with ILC

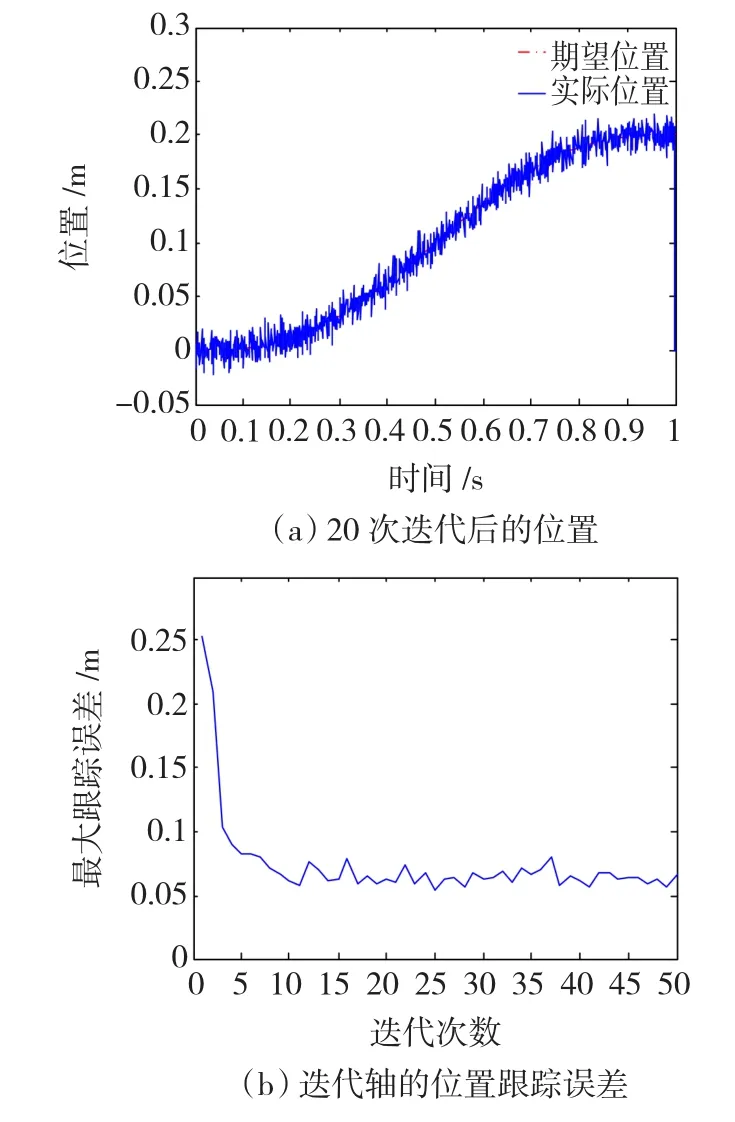
图2 采用ILC控制的位置跟踪结果Fig．2 The position tracking with ILC

图中给出了20次迭代以后的速度跟踪和位置跟踪效果，并给出了沿迭代轴方向的最大跟踪误差。由仿真结果可知，ILC控制经过20次的迭代过程以后可以达到整个区间的跟踪，不需要过渡过程，但是由于测量扰动的影响，使得直线电机的速度输出和位置输出存在一定的波动，跟踪性能相对较差。

3.3 鲁棒ILC控制

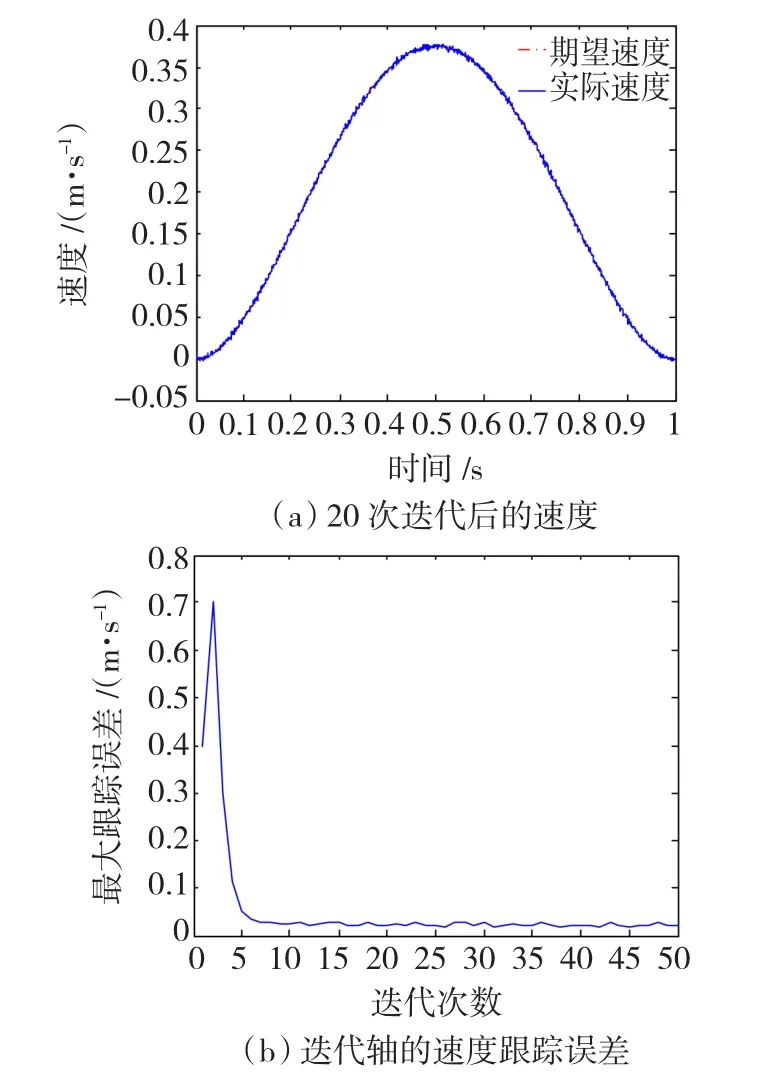
图3 采用鲁棒ILC控制的速度跟踪结果Fig．3 The speed tracking with robust ILC

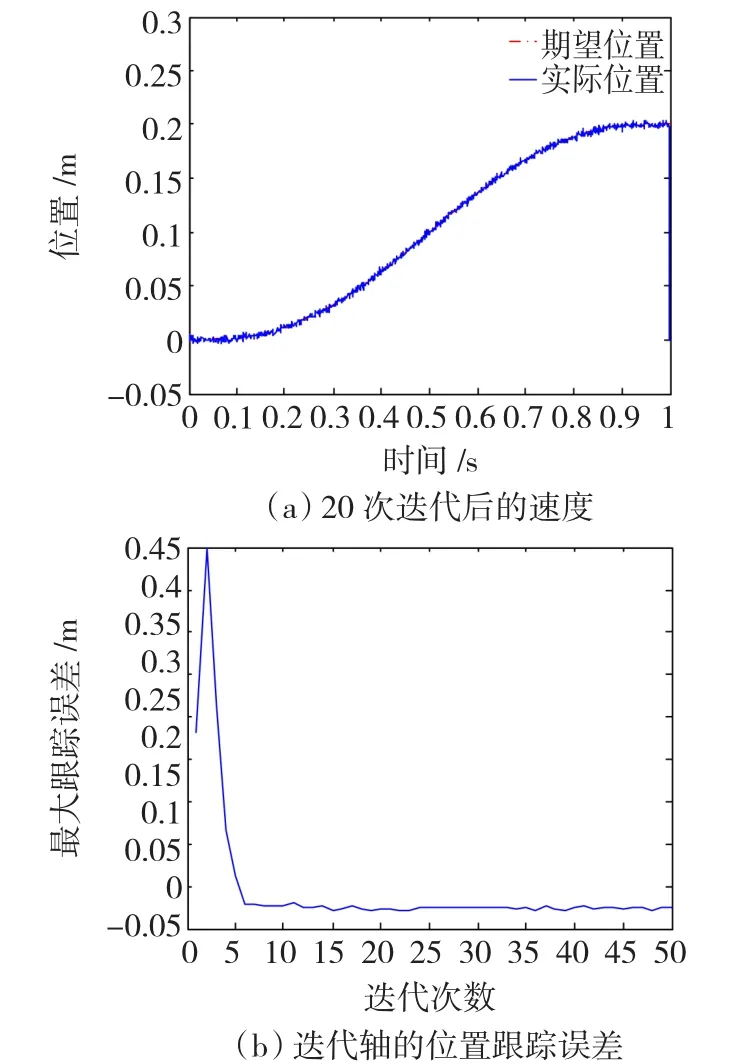
图4 采用鲁棒ILC控制的位置跟踪结果Fig．4 The position tracking with robust ILC

图中给出了20次迭代以后的速度跟踪和位置跟踪效果，并给出了沿迭代轴方向的最大跟踪误差。与P型ILC的控制结果相比，鲁棒ILC控制算法可以有效抑制测量扰动，具有得较好的速度和位置跟踪性能，其迭代轴上的速度和位置跟踪误差也远远小于P型ILC控制算法，如图3(b)、图4(b)所示。

4 结论

本文针对测量扰动对永磁直线电机迭代学习速度和位置跟踪控制的影响，提出一种带有衰减因子的鲁棒ILC算法。理论上分析了该算法的收敛性，并通过仿真实验验证了所提算法的有效性。研究结果表明:

1)当测量扰动有界时，本文提出的鲁棒ILC算法理论上可保证跟踪误差收敛到零，而P型ILC算法仅能保证跟踪误差收敛到一个与扰动信号上界有关的域内，因此该算法对测量扰动具有较强的鲁棒性。

2)鲁棒ILC算法不仅可以实现有限区间内直线电机速度和位置的完全跟踪，而且还可以有效抑制测量扰动，其跟踪性能明显优于P型ILC控制算法。

3)本文提出的鲁棒ILC控制算法不限于对永磁直线电机的速度和位置跟踪控制，也可以应用于其他重复非线性系统的测量扰动抑制。

［1］ 叶云岳．直线电机原理与应用［M］．北京:机械工业出版社，2000:1－10．

［2］ OTTEN Gerco，DE VRIES Theo J A，VAN AMERONGEN Job，et al．Linear motor motion control using a learning feedforward controller［J］．IEEE/ASME Transactions on Mechatronics，1997，2(3):179－187．

［3］ TAN K K，LEE T H，HUANG S N，et al．Adaptive predictive control of a class of SISO nonlinear systems［J］．Dynamics and Control，2001，11(2):151 －174．

［4］ 曹荣敏，侯忠生．直线电机的非参数模型直接自适应预测控制［J］．控制理论与应用，2008，25(3):587－590．CAO Rongmin，HOU Zhongsheng．Nonparametric model direct adaptive predictive control for linear motor［J］．Control theory ＆application，2008，25(3):587－590．

［5］ 李义强，周惠兴，王先逵，等．直线电机伺服定位系统时间最优鲁棒控制［J］．电机与控制学报，2011，15(3):13－18．LI Yiqiang，ZHOU Huixing，WANG Xiankui，et al．Robust timeoptimal control of a linear motor positioning system［J］．Electric Machines and Control，2011，15(3):13 －18．

［6］ 赵希梅，郭庆鼎．永磁直线同步电动机的变增益零相位H∞鲁棒跟踪控制［J］．中国电机工程学报，2005，25(20):132－136．ZHAO Ximei，GUO Qingding．Variable gain zero phase H∞robust tracking control for permanent magnet linear synchronous motor［J］．Proceedings of the CSEE，2005，25(20):132－136．

［7］ 王丽梅，武志涛，左涛．永磁直线电机自构式模糊神经网络控制器设计［J］．电机与控制学报，2009，13(5):643－647．WANG Limei，WU Zhitao，ZUO Tao．PMLSM self-constructing fuzzy neural network controller design［J］．Electric Machines and Control，2009，13(5):643－647．

［8］ 王艳敏，冯勇，陆启良．永磁同步电动机的无抖振滑模控制系统设计［J］．电机与控制学报，2008，12(5):514－520．WANG Yanmin，FENG Yong，LU Qiliang．Design of free-chattering sliding mode control systems for permanent magnet synchronous motor［J］．Electric Machines and Control，2008，12(5):514－520．

［9］ TAN K K，LEE T H，LIM S Y，et al．Learning enhanced motion control of permanent linear motor［C］//Proceedings of IFAC International Workshop on Motion Contro1，September 21－23，1998，Grenoble，France．1998:357 －364．

［10］ TAN K K，DOU H F．High precision linear motor control via relay-tuning and iterative learning based on zero-phase filtering［J］．IEEE transactions on control system technology，2001，9(2):244－253．

［11］ LEE T H，TAN K K，LIM S Y，et al．Iterative learning control of permanent magnet linear motor with relay automatic tuning［J］．Mechatronics，2000，10(1－2):169－190．

［12］ 杨俊友，马航，关丽荣，等．永磁直线电机二维分段复合ILC控制［J］．中国电机工程学报，2010．30(30):74－80．YANG Junyou，MA Hang，GUAN Lirong，et al．Two-dimensional segmented synthesis iterative learning control of permanent magnet linear motor［J］．Proceedings of the CSEE，2010，30(30):74－80．

［13］ 石阳春，周云飞，李鸿，等．长行程直线电机的ILC［J］．中国电机工程学报，2007，27(24):92－96．SHI Yangchun，ZHOU Yunfei，LI Hong，et al．Research on iterativelearning control to long stroke linear motor［J］．Proceedings of the CSEE，2007，27(24):92－96．

［14］ WANG Danwei．Convergence and robustness of discrete time nonlinear systems with iterative learning control［J］．Automatica，1998，34(11)，1445－1448．

［15］ SAAB S S．Selection of the learning gain matrix of an iterative learning control algorithm in presence of measurement noise［J］．IEEE Transactions on Automatic Control，2005，50(11):1761－1774．

［16］ XU Jianxin，XU Jing，LEE T H．Iterative learning control for systems with input deadzone［J］．IEEE Transactions on Automatic Control，2005，50(9):1455 －1459．