可列个无穷小积的极限的存在性分析

杨 挺

可列个无穷小积的极限的存在性分析

杨 挺

摘 要：文章辨析了“可列个无穷小的积一定是无穷小”这一结论中的疑义，应用二重极限的概念分析了产生这一问题的原因，在构造了两个反例的基础上，给出了这一命题成立的两个充分条件。

关键词：教学研究；高等数学；无穷小；可列积；充分条件

杨挺/连云港体育运动学校讲师（江苏连云港222000）。

无穷小是极限理论中的重要概念，通常在教材中把无穷小与无穷大两个内容合并列为一个小节，并把无穷小的阶的比较进行研究和讨论，由此可见其重要性。在讲述无穷小概念的时候，直接给出下面的定理。

定理1 无穷小与有限函数的乘积是无穷小。

定理2 有限个无穷小的和是无穷小。

定理3 有限个无穷小的积是无穷小。

前两个定理都容易理解，对于定理3，无穷多个无穷小的乘积是什么呢？难道可能不是无穷小吗？几乎每年都有学生会提出这样的问题，而且难以解释清楚。实际上，在教师中也常常会存在着这样的疑问。

一、错误起因

理解的错误产生于数学归纳法的应用。

例1 用数学归纳法证明：无穷多个无穷小的乘积是无穷小。

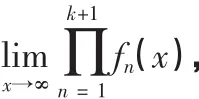
正是由于例1的证明，很多人错误地认为：可列个无穷小的乘积必是无穷小。不幸的是，此证明过程是错误的，其根源在于忽略了无穷小结构本身的特殊性和二重极限的复杂性。

二、错误辨析

实际上，对此命题正确性的讨论最好是在学生学习过二重极限之后，此时学生的认知水平、知识储备达到一定程度才能真正理解和掌握。

由定义1和定义2，类似可定义函数f（x,y）在无穷远点处的二重极限，以及先对x再对y的二次极限。

对于二重极限与二次极限的关系，以下三个结论是共知的：

函数的二重极限存在，两个二次极限不一定存在，即使二次极限都存在也不一定相等。

函数的两个二次极限都存在且相等，二重极限不一定存在。

函数的两个二次极限不一定都存在。

1.函数的情形。这里讨论自变量x→∞时的函数无穷小序列的情形，其它自变量变化过程可类似分析。

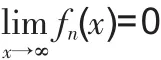
是否为0。

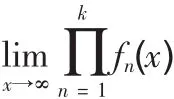
2.数列的情形。

三、两个实例

上述两个例题说明了当函数值（数列值）由两个变量决定时，可列个无穷小的乘积可能不是无穷小，进一步的，当决定数值的变量更多时，其变化形式将更加复杂，可列个无穷小的乘积不是无穷小的实例将更多。

四、可列个无穷小的乘积是无穷小的充分条件

产生上述问题的主要根源在于，在变量变化过程中，函数值可能会受到多个变量的影响，任意一个变量都不可能决定函数的取值及变化趋势。

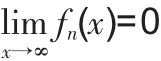
仿此可定义x→x0时及其它自变量变化过程时的一致无穷小函数序列，也可以类似定义一致无穷小数列序列。

证明：对任意的 ε＞0，存在 M＞0（M与 n无关），使得当 |x|＞M时，恒有 |fn(x)|＜ε，因此不妨设 ε＜1，则有

推论2数列{anm|n=1,2，Λ}是无穷小数列序列，且单调递减，则其可列积

证明类似于定理1，略。

由定理1和定理2以及函数极限存在的充要条件，可得如下推论：

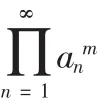
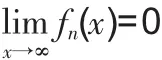
推论2的证明略。

中图分类号：O171

A

1671-6531（2012）11-0033-02

：姚 旺