SMA 纤维复合材料变截面板簧固有频率特性研究

徐晓明，任勇生，杜向红

(山东科技大学 机械电子工程学院，青岛 266510)

悬架是现代汽车的重要总成之一，起着连接车轮与车架并传递其一切力与力矩，缓和不平路面对车身的冲击载荷，衰减车身振动的作用，保证汽车平顺的行驶。半主动悬架减振器的阻尼和弹性元件的刚度可以根据路面情况进行调节，通过实时调节悬架系统的阻尼和刚度，可以改变减振器的阻尼系数和系统的固有频率，降低和避免车辆的共振。半主动悬架相比被动悬架，增加了自动调节装置，通过合适的控制策略调节悬架的阻尼和刚度以更好的适应路面的变化;相比主动悬架，又是一种无源控制，作动器能耗低，结构简单，价格低廉，而且控制品质接近主动悬架。因此，发展半主动悬架，特别是基于智能材料的半主动悬架系统的研究与开发，具有重要的理论价值与实际意义［1］。

目前智能材料在汽车半主动悬架可调减振系统中的应用研究，绝大多数采用电、磁流变液为工作介质，来调节减振器的阻尼系数，而以调节弹性元件可控环节的刚度和固有频率的研究报道却相当少见。事实上，电、磁流变半主动悬架还存在性能稳定性、维护等方面的缺陷。

迄今为止，SMA智能材料在复合材料梁、板类结构的固有频率调节方面的应用研究，已经获得了很大的进展。将SMA纤维埋入复合材料，设计变截面板簧半主动悬架，在理论与实践方面，存在一定的可行性。李磊等［2］建立了具有预应变的SMA纤维复合材料等截面板簧的分析模型，导出了板簧刚度的数学表达式，并且通过数值计算得到板簧的刚度随温度的升高、SMA纤维体积分数、铺层方式等参数的变化曲线。徐晓明等［3］建立了具有预应变的SMA纤维复合材料变截面板簧的分析模型，用瑞利－里兹法推导出板簧刚度的表达式，通过计算得到变截面板簧的刚度随温度的升高与降低、SMA纤维体积百分数、基体材料铺层角等参数的变化曲线。上述研究都是关于形状记忆合金复合材料板簧模型的静力学分析，而板簧作为汽车悬架的组成部分，还需要进一步研究其振动特性。王洪礼等［4］对带有SMA智能材料的刚度可调汽车半主动悬架进行随机振动的可靠性分析，其中的SMA以螺旋弹簧的形式出现，着重研究半主动悬架车辆随机振动以及控制策略而不涉及弹簧本身动力性能的研究。固有频率是结构的重要动力特性之一，确定和计算固有频率是结构动力分析的一个重要任务。为避免共振，应当使激励频率与梁的固有频率尽量分开。在结构振动中，相对更容易发生的低阶固有振动，由于其破坏板簧所需的能量越小，是更容易使板簧受到破坏的振型［5］。因此，板簧的固有频率，尤其是低阶固有频率的设计与计算，在理论与实际中显得尤为重要。

本文根据Brinson提出的SMA本构关系理论，结合复合材料的层合理论，建立SMA纤维复合材料变截面板簧的自由振动分析模型，应用瑞利－里兹数值近似计算方法，计算和分析了板簧固有频率在一个完整的升温－降温过程的变化规律，以及基体材料纤维铺层角度、SMA纤维含量和SMA/环氧铺层位置的影响，揭示了SMA纤维复合材料变截面板簧的固有频率调节机理。

1 SMA完全约束回复的Brinson一维本构关系理论

SMA材料具有“智能”特性，它既有传感功能(感知和接收应力、应变、电、热等信号)，又具有驱动功能(对激励产生响应)［6］。使具有初始残余变形并完全约束的SMA升温，会产生很大的形状回复力。这个SMA完全约束回复应力可以由Brinson模型描述如下［7］，模型中涉及符号的意义如表1所示。

表1 本构方程中的术语Tab.1 The terminology of constitutive equation

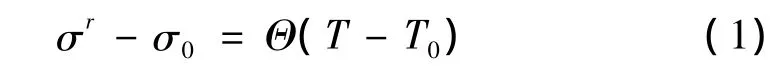
当 Aσs≤T ≤Aσf时，温度诱发马氏体向奥氏体的相变:

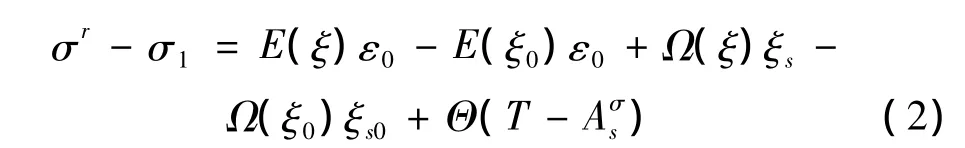
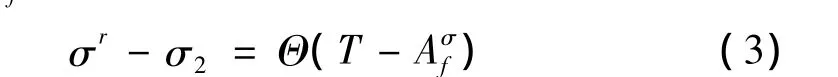
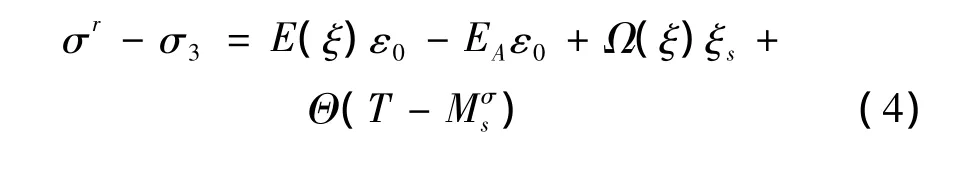
升温和降温的相变动力学方程分别为:

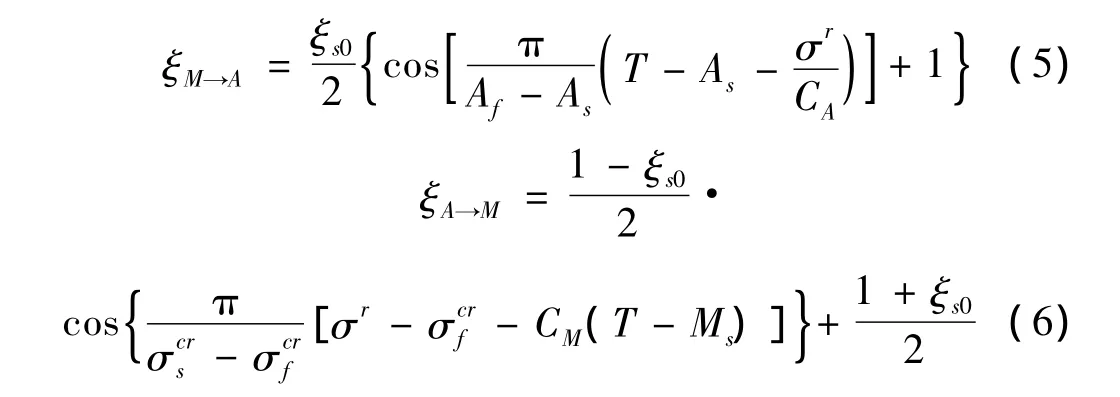
弹性模量与相变张量分别为:

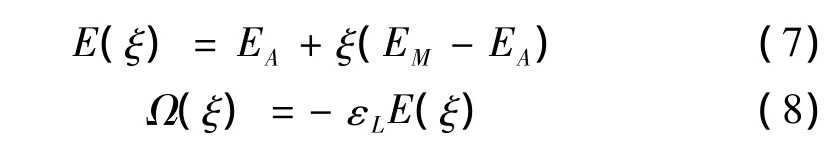
2 嵌入SMA纤维的复合材料变截面板簧

2.1 具有SMA纤维的各向异性层合梁的本构方程

SMA纤维混杂各向异性层合梁的本构方程为［8］:

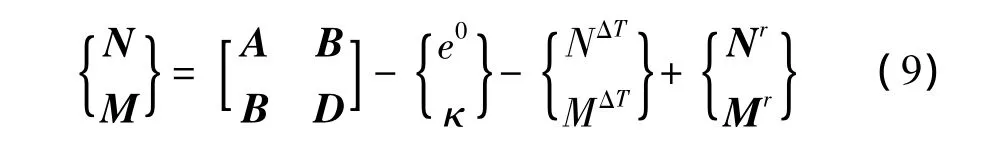
其中，e0，κ分别表示中面应变矢量和曲率矢量，NΔT，MΔT分别为基体材料热膨胀产生的力和力矩，Nr，Mr分别为SMA纤维回复时产生的力和力矩。拉伸刚度、耦合刚度和弯曲刚度矩阵A，B和D分别为:

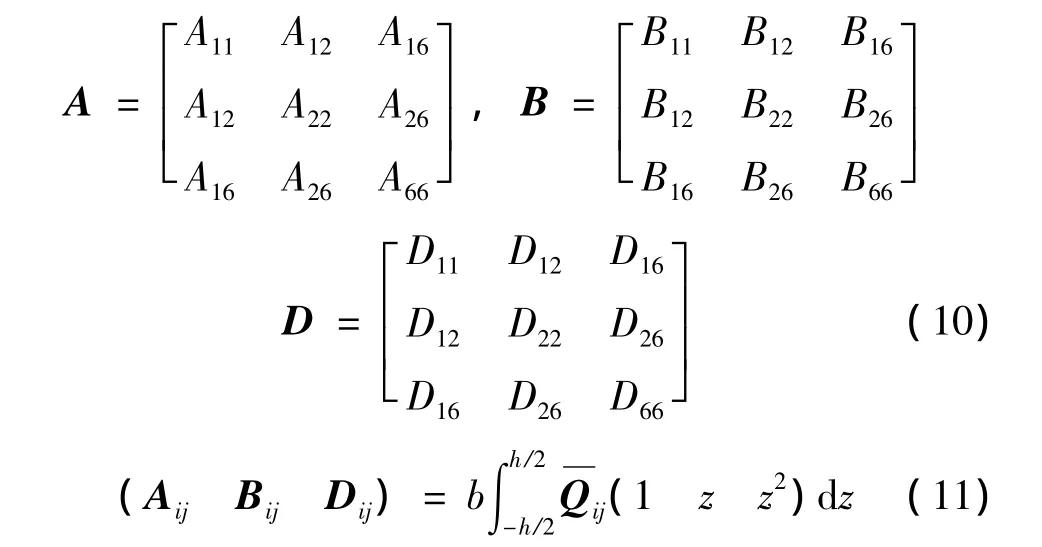
其中:b表示板簧的宽度，h=h(x)为板簧在轴向x处的厚度。若板簧关于中面对称，则Bij为0，弯曲刚度11=D11，否则 Bij不为零，弯曲刚度［9］Q是单层复合材料经转轴变换后的刚度矩阵。Nr、NΔT表述如下［2，8］:

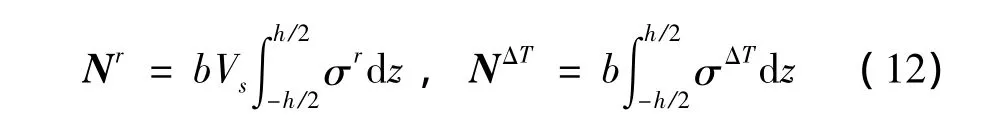
2.2 单层纤维复合材料的刚度矩阵

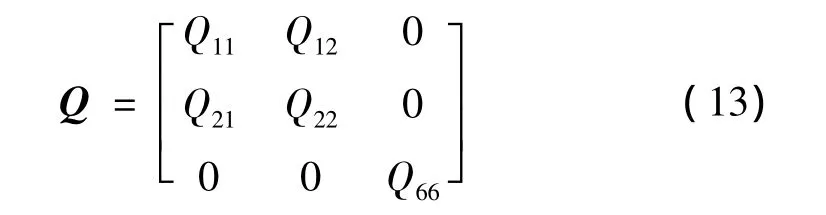
利用刚度系数与工程常数的关系［9］:

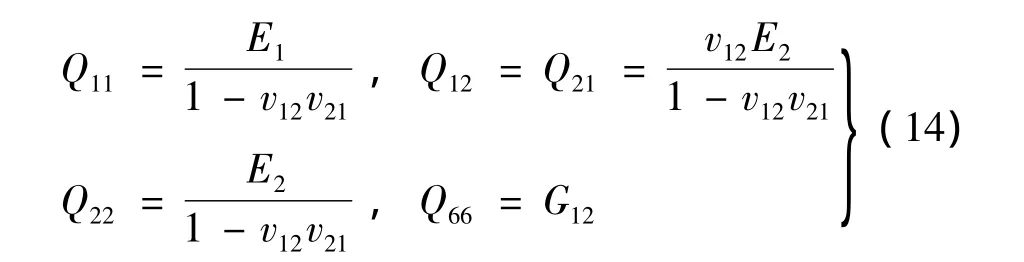
对于基体本身就是纤维增强复合材料的情形，有［8］:

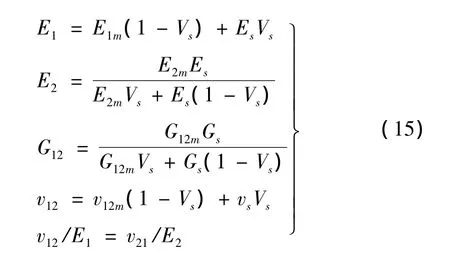
其中，下标m，s分别表示复合材料基体与SMA纤维。E，G，υ分别表示杨氏模量，剪切模量和泊松比，Vs和Vm分别为形状记忆合金与基体材料的体积比含量，Vs+Vm=1。

2.3 转轴变换

转轴变换矩阵为［9］:

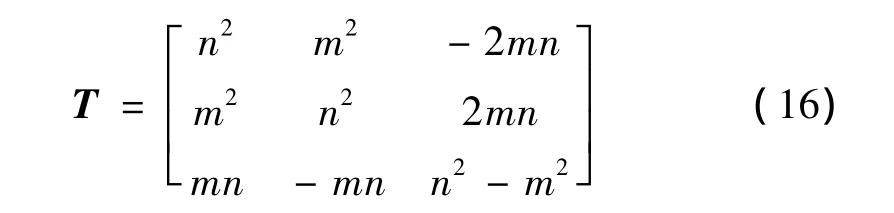
其中，n=cosθ，m=sinθ，θ为单层材料主方向与板簧轴向的夹角。利用下面的方程可以把单层纤维复合材料的刚度矩阵变换为以板簧轴向为参考坐标方向的层合材料的刚度矩阵:

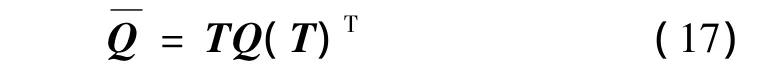
通过转轴变换将复合材料每一层的各参量转换到以板簧轴向为参考的坐标系上，极大地方便了后续的推导与计算。

2.4 温度对复合材料基体的影响

式(12)的NΔT由基体材料热膨胀产生的力，表述如下:

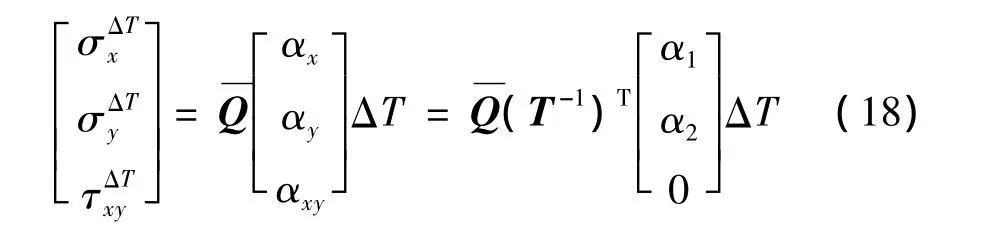
其中，α1，α2为基体材料的热膨胀系数。

3 利用瑞利—里兹法求板簧的固有频率

对于板簧，其位移边界条件为:w(0)=w(L)=0。

其变形［10］表示为:

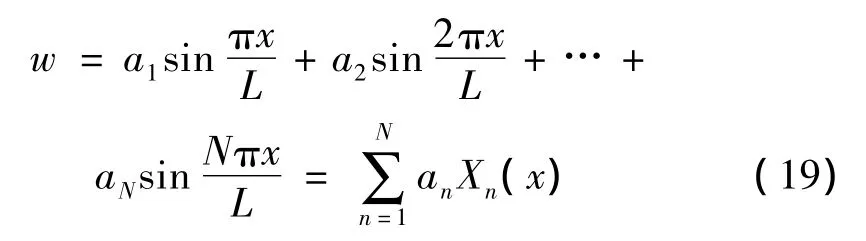
其中，a1，a2，…，aN为待定系数，显然，式(19)满足板簧的边界条件。

下面根据假定的位移函数计算板簧自由振动的总势能Π=U+V。

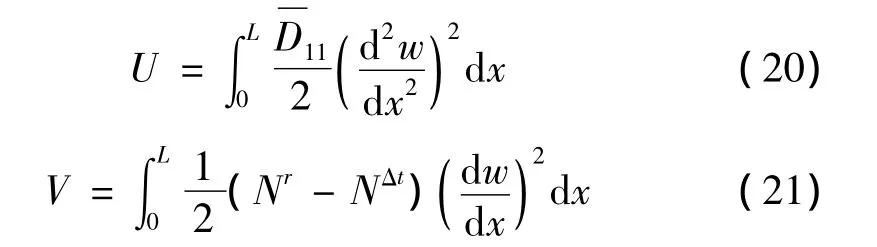
其中，U为弯曲应变能，V为SMA纤维回复力与基体材料热膨胀产生的势能［11－12］。板簧的动能为［13］:

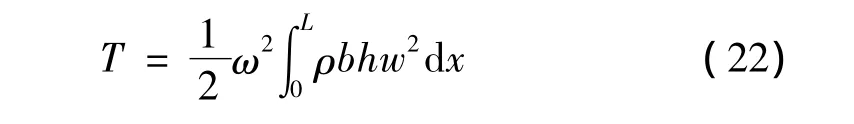
其中ρ为轴向坐标x处的板簧密度［14］:

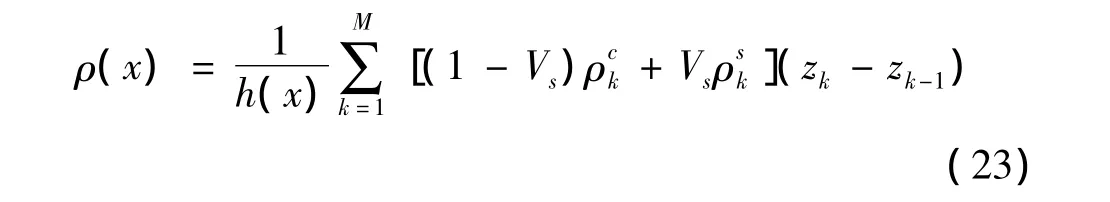
使能量为极小:

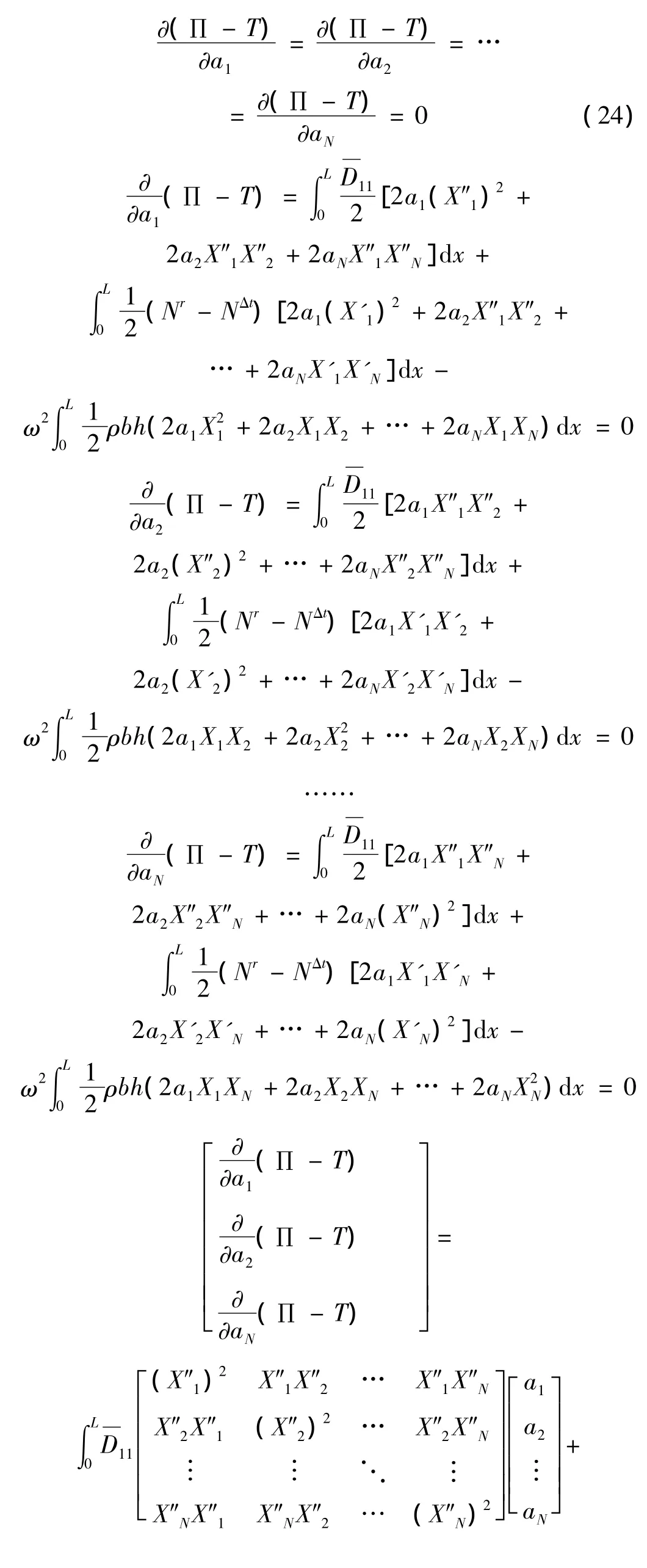
将前两项合并为广义刚度矩阵K，第三项为质量矩阵M，则上述方程可以写成下式的特征值问题:

求解方程(27)便可得到形状记忆合金变截面板簧的固有频率ω。

4 计算结果及结论分析

4.1 基本参数

表2为SMA纤维与基体材料的参数，板簧结构尺寸如图1所示［15］，共铺设20层，每层厚度1 mm。其中上面等截面部分为12层，下面变截面部分为8层，SMA纤维复合材料沿板簧轴向铺设于等截面部分，并且与石墨/环氧隔层铺设，即［θ/00/－θ］;石墨/环氧基体以［θ/－θ］的方式铺设其余各层。

根据板簧形状在x方向的对称性，取一半进行计算。对于(18)式弯曲应变能U中11的求解，要用到第(10)、(11)式，其中式(11)的h是随x而变化的，如图2所示，板簧厚度表达式为:

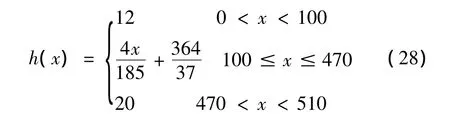
4.2 板簧固有频率随温度的变化规律

图2所示为Vs=0.5，θ=45°，位移方程取5项时板簧前三阶固有频率随温度变化的曲线。由于T＜和T＞时SMA没有发生相变，所以各阶固有频率随温度的变化不大;在奥氏体相变≤T≤和马氏体相变≤T≤时，回复应力随温度急剧变化，板簧的前三阶固有频率随温度的变化也非常明显。

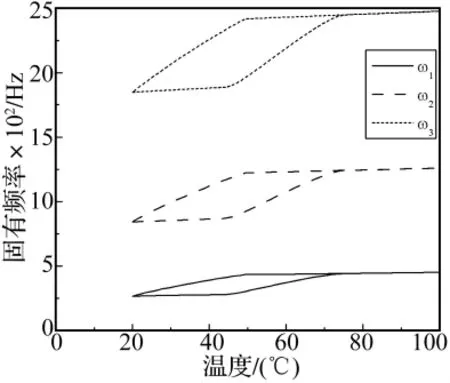
图2 板簧前三阶固有频率随温度的变化曲线(N=5)Fig.2 The first three natural frequencies curves of the leaf spring at different temperature(N=5)

为提高计算精度，同时验证板簧固有频率随(19)式截取项数增加的收敛性，在位移表达式(19)中，取不同项数计算并进行比较，结果如图3所示。由图3可知，随着项数N的增大，板簧的固有频率－温度曲线之间越来越接近，说明固有频率－温度曲线随N的增加具有收敛性。考虑到运算速度，在后面的计算中取N=5。

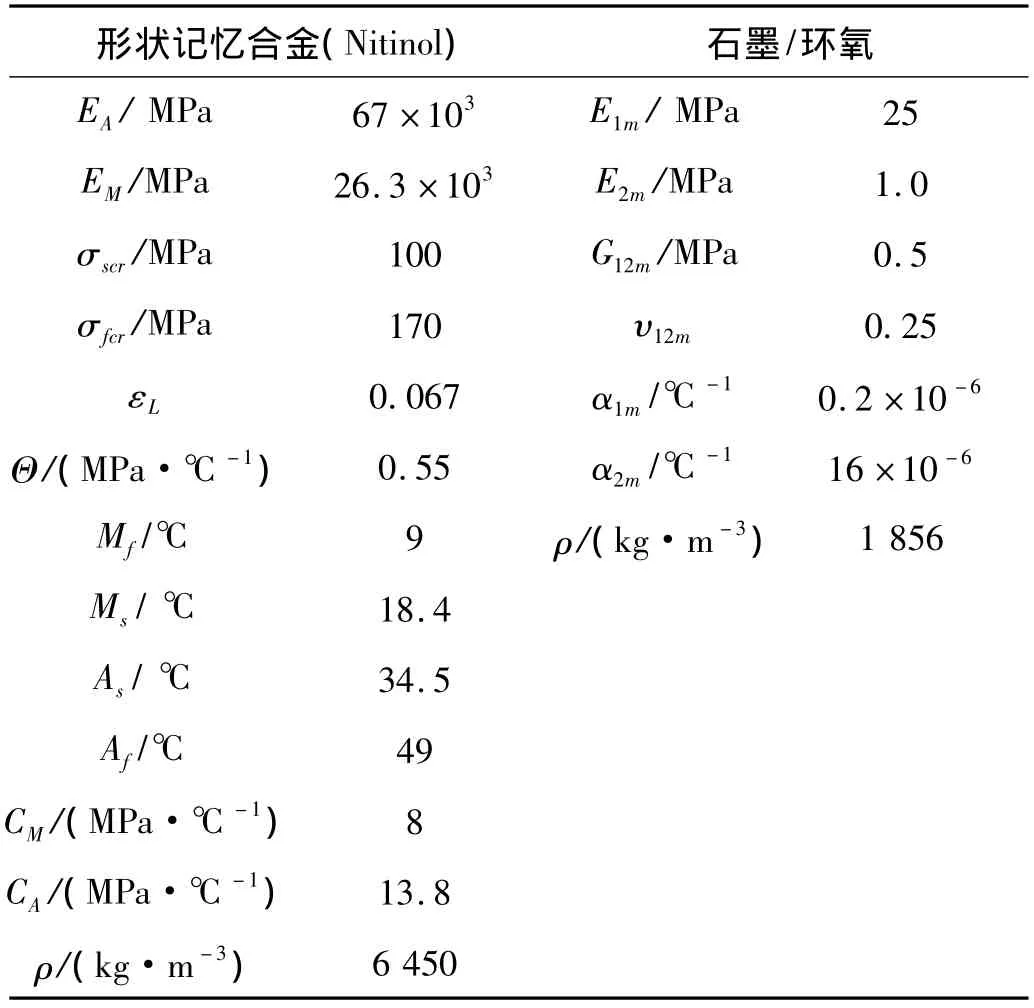
表2 材料参数表［16］Tab.2 The properties of materials［16］

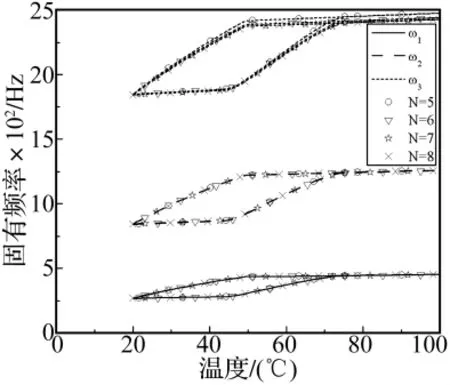
图3 瑞利－里兹法的收敛性Fig.3 Convergence of Rayleigh-Ritz method

4.3 板簧固有频率随铺层角的变化规律

图4～图6表示当SMA纤维体积含量较高的情况下(Vs=0.5)，温度分别为 30℃，60℃，80℃ (相变过程三个阶段的代表温度)时，升温过程与降温过程固有频率随铺层角度变化的曲线。板簧前三阶固有频率分别随基体材料铺层角在［0°，90°］区间的逐渐增大而减小，但变化幅度不大。图7～图9为SMA纤维体积含量较低的情况下(Vs=0.001)，温度为 30℃，60℃，80℃时固有频率随基体材料铺层角的变化曲线，可见当SMA纤维含量较低时，铺层角对板簧固有频率的影响比较明显，这与板簧的材料组分的弹性模量相对大小有关。当SMA纤维含量较大时，沿着板簧轴向铺设的SMA纤维的影响占据主导地位，因此改变基体中普通纤维的铺层角对板簧固有频率影响不大;当SMA纤维含量降低时，其影响减弱，此时基体材料对板簧固有频率的影响占据主导地位，普通纤维的铺层角对板簧固有频率的作用较为明显。值得注意的是减少SMA纤维含量，板簧的刚度随之减小，固有频率也随之降低，如图7～图9所示。另外，T＜Aσf，同温同含量的情况下，降温过程的各阶固有频率始终比升温过程的大，这是因为同温度条件下SMA的受限回复应力在降温过程比升温过程大的缘故。

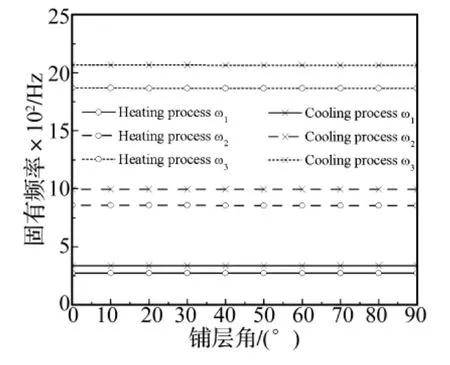
图4 30℃升温与降温过程的固有频率随铺层角的变化曲线比较(Vs=0.5)Fig.4 The natural frequencies change with ply angle during heating and cooling processes at 30℃ respectively(Vs=0.5)

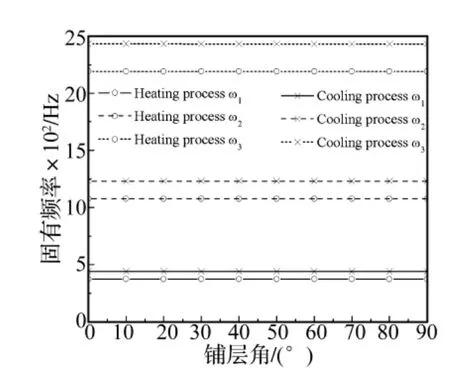
图5 60℃升温与降温过程的固有频率随铺层角的变化曲线比较(Vs=0.5)Fig.5 The natural frequencies change with ply angle during heating and cooling processes at 60℃ respectively(Vs=0.5)

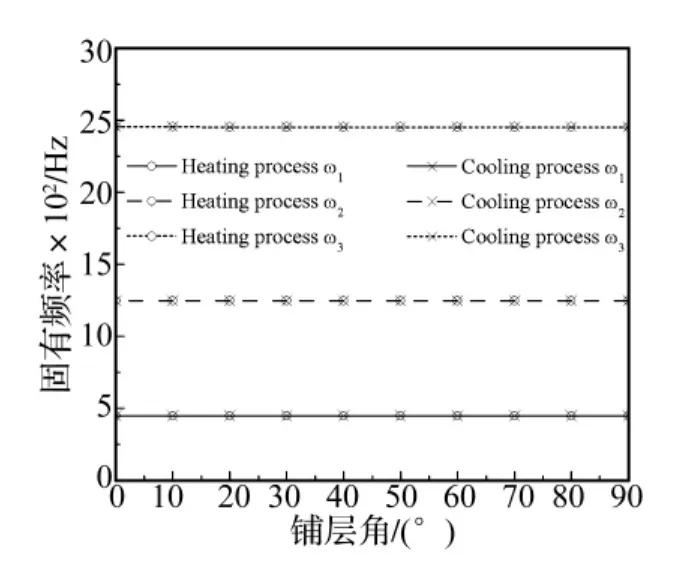
图6 80℃升温与降温过程的固有频率随铺层角的变化曲线比较(Vs=0.5)Fig.6 The natural frequencies change with ply angle during heating and cooling processes at 80℃ respectively(Vs=0.5)

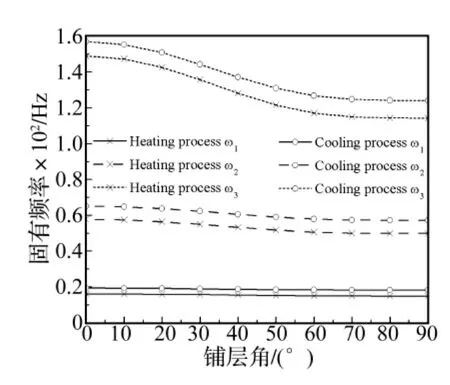
图7 30℃升温与降温过程的固有频率随铺层角的变化曲线比较(Vs=0.001)Fig.7 The natural frequencies change with ply angle during heating and cooling processes at 30℃ respectively(Vs=0.001)

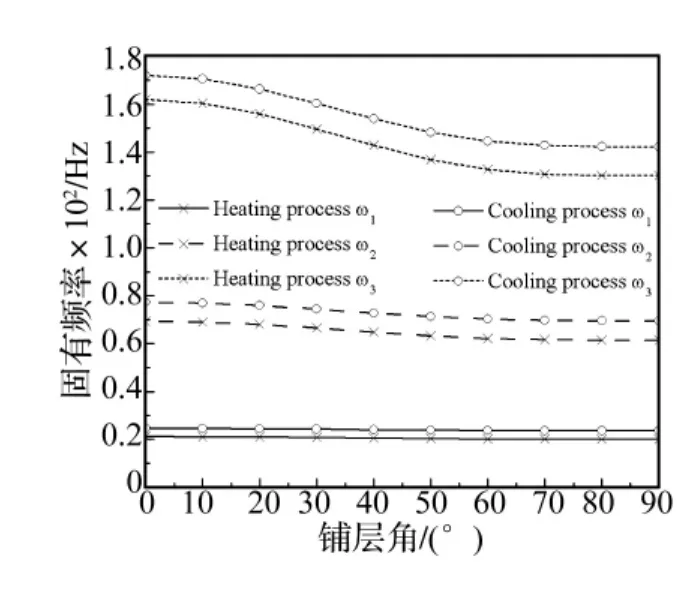
图8 60℃升温与降温过程的固有频率随铺层角的变化曲线比较(Vs=0.001)Fig.8 The natural frequencies change with ply angle during heating and cooling processes at 60℃ respectively(Vs=0.001)

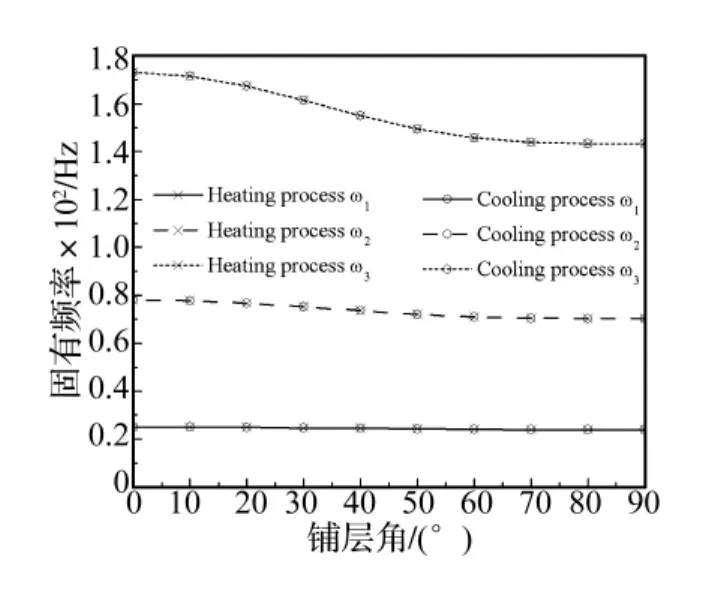
图9 80℃升温与降温过程的固有频率随铺层角的变化曲线比较(Vs=0.001)Fig.9 The natural frequencies change with ply angle during heating and cooling processes at 80℃ respectively(Vs=0.001)

4.4 板簧固有频率随SMA纤维含量的变化规律

图10～图12表示铺层角为45°时，不同的SMA纤维体积含量情况下的前三阶固有频率与温度的关系曲线。分别取 SMA 纤维含量为0.1，0.3，0.5，可见 SMA纤维含量越大，板簧的固有频率越高，在SMA相变过程的温度范围内所表现的固有频率变化幅度也越大。另外，在升温过程 T＜44.3℃和 T＞75.3℃，降温过程的T＞49.5℃时，随体积含量的增加，SMA产生的形状回复力相比基体材料产生的热膨胀力也越来越大，因此在这个温度范围内，固有频率－温度曲线随SMA纤维体积含量的变大而呈现“上翘”的现象。

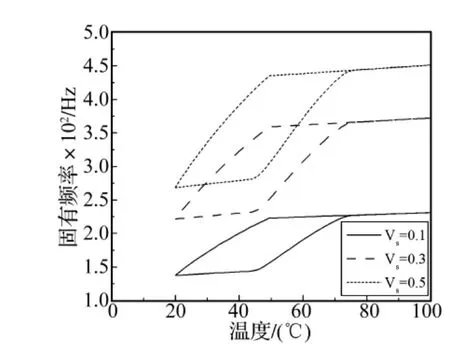
图10 不同SMA纤维含量情况下的第一阶固有频率随温度变化曲线的比较Fig.10 The contrast of the first natural frequency-temperature curves with different SMA fiber contents

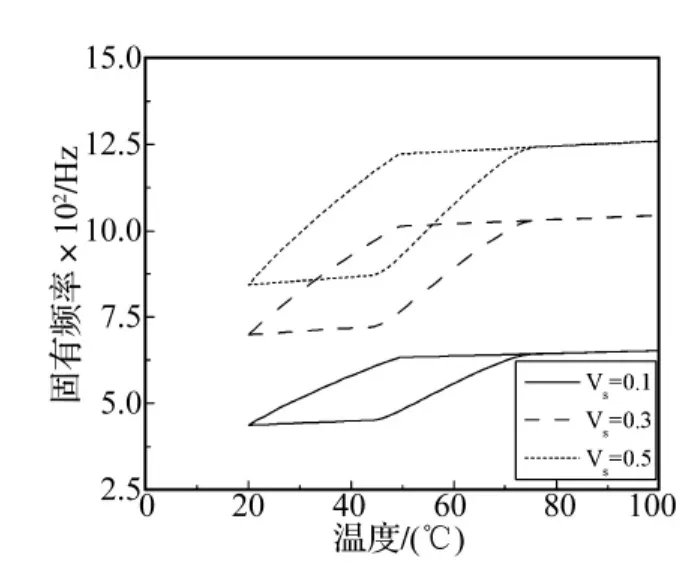
图11 不同SMA纤维含量情况下的第二阶固有频率随温度变化曲线的比较Fig.11 The contrast of the second natural frequency-temperature curves with different SMA fiber contents

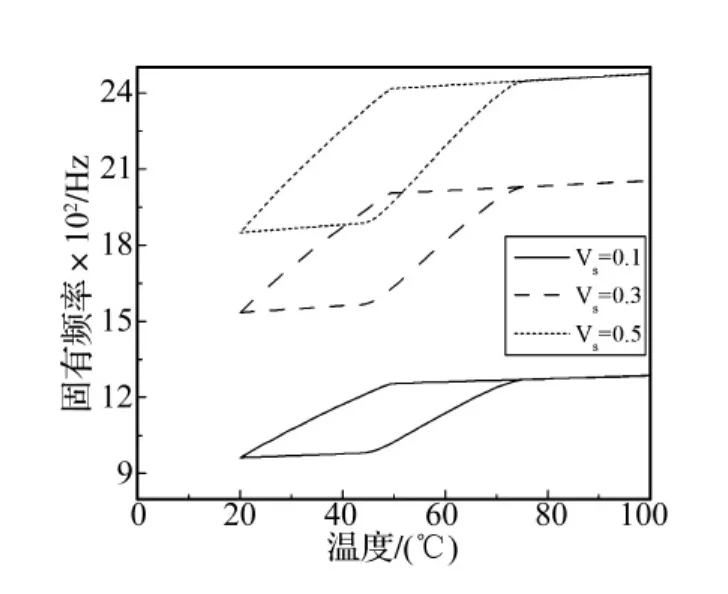
图12 不同SMA纤维含量情况下的第三阶固有频率随温度变化曲线的比较Fig.12 The contrast of the third natural frequency-temperature curves with different SMA fiber contents

4.5 板簧固有频率与铺层方式的关系探讨

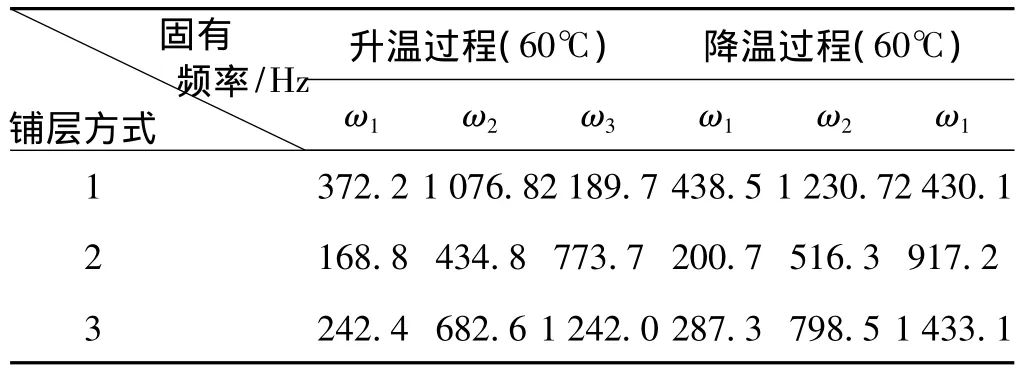
表3 不同铺层方式下的固有频率Tab.3 Natural frequency in different lay up conditions

表3是当SMA体积分数取0.5，铺层角度为45°，温度取值为60℃时，分别在升温阶段和降温阶段的三种典型铺层方式下的板簧前三阶固有频率对比。

其中:

铺层方式1:

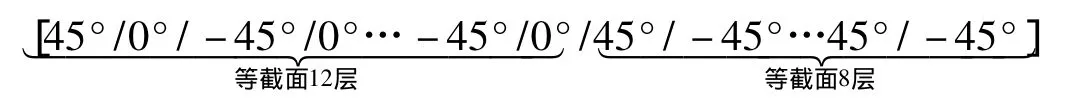
石墨/环氧层与SMA纤维复合材料层交替铺设于板簧等截面部分的12层，如图1所示。

铺层方式2:

铺层方式3:

由表中数据可知，铺层方式1的固有频率最大，其次是铺层方式3，再次是铺层方式2。原因是SMA纤维含量按照上述顺序逐步减少，所产生的形状回复力也依次减少，因此板簧的固有频率也随之依次减小。

5 结论

基于SMA的完全受限回复本构理论，复合材料结构力学理论和瑞利－里兹能量法，建立了嵌入SMA纤维的复合材料变截面板簧的力学模型，通过数值计算得到了板簧前三阶固有频率随温度的升高和降低的变化规律，以及给定温度下铺层方式和SMA纤维含量对固有频率的影响。主要结论如下:

(1)板簧的固有频率随温度的变化而变化，尤其是在SMA相变的过程中，固有频率变化更明显。可以通过改变板簧的温度，实现对其固有频率的有效调节。

(2)SMA纤维含量对板簧固有频率有重要的影响。增加SMA纤维含量可以显著提高板簧的各阶固有频率。

(3)铺层角对板簧固有频率的影响与SMA纤维含量有着密切的关系。当SMA纤维含量较低时，铺层角对板簧固有频率的影响较为明显;而当SMA纤维含量较高时，铺层角对板簧固有频率的影响不大。

(4)改变铺层方式能够显著地改变SMA纤维复合材料板簧的固有频率，从而影响对板簧固有频率的调节效果。

本文研究结果对基于SMA智能材料的半主动悬架板簧的动态设计、动力性能评估以及半主动振动控制具有一定的参考价值。

［1］任勇生，周建鹏.汽车半主动悬架技术研究综述［J］.振动与冲击，2006，25(3):162－165.

［2］李 磊，任勇生，孙爱芹，等.SMA纤维复合材料板簧刚度性能分析［J］.机械设计与研究，2008，24(3):57－61.

［3］徐晓明，任勇生，杜向红.SMA纤维复合材料变截面板簧的刚度特性研究［J］.山东科技大学学报，2011，30(1):96－102.

［4］王洪礼，沈宇航，许 佳，等.带有形状记忆合金弹簧的汽车半主动悬架随机振动的可靠性和最优控制［J］.机械工程学报，2010，46(12):93 －98.

［5］胡海岩.机械振动基础［M］.北京:北京航空航天大学出版社，2005.

［6］任勇生，王世文，李俊宝，等.形状记忆合金在结构主被动振动控制中的应用［J］.力学进展，1999，29(1):19 －33.

［7］付小华.嵌入形状记忆合金丝复合材料梁热屈曲分析［D］.兰州:兰州理工大学，2003.

［8］任勇生，孙双双.形状记忆合金纤维正交各向异性层和矩形板的非线性弯曲振动［J］.复合材料学报，2007，24(4):185－192.

［9］陈烈民，杨宝宁.复合材料的力学分析［M］.北京:中国科学技术出版社，2006:78－122.

［10］Tauchert T R，李世昌，译.结构力学能量原理［M］.北京:人民交通出版社，1984:81－86.

［11］Ro J，Baz A.Nitinol－reinforced plates:partⅢ.dynamic characteristics［J］.Composites Engineering，1995，2(1):91－106.

［12］付宝连.弹性力学中的能量原理及其应用［M］.北京:科学出版社，2004:134－138.

［13］Maheri M R，Adams R D.Modal vibration damping of anisotropic FRP laminates using the Rayleigh－Ritz energy minimization scheme［J］.Journal of sound and vibration，2003，259(1):17－29.

［14］邵 兵，任勇生.SMA纤维混杂层合梁的振动分析［J］.工程力学，2003，20(4):183－187.

［15］薛元德，徐咏梅.复合材料板簧的有限元应力分析及其设计［J］.同济大学学报，1998，26(4):393－395.

［16］Sun S S，Sun G，Han F，et al.Thermoviscoelastic analysis for a polymeric composite plate with embedded shape memory alloy wires［J］.Composite Structures，2002，58:295－302.