自适应局部独立分量分析

余成义，肖 涵，刘安中，李友荣

(武汉科技大学 冶金装备及其控制教育部重点实验室，武汉 430081)

混沌动力系统的降噪是20世纪90年代混沌时间序列分析的主要研究内容之一。由于混沌信号具有“宽频”性和“伪随机”性，如果用传统的基于频谱分析的降噪算法，会将有用信号当成噪声去掉。因此在处理混沌信号时，必须用非线性的降噪算法取代传统的线性降噪算法。

目前，Shin等［1－2］提出了基于奇异谱的降噪算法，并将该算法用于轴承、齿轮信号的降噪中，克服了传统线性降噪方法无法处理非线性数据的缺点。徐金梧等［3］将局部投影降噪用于微弱特征信号的检测中，提取设备的早期故障信号。文献［4］提出了加权相空间重构投影降噪算法，该算法采用汉宁加权窗，减少了重构误差，提高算法的效率。但上述算法主要通过主分量分析去获取数据集内总方差最大方向，与主分量分析(PCA)相比，独立分量分析(ICA)应用了数据高阶统计量，且ICA能恢复数据集内在变量的各自主要方向。为了克服全局线性ICA不适合处理非线性数据的局限性和非线性ICA需要不同约束条件的复杂性，Karhunen等［5－6］提出了局部线性ICA方法，其基本思想是先对数据进行聚类，聚类目的就是找数据的局部投影区间，再对每一个聚类进行线性 ICA。Gruber等［7］结合相空间重构给出了局部独立分量分析(本文中称其为传统局部独立分量分析)的基本模型框架。文献［8］指出该降噪算法的一些缺点:聚类中心个数人为给定和初始聚类中心随机选取导致算法的不稳定性，从而大大限制了该降噪算法的使用范围。本文在克服传统局部独立分量分析的不足的基础上提出了自适应独立分量分析降噪算法，该算法用聚集模糊K均值聚类和聚类评价函数求取高维数据集的聚类个数和聚类中心位置，具有自适应性和稳定性。

1 聚集模糊K均值聚类算法

聚集模糊K均值聚类算法［9］在传统模糊K均值聚类算法的基础上引入惩罚项，使得该算法得到的聚类结果对初始聚类中心不敏感。该算法和聚类评价函数一起使用能够确定数据集的聚类个数和聚类中心位置。

某一维信号经相空间重构后为:

X={X1，X2，…，Xn}T

其中相点 Xi=［Xi，1，Xi，2，…，Xi，m］，m 为嵌入维数或代表每个相点属性个数。用聚集模糊K均值聚类算法将数据集X聚成k类，实质求下面目标函数的最小值:

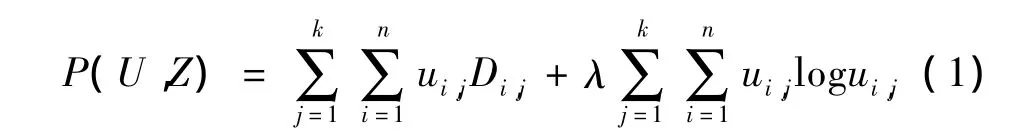
其中λ为惩罚因子，其大小决定式(1)中哪项起主要作用。

约束条件为:

式中:U为n×k的隶属度矩阵，ui，j表示第i个相点隶属于第j个聚类中心的程度。Z为包含k个聚类中心矩阵。Di，j用欧氏距离的平方来度量第i个相点与第j个聚类中心的不相似程度:

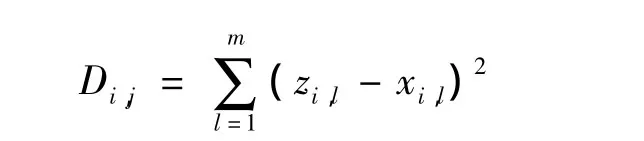
1.1 目标函数优化

可以看出式(1)是带约束的非线性优化问题。通常采用如下方法求该目标函数的最小值:先固定U，更新Z使得目标函数P最小;再固定Z，更新U使得目标函数P最小。

固定U，更新的Z由下式求得:

其中1≤j≤k，1≤l≤m，式(3)与惩罚因子 λ 无关。

固定Z，用拉格朗日乘数法将式(1)变为无约束的优化问题。更新的U由下式求得:

1.2 聚集模糊K均值聚类算法

先设置惩罚因子λ，随机选取初始聚类中心，通过交替更新Z和U，使得P(U，Z)不再变化，此时的U和Z为所求结果。由(1)式可知，优化该算法中的第一项是使数据集聚类数目增加，然而优化该算法中的第二项是使数据集聚类数目减少。算法中惩罚因子λ决定哪一项起主要作用，随着λ增加，聚类过程向着减少聚类个数方向进行，当λ增大到一定程度时，该算法就将数据集聚成了一类。λ取值合适时，聚集模糊K均值聚类算法才能准确得到真实聚类个数和聚类中心位置。下面介绍如何求取合适的惩罚因子λ。

2 聚类评价函数

文献［10］提出聚类评价函数，该算法同时考虑了各聚类内部的致密度(下式中第一项)和各聚类之间的距离(下式中第二项)。评价函数值越小，聚类效果越好。该评价函数如下:

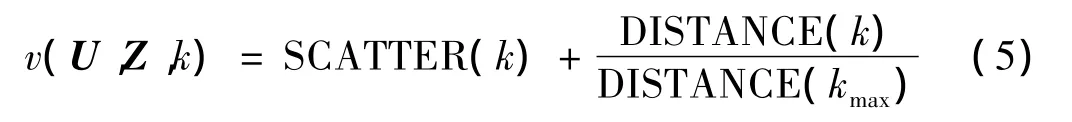
求取数据集聚类个数和聚类中心位置的算法流程如下:

该算法中包含两个循环，第一个循环是找出最小的惩罚因子λmin;第二个循环是计算最优惩罚因子值。

第一个循环的算法流程:

(1)输入初始聚类个数k，要求初始聚类个数大于真实聚类个数。

(2)设置λmin初始值为相点最大距离的0.01倍，并令t=1。

(3)运行聚集模糊K均值聚类算法，使位置相同的聚类中心聚集为一个聚类中心kt=k－kshare

(4)如果kt=k，则执行第二个循环，否则令λmin=λmin－0.1λmin，跳转到步骤(3)。

第二个循环的算法流程:

(2)如果kt=1，则该算法执行完毕，否则跳转到步骤(1)。

上述第二个循环中最小评价函数值所对应的惩罚因子即为最优惩罚因子，将其代入聚类模糊K均值聚类算法中可以得出真实的聚类个数和聚类中心位置。在有无重叠数据集上，该算法都能准确得到真实聚类个数和精确的聚类中心位置。

3 自适应局部独立分量分析算法

本文提出的改进算法主要思想是在进行传统的K均值聚类前，先使用聚集模糊K均值聚类和聚类评价函数，求出数据集的真实聚类个数和聚类中心位置，从而减少传统局部独立分量分析的参数输入，消除初始聚类中心的随机选取对该降噪算法稳定性的影响，同时提高了降噪的效果。

自适应局部独立分量分析算法流程:

(1)对一维含噪信号进行相空间重构得到轨迹矩阵X。

(2)对相空间重构后的数据去均值处理:X'=XX。对X'用聚集模糊K均值聚类和评价函数求出其真实的聚类个数k和聚类中心。

(3)对X'运用传统的K均值聚类得到k个聚类Yi。其中聚类个数和初始聚类中心为步骤(2)中求得的聚类个数和聚类中心。

(4)对每一个聚类 Yi去均值处理:Y'i=Yi－i。对每一个聚类Y'i进行独立分量分析，并由高维空间向低维空间投影，达到信噪分离的目的。其中投影阶数由最小描述长度准则来确定，得到低维数据为Li。

(5)将所得的低维数据加上第(4)步中去除的均值Y'i，并按数据原来的顺序将这k个聚类排列成完整的数据L'。

(6)将第(5)步所得到的数据L'加上第(2)步中去除的均值重构成一维数据，即为降噪后的数据。

如果噪声较大，可以重复步骤(1)～(6)，直到达到理想的效果为止。

4 仿真信号实验

Lorenz系统是典型的非线性动力系统，Lorenz信号由下式产生:

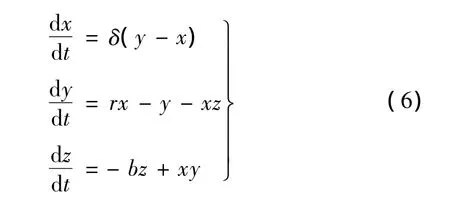
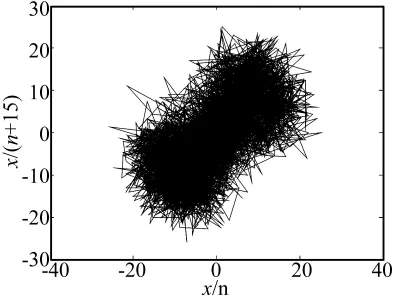
图1 降噪前信噪比为5.76 dB的Lorenz信号Fig.1 Noisy Lorenz signal waveform before noise reduction(SNR 5.76 dB)

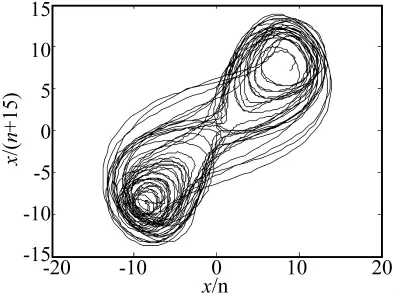
图2 降噪后信噪比为17.01 dB的Lorenz信号Fig.2 Noisy Lorenz signal waveform after noise reduction(SNR 5.76 dB)

在Lorenz信号中添加不同水平的白噪声，比较本文提出的降噪算法与传统局部独立分量分析(LICA)和全局投影(GP)降噪算法的降噪效果，如表1所示。从表1可以看出:在高信噪比的情况下，全局投影降噪的降噪效果优于LICA和本文提出的降噪算法;当信噪比较低时，LICA和本文提出的改进降噪算法的降噪效果优于GP，并且本文提出的降噪算法的降噪效果要优于LICA，同时改进算法的每次降噪效果都不变，具有很好的稳定性。

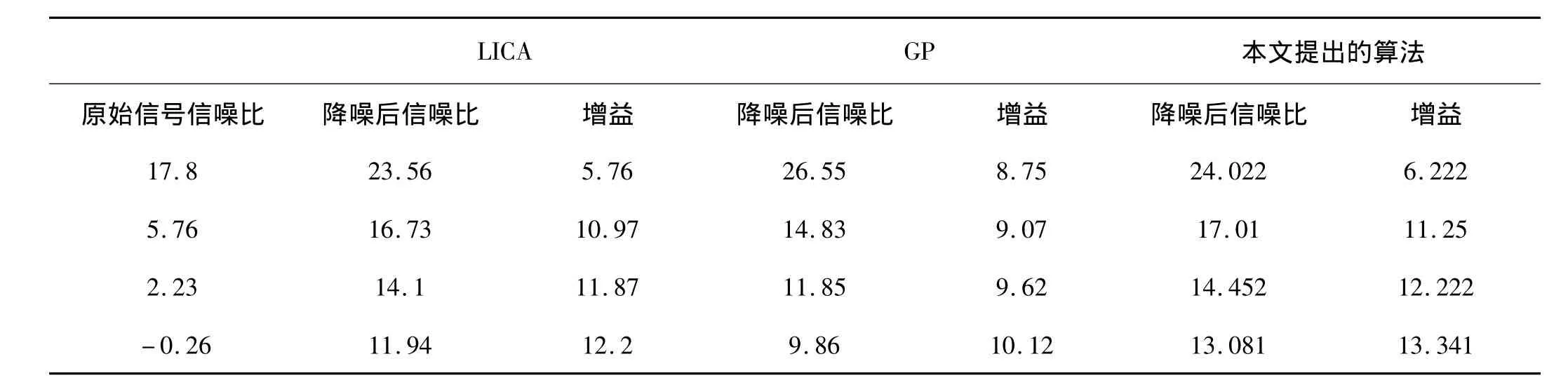
表1 几种不同的降噪算法对不同噪声水平的Lorenz信号降噪效果比较Tab.1 Comparison among the effects of several methods on Lorenz signal of different noisy level

5 自适应局部独立分量分析在齿轮箱故障诊断中的应用

试验在传动系统故障试验台上进行，减速箱为一级减速。主动齿轮为20齿，从动齿轮为37齿，输入转速为14.23 Hz，采样频率为2 000 Hz，取1 024 个数据点。主动齿轮有一个齿断裂，则主动齿轮产生的振动冲击时间间隔约为0.07 s。

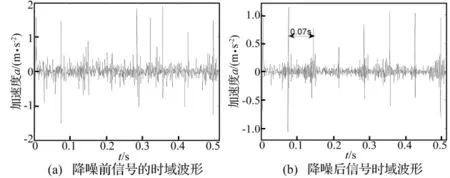
图3 原始信号及降噪信号Fig.3 The original signal and the signal after noise reduction

图3(a)为减速箱振动信号的时域波形，从时域图中很难看出周期性的冲击信号;图3(b)为采用本文降噪算法处理后的信号。从降噪后的信号时域图中，可以明显的看出周期冲击，且冲击间隔为0.07 s。说明本文提出的降噪算法能有效地提取断齿故障信号中冲击成分。

6 结论

(1)与传统的局部独立分量分析相比，本文提出自适应局部独立分量分析降噪算法，减少了输入参数(聚类中心数目)，克服了由于传统K均值聚类导致的降噪效果的不稳定性。将该算法应用到含噪Lorenz信号和含有噪声的齿轮冲击信号中，都能得到比较好的降噪效果。

(2)噪声较大时，可以采取多次循环的方法来逐步消除噪声，在刚开始循环中，嵌入维数应取大一些，噪声变小时，嵌入维数取小些，但必须满足嵌入定理。

［1］Shin K，Hammond J K，White P R.Iterative SVD method for noise reduction of low-dime-nsional chaotic time series［J］.Mechanical Sys-tem and Signal processing，1999，13(1):115－124.

［2］吕志民，张武军，徐金梧.基于奇异谱的降噪方法及其在故障诊断技术中的应用［J］.机械工程学报，1999，35(3):95－99.

［3］徐金梧，吕 勇，王海峰.局部投影降噪算法及其在非线性时间序列分析中的应用［J］.机械工程学报，2003，39(9):146－150.

［4］吕 勇，李友荣，肖 涵，等.基于加权相空间重构降噪及样本熵的齿轮故障分类［J］.振动工程学报，2009，22(5):462－466.

［5］Karhunen J， Malaroiu S. Locally linearind-ependent component analysis［C］.Proceedin-gs of the International Joint Conference on Neural Networks，1999，2:882－887.

［6］Karhunen J， Malaroiu S. Local linear inde-pendent component analysis using clustering［J］.Int.Journal of Neural Systems，2000，10(6):439 －451.

［7］Gruber P，Stadlthanner K.Denoising using local projective subspace methods［J］.Neuroc-omputing，2006，69(13 －15):1485－1501.

［8］肖 涵.基于高斯混合模型与子空间技术的故障识别研究［D］.武汉:武汉科技大学，2007.

［9］Li M J，Ng M K.Agglomerative fuzzy K-mea-ns clustering algorithm with selection of number of clusters［J］.IEEE Transactions on Knowledge and Data Engineering，2008，20(11):1519－1534.

［10］Sun H，Wang S.FCM-based model selection algorithms for determining the number of clusters［J］.Pattern Recognition，2004，37(10):2027－2037.