改进的复杂噪声源识别方法

余桐奎

(大连测控技术研究所，大连 116013)

水声隐身性是水下航行器最主要的性能之一。如何通过检测航行器的振动和噪声信号，有效估计各噪声源对辐射噪声的贡献大小，从而有效识别主要噪声源是一个十分重要的问题。为了解决这一问题，国内外对此进行了大量的研究，并提出了许多用于主要噪声源识别的方法。尽管如此，在实际工程中，由于水下航行器各声源的频率结构的复杂性、声源之间的相互干扰及传递路径的千差万别等问题，都使得主要噪声源识别问题很难得到合理解决。基于此原因，本文提出了基于相干功率谱的层次分析法和基于偏相干［1］的层次分析法，并给出了仿真研究结果及工程应用结果。

1 断矩阵构建新方法及偏差修正

层次分析法［2－3］的关键是判断矩阵的建立，判断矩阵中各元素是根据两两比较法和1～9标度法确定的，但是，准确构造出判断矩阵是难点，这也是传统层次分析法的一个较大缺陷，因此，有人提出了灰色层次分析法和模糊层次分析法，这些方法相对比较繁琐，在噪声源分析的实际应用中不是很适合，感兴趣者可参考文献［14］。本文在原有两两比较法的基础上提出一种新的构建判断矩阵的方法，具体步骤如下:

第一步:对与本层次相关的元素，分别与评价点噪声作相关分析，根据它们的相关程度进行排序。

第二步:根据1～9标度法对相干程度最大的元素重要程度定位取值，再依次对其他元素定位取值。

第三步:用各元素的排序值两两相减后加1的原则，来确定各元素在判断矩阵中的值。这里加1原则是通过大量计算、检验基础上提出的，加2、加3理论上也可以，但是具体准确性如何还未作验算，有兴趣者可以自行验算。

这一思路还是比较清晰的，各层元素相互间关系的确定相对也比较准确，而且，相对于两两比较法计算量也没有增加。从目前所有仿真及试验数据处理结果来看，构造判断矩阵的成功率为100%。但是，并不等于这种构建方法完全有效，如果出现构造的判断矩阵不符合一致性检验条件，则需要对判断矩阵进行修正，这里主要介绍两种经过检验的简便、有效的偏差修正方法［5］。

(1)偏差最大项修改法

根据判断矩阵A的排序权向量W=［w1，w2，…，wn］T，重新构造一个判断矩阵A*=(a·ij)=(wi/wj)计算偏差矩阵:

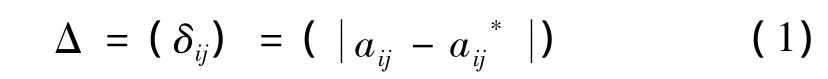
其中δij最大项对应的aij进行修正:

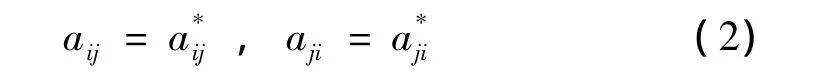
将式(2)代入原矩阵A，形成新的判断矩阵。这里需要注意的是，并不一定是将最大项的原值代入原矩阵A，需要结合各声源(或振源)与评价点之间的相干函数及相关的频谱分析来确定，这样判断矩阵的一致性可以得到明显改善，若仍不能满足一致性检验，则按上述操作，逐步调整，直到满足要求。

(2)偏差平方和最大行修改法

与(1)同样的方法构造判断矩阵A*，计算矩阵Δ后，再计算:

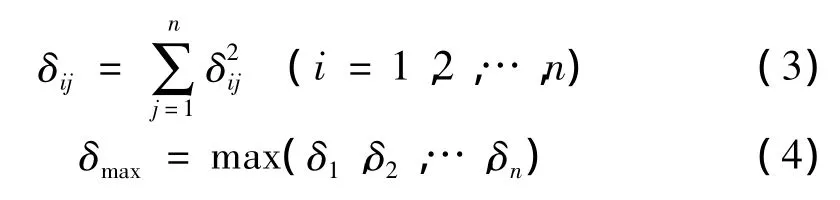
根据δmax所在行k，修正判断矩阵A令:

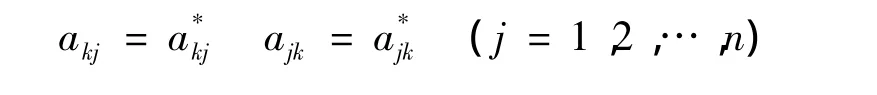
2 仿真研究

仿真条件:仿真模型如图1所示，x1(t)，x2(t)，x3(t)，x4(t)分别作为输入信号，输出信号y(t)，输入到输出的频率响应函数 h1(t)，h2(t)，h3(t)，h4(t)均为1，n(t)为高斯白噪声，采样频率为4 096 Hz，时间长度为 0.5 s。

其中:f1=10 Hz，f2=60 Hz，f3=35 Hz，f4=85 Hz，f5=70 Hz，f6=100 Hz，φ1，φ2，φ3，φ4，φ5，φ6，φ7，φ8是以 φ =rand［1，length(1，t)］的随机相位出现。

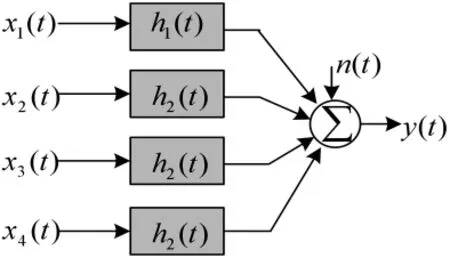
图1 多输入/输出模型Fig.1 Multiple input/output model

2.1 基于相干分析的层次分析法

根据层次分析原理［6－7］，建立层次结构图如下所示:

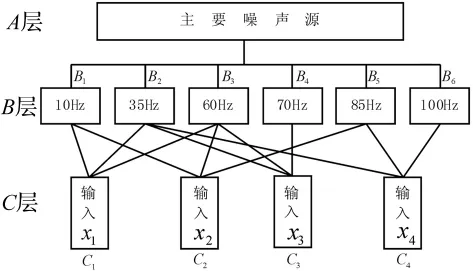
图2 噪声源层次分析结构图Fig.2 AHP model for noise source

对于A－B层的判断矩阵，应根据评价点处噪声较大的各频带或者峰值频率所对应的声压级的大小，并考虑 计权的影响后，按1～9标度法确定，如表1所示:

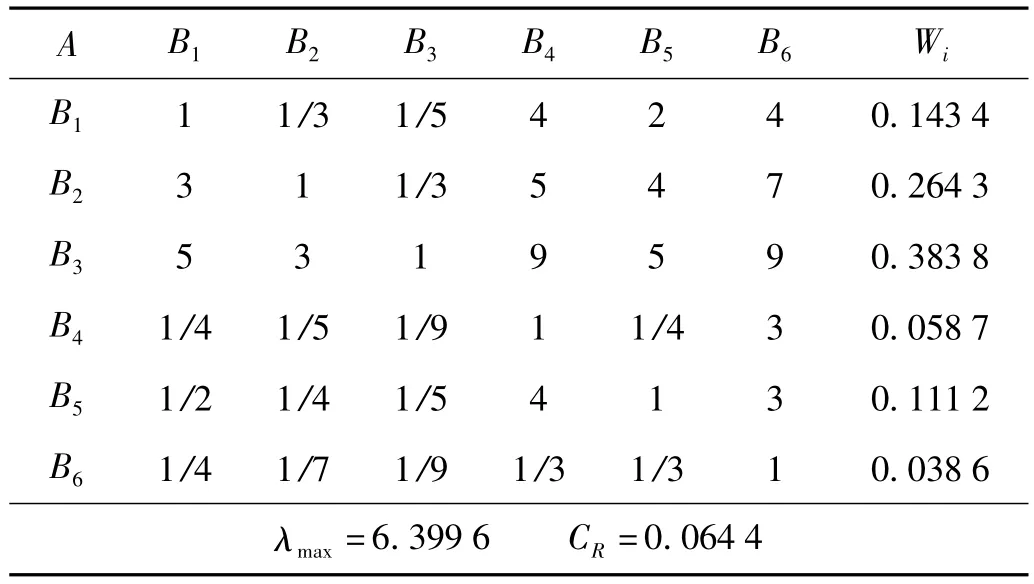
表1 目标层与频率层的判断矩阵Tab.1 Pair-wise comparison matrix

根据C1～C4四个声源信号与评价点y噪声相干函数值的大小和层次分析图，采用1～9标度法可构造B～C层的判断矩阵。由于仿真条件理想化，B～C层判断矩阵内元素均由1构成，因此，总的排序结果如表2所示。

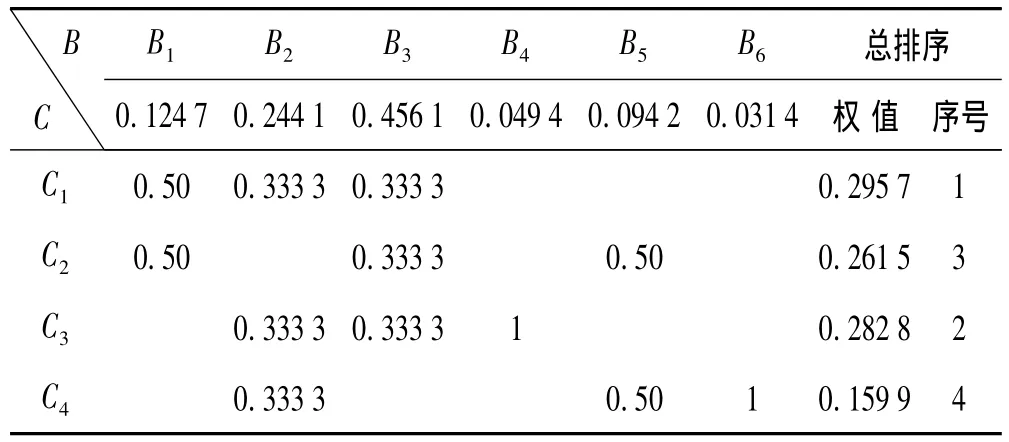
表2 噪声源识别总的排序结果Tab.2 Priority matrix for noise source identi fication

由表2分析可得:评价点处频率为10 Hz噪声主要来自于输入x1，x2;评价点处频率为35 Hz噪声主要来自于输入x1，x3，x4;评价点处频率为60 Hz噪声主要来自于输入x1，x2，x3;评价点处频率为70 Hz噪声主要来自于输入x3;评价点处频率为85 Hz噪声主要来自于输入x2，x4;评价点处频率为100 Hz噪声主要来自于输入x4。总之，x1对评价点噪声贡献最大，x3次之，x2略小于x3，x4贡献最小。

2.2 基于偏相干分析的层次分析法

仿真条件与2.1相同，唯一不同的是B～C层的判断矩阵的建立变为基于偏相干函数的大小构建的，根据C1～C4四个声源信号与评价点y噪声偏相干函数值的大小和层次分析图2，采用1～9标度法可构造B～C层的判断矩阵，具体结果如表3～表6所示，总的排序结果见表7。

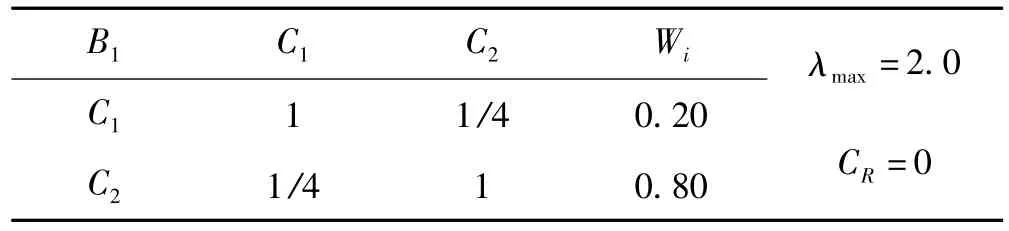
表3 频率层B1因素与声源层的判断矩阵Tab.3 Pair-wise comparison matrix for the belt B1

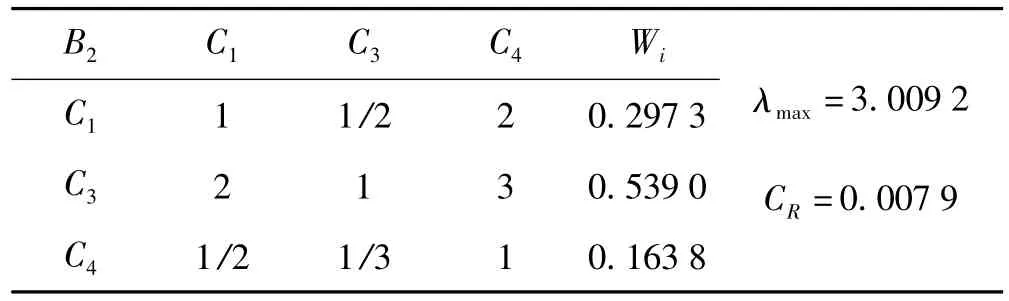
表4 频率层B2因素与声源层的判断矩阵Tab.4 Pair-wise comparison matrix for the belt B2

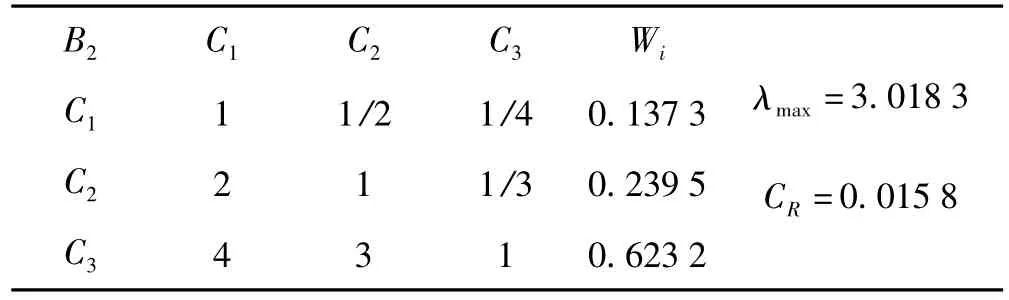
表5 频率层B3因素与声源层的判断矩阵Tab.5 Pair-wise comparison matrix for the belt B3

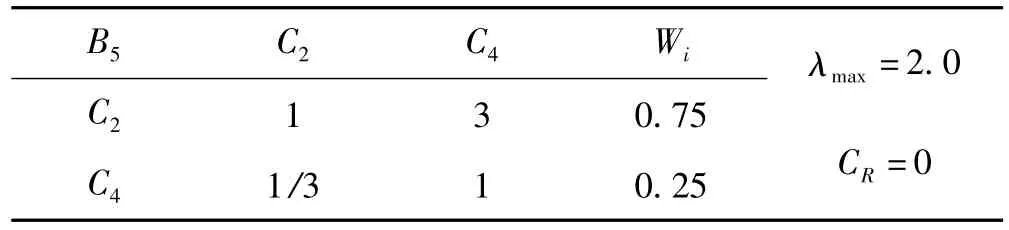
表6 频率层B5因素与声源层的判断矩阵Tab.6 Pair-wise comparison matrix for the belt B5

依据上述判断矩阵及权值分配，可得噪声源识别总的排序计算结果如表7所示。

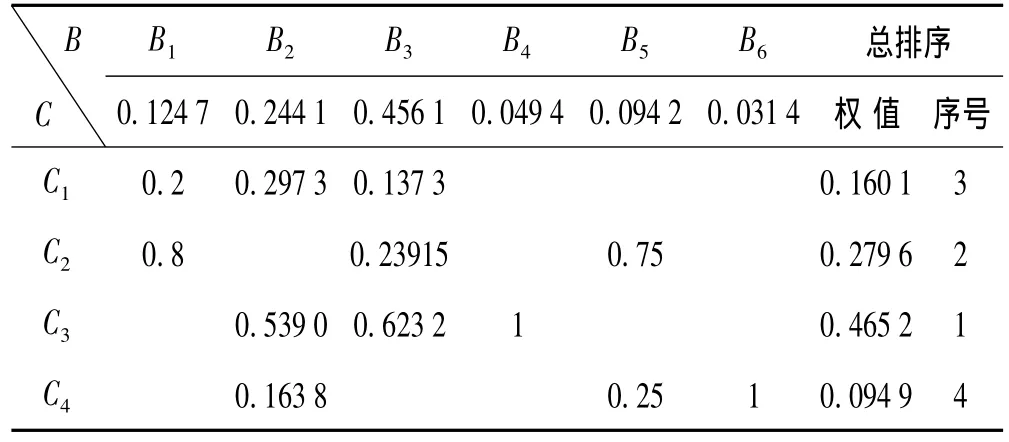
表7 噪声源识别总的排序结果Tab.7 Priority matrix for noise source identification

由表7可看出，评价点处频率为10 Hz噪声主要来自于输入x1，x2，其中x2的贡献最大;评价点处频率为35 Hz噪声主要来自于输入x1，x3，x4，其中x3贡献值大于x1和x4，x1略大于x4;评价点处频率为60 Hz噪声主要来自于输入 x1，x2，x3，其中 x3贡献值大于 x1和 x2，x2略大于x1;评价点处频率为70 Hz噪声主要来自于输入x3;评价点处频率为85 Hz噪声主要来自于输入x2，x4，其中x2贡献值大于x4;评价点处频率为10 Hz噪声主要来自于输入x4。总之，x1对评价点噪声贡献最大，x3次之，x2略小于x3，x4贡献最小。

由表3可看出，各频率层与声源层关系非常模糊，这是由于相干分析在解决多源相干性问题时自身固有缺陷所致;而由表7可清楚看出各频率层与声源层关系。因此，在解决噪声源具有强相干性的多源系统识别问题时，基于偏相干分析噪声源层次分析法是具有一定优势的。

3 试验研究

为了检验上述方法在复杂噪声源识别应用中的可行性，开展了实船主机机械系统振动与噪声测试试验研究。湖试水深约30 m，被测船用主机为上海柴油机CA－6135，试验主要测量主机基座上下部位、变速箱、汽缸、电机、高压油泵、排气管和水泵上下部位的纵向振动及主机水声场辐射噪声。

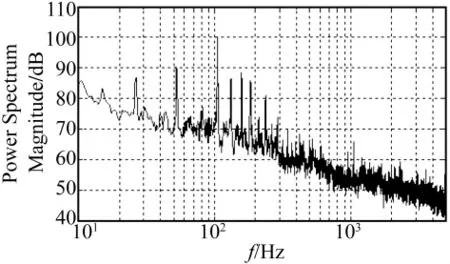
图3 主机噪声频谱图Fig.3 Flat spectrum of marine host noise

由图3可以看出，主机噪声低频线谱非常丰富，根据层次分析理论的步骤，尽量以主要峰值频率作为评价目标，从而构建出复杂声源诊断结构图。由于主机辐射噪声线谱谐波分量很多，所以，在MATLAB中进行运算时采用了最小二乘拟合的方法，门限设置为8 dB，从而简化了谱线峰值频率选取过程，具体如图4所示。

根据上述测量结果及分析，依据判断矩阵的建立方法，建立目标层A与频率层B、频率层B与各因素与声源层C中相应元素之间的判断矩阵。

对于A－B层的判断矩阵，应根据评价点处噪声较大的各频带所对应的声压级的大小，并考虑A计权的影响后，按1～9标注法确定，具体如表8所示。

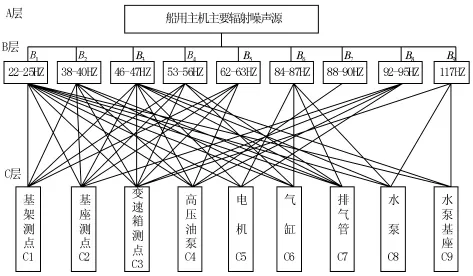
图4 主机层次分析结构图Fig.4 AHP model for marine host noise source

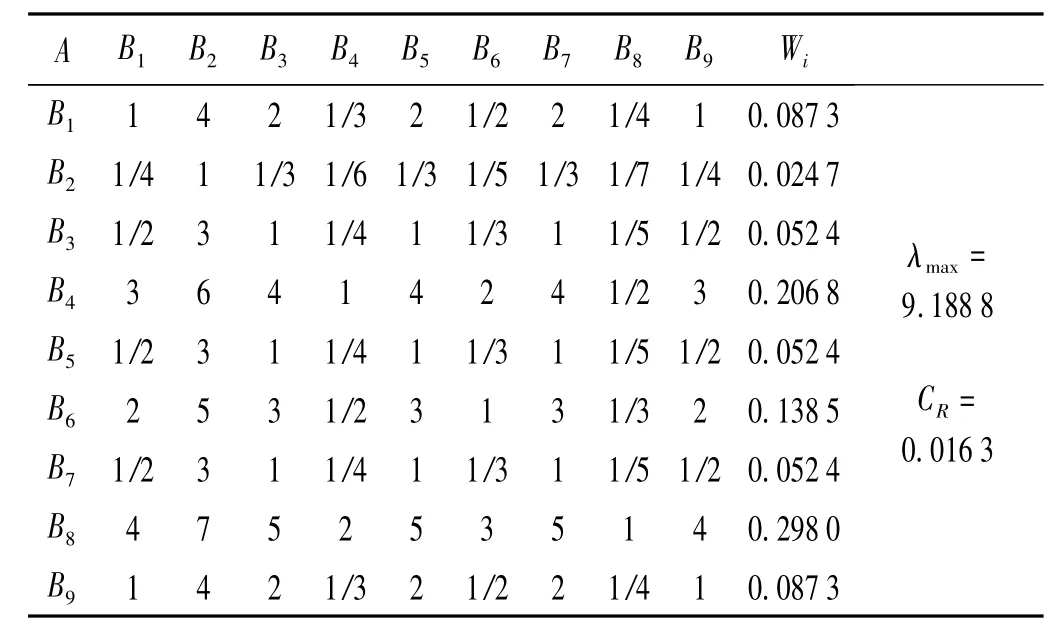
表8 目标层与频率层的判断矩阵Tab.8 Pair-wise comparison matrix

根据C1～C9振动信号与评价点辐射噪声偏相干值的大小和层次分析图，采用1～9标度法可构造B～C层的判断矩阵，以B1因素为例，如表9所示，其余B2～B9评价因素以此相同原则构建，这里不再列出。

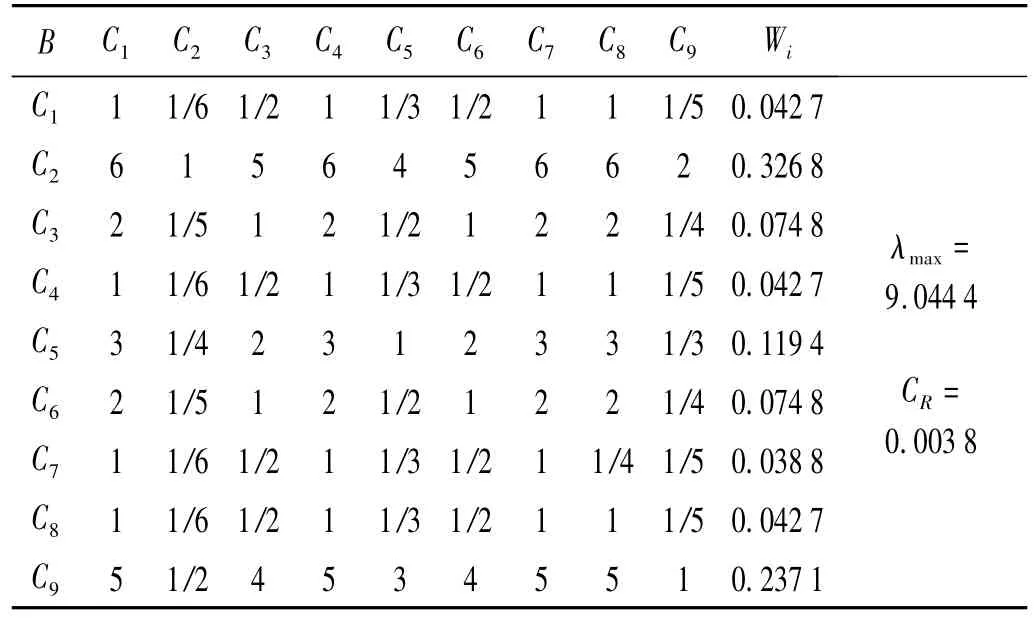
表9 频率层B1因素与声源层的判断矩阵Tab.9 Pair-wise comparison matrix for the belt B1

根据上述各判断矩阵及其权值分配，噪声源总排序结果，如表10所示。

由表10并结合主机振动特征分析可得:

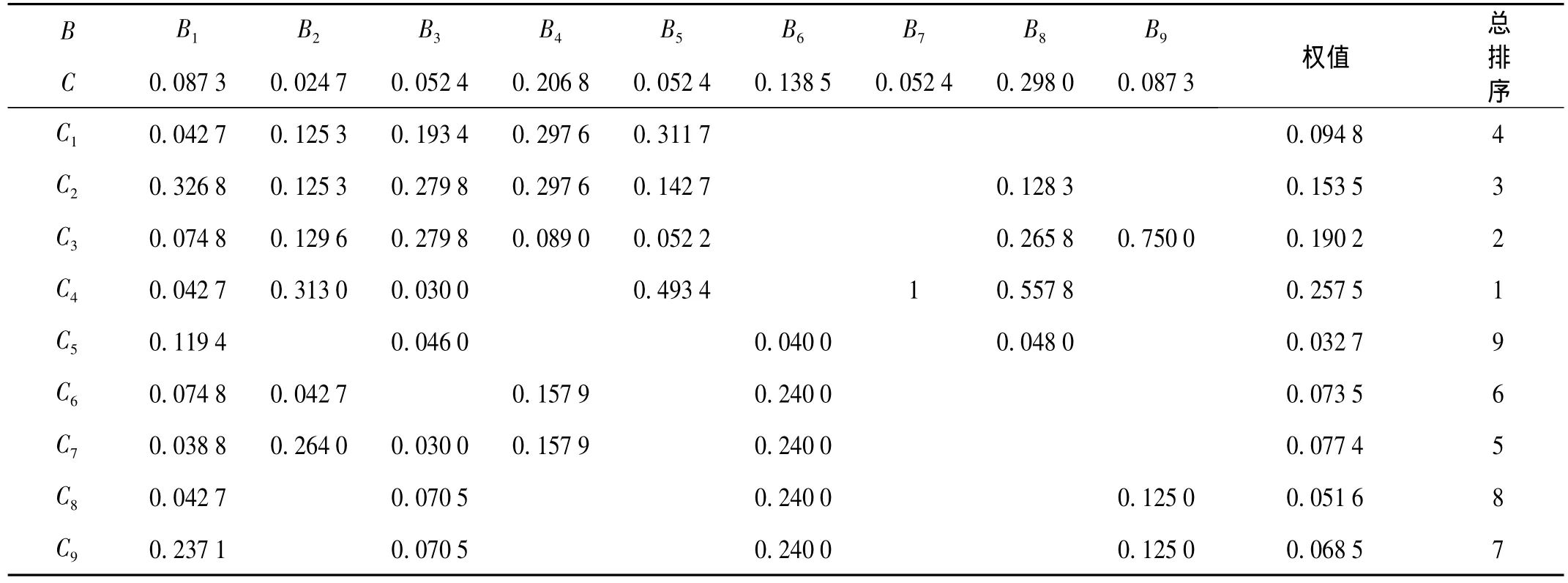
表10 噪声源总排序结果Tab.10 Priority matrix for noise source identification

(1)各频段的噪声来源并不相同，主机不同部分对不同频段具有不同的贡献程度。对于22～25 Hz频段的噪声，所有振动测点都有，说明这一频段噪声是主机的三次谐波频率激励船体辐射较强噪声;对于46～47 Hz频段的噪声，是主机的六次谐波频率激励船体辐射噪声。

(2)30～32 Hz频段主要来自于主机基架和变速箱;38～40 Hz主要与主机基架、基座、变速箱、高压油泵、气缸及排气管有关;53～56 Hz主要与主机基架、基座、变速箱、气缸及排气管有关;62～63 Hz频段主要与主机基架、基座、变速箱及高压油泵有关;84～87 Hz频段主要与电机、气缸、排气管及水泵有关，是主机的11倍频共振;88～90 Hz频段来自于高压油泵，由于高压油泵与主机相连的飞轮在主机内部，无法计算它的基频，所以，这里无法判断是高压油泵的多少次谐波频率。对于92～95 Hz频段主要来自于主机基座、变速箱、高压油泵和电机，由主机12倍频共振产生的。

4 结论

基于噪声源层次分析结构图，给出了具体层次分析流程;对于判断矩阵构建问题，在两两比较法的基础上提出了一种新的判断矩阵构建方法，实践证明该方法可以提高判断矩阵构建速度和精度;建立了基于相干函数和偏相干函数的噪声源层次分析方法，通过仿真计算和对比分析，发现基于偏相干函数的噪声源层次分析方法可解决多源系统中具有强相干性的噪声源识别问题，优于基于相干功率谱分析的层次分析法。通过对实船主机振动与噪声的综合测试，应用偏相干理论和层次诊断法对主机系统的主要噪声源进行了综合分析，结果表明，基于偏相干分析噪声源层次分析法用于复杂噪声源识别与排序是可行的。

［1］贝达特J S，皮尔索 A G，凌福根译.相关分析和谱分析的过程应用(第1版)［M］.北京:国防工业出版社，1983.

［2］Saaty T L.The analytic hierarchy process［M］.New York:Mc Graw-Hill，1989:32 －35.

［3］赵焕臣.层次分析法［M］.北京:科学出版社，1986.

［4］郭齐胜，董志明，李 亮，等.系统建模与仿真(第1版)［M］.北京:国防工业出版社，2007.

［5］王应明.判断矩阵排序方法综述［J］.管理科学学报，1995(3):101－114.

［6］黄其柏.复杂噪声源层次诊断方法及其在风机中应用研究［J］.分机技术，1997(6):13－16.

［7］Shu G Q，Liang X Y.Identification of complex diesel engine noise sources based on coherent power spectrum analysis［J］.Mechanical Systems and Signal Processing，2007，21:405－416.