运用内积相关性结合迭代相减识别两点声源

寇海亮，冒凯炫，赵晓丹

（江苏大学 汽车与交通工程学院，江苏 镇江 212013）

运用内积相关性结合迭代相减识别两点声源

寇海亮，冒凯炫，赵晓丹

（江苏大学 汽车与交通工程学院，江苏 镇江 212013）

提出运用内积相关性识别两点声源的新方法，通过在声源面上构造虚拟声源，计算虚拟声源在传声器阵列上的声压，构造虚拟声源的声压向量，将其归一化，与传声器实际测得的声压信号作内积运算，通过优化算法搜索内积模的极值，当内积模达到最大值时，根据内积相关性原理，识别出目标声源的位置。当声源间距离较近时，声源识别精度受到声源间的干扰影响，引入迭代循环算法降低声源相互干扰的影响，以传声器测量面上剩余的声压作为判断循环终止的条件。计算结果表明，利用内积相关性结合迭代循环相减算法能有效识别出两点声源。

声学；声源识别；内积；迭代相减；传声器阵列

随着计算机技术水平和现代数字信号处理技术的不断进步，基于阵列信号处理的声源识别技术取得了很大的发展［1］，其中近场声全息技术（NAH）［2］和波束形成（Beam-forming）［3］是两种常用方法。近场声全息技术主要用于近距离和中低频的声源识别［4-5］。波束形成法是通过计算选定方向上的声波辐射能量的相对大小来判断波的入射方向［6-7］，该方法在聚焦声源平面上各位置时，根据不同传声器与参考点之间接收信号的时间差，对阵列接收到的信号进行相位延时再求和输出，进而提取不同方向声音的相对强度，其基本原理可归结为“延时求和”。

工程实际中的噪声源大多是由多个子声源组成的分布式声源，对于多点分布声源的识别定位具有现实意义。本文基于球面波模型，提出利用内积相关性识别两点声源的方法［8］。该方法不需要计算不同传声器之间的时间延时，通过在声源面上构造虚拟声源，计算目标声源的声压向量与虚拟声源声压向量的内积，利用内积相关性原理来识别声源位置。识别多点声源的难点在于相近声源之间的相互干扰，使得声源识别的结果不理想。本文结合迭代循环相减算法解决两点声源间相互干扰的问题，计算结果验证了该方法的识别效果。

1　两点声源识别原理

本文以两个点声源的辐射模型为研究对象来描述声源识别的过程。假设声源面上两个点声源S1和S2向外辐射的声波满足叠加原理：即在同一空间中某一点处接收的声压等于两个声源单独产生的声压的代数和。采用一组m×n等间距的阵列测量声压信号，位于第i行、第j列传声器（i=1，…，m；j=1，…，n）的坐标用（xi，yj）表示，声源面与阵列面的距离为d；两个声源具有相同的频率ω，对应的波数为k；声源S1的坐标为（x1，y1），声源强度为q1，初相位为φ1；声源S2的坐标为（x2，y2），强度和初相位分别为q2和φ2；阵列面上的传声器接收的时域声压信号p（t）可表示为

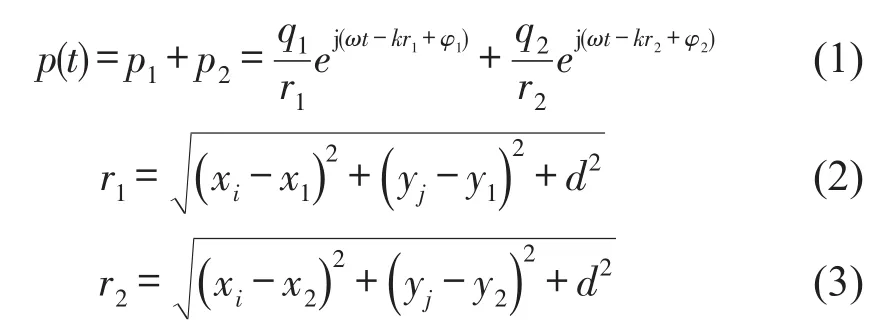
将传声器测得的声压信号经傅里叶变换，并按阵列的位置顺序整合成声压向量P，向量P可表示为

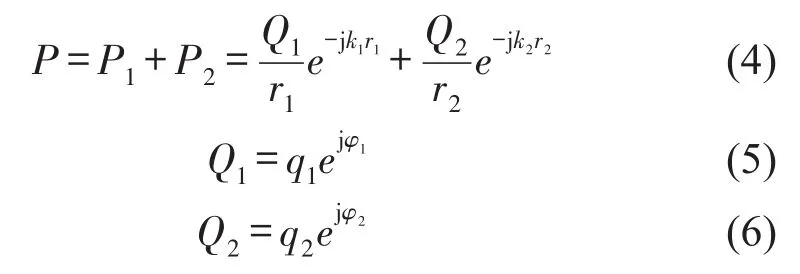
其中P1和P2分别为声源S1和声源S2辐射的频域声压向量，r1表示声源S1与阵列上的各个传声器之间的距离向量，r2表示声源S2与阵列上各个传声器之间的距离向量，Q1、Q2分别为复数的声源强度。在声源面上以估计的频率ω构造一个虚拟声源，虚拟声源位置用（xν、yν）表示，虚拟声源辐射到阵列上的声压信号按照同样的阵列位置顺序整合成虚拟声源向量，并进行归一化处理后得到基向量e

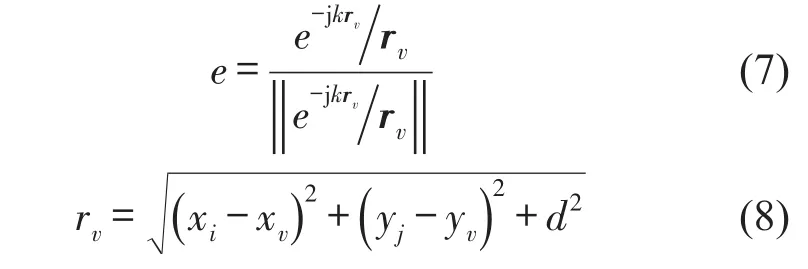
将传声器阵列测得的声压向量P与构造的虚拟声源向量e做内积运算用H表示向量的内积

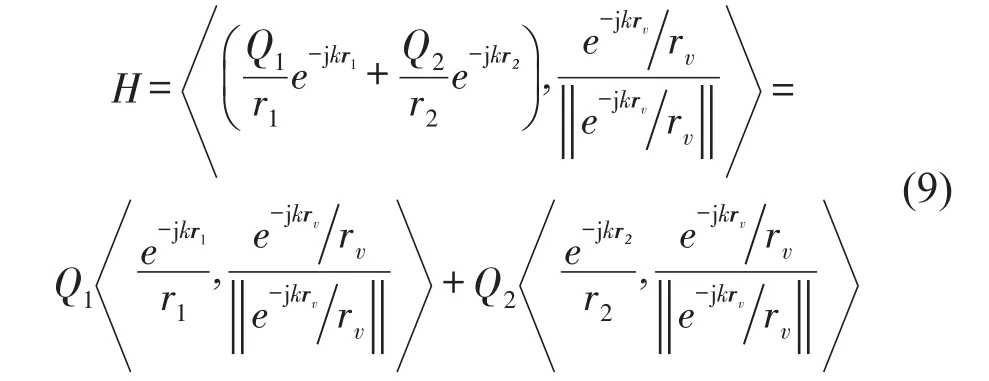
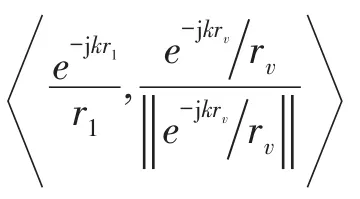
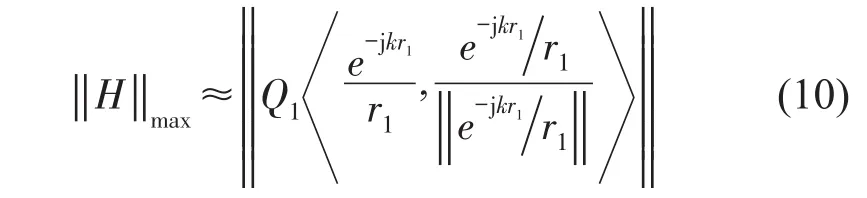
因此，当虚拟声源的位置与声源S1的位置重合时，声压向量与构造虚拟声源声压向量的内积模达到最大值||H||max。在Matlab中利用拟牛顿优化算法找到声源面上内积模的最大响应诊断第一个声源。将找到的声源位置坐标代入式（8）计算虚拟声源的距离向量rν。在向量内积模最大时，向量P与归一化的虚拟声源向量e线性相关，由下式计算出点声源S1的强度Q1

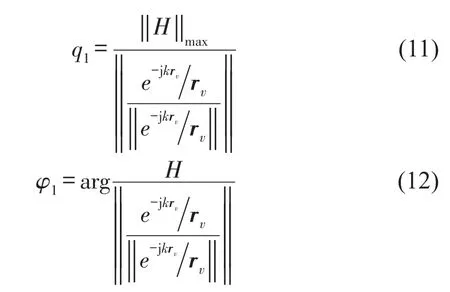
式（11）中||H||max表示声源位置处的内积模最大值，||.||表示向量的二范数，arg表示对复数取幅角；由此，声源S1的位置、强度和初相位均被识别出。

根据声源S1的位置、强度和初相位重构出其在阵列面上的声压分布，并按阵列顺序整合成声压向量P1，从总的声压向量P中减去P1，剩余的声压向量P2=P-P1；计算P2与构造的虚拟声源向量e的内积，在内积模最大响应的位置找出第二个声源，并由内积值计算S2的强度和初相位。从总的声压信号中减去声源S1和S2重构的位于阵列面上的声压信号；当阵列面上残余的声压信号很小，说明已识别出所有声源。

2　仿真算例

假设声源面上存在两个分别位于（-0.423 1，-0.465 7）m和（0.4728，0.450 6）m处的点声源S1和S2，声源辐射的频率均为1 000 Hz；S1和S2之间的间距为1.3 m；声源强度均为0.6（Pa·m），初相位分别为0.7 rad和1.2 rad；传声器阵列面为1.0 m×1.0 m，阵列面上传声器之间的间隔均为0.1 m，阵列面与声源的垂直距离为0.1 m；利用基于内积相关性的声源识别方法，在声源面上以估计的声源频率构造一个虚拟点声源，并将测得的实际声源声压向量与构造的虚拟声源辐射到阵列上的声压向量做内积运算，为了形象显示内积运算结果的变化趋势，对内积模取2为底数的指数运算处理，处理后的内积模变化趋势如图1所示，从图中可以看出有两个明显的峰值位置，代表两个声源的位置。声源信息的理论值与识别值的对比结果如表1所示。

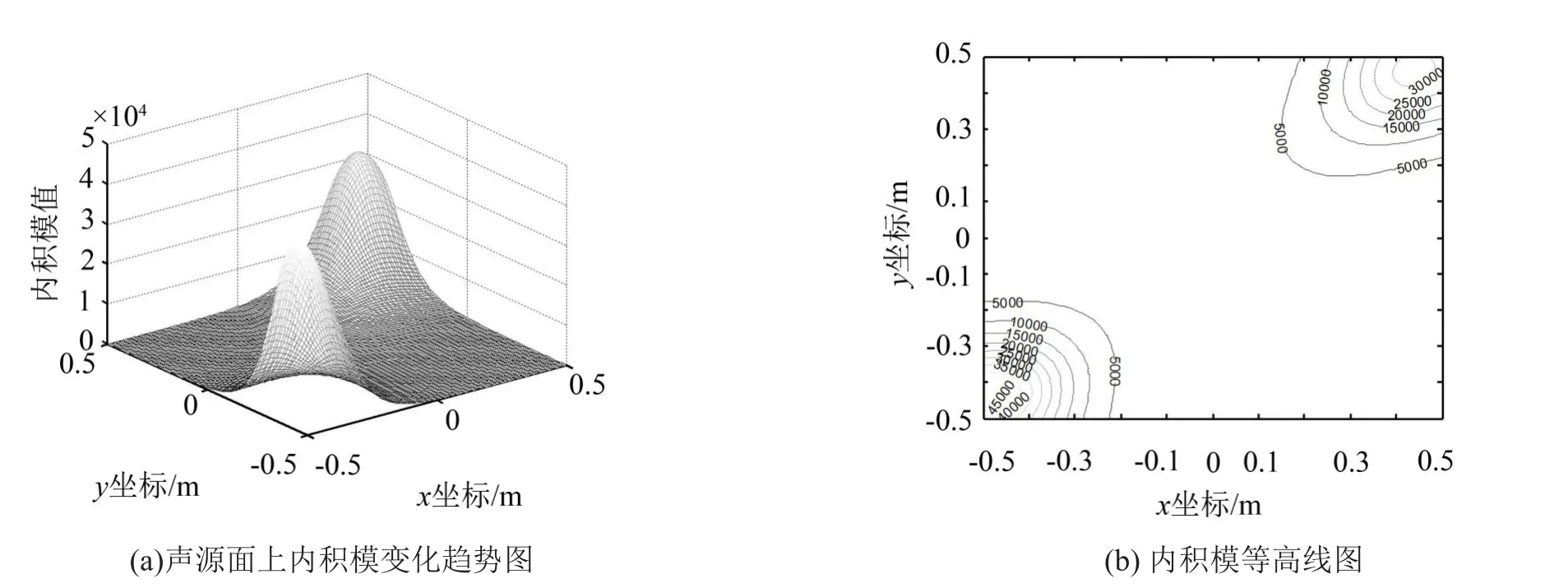
图1　内积模变化和等高线

表1　两个较远声源的识别结果

从表1的仿真结果可以看出，两个声源位置的识别结果与理论值相比都存在一定的偏差，识别出的声源强度与初相位也存在微小的误差，在工程运用中这种微小的识别误差不影响声源识别的效果，证明本文方法能用于识别两点声源；声源识别中产生的误差是因为声源彼此之间存在的相互干扰，在识别声源S1时，由于测得声压数据中有声源S2的贡献量。对于两个距离较远的声源来说，声源之间的干扰很小，这种误差可以忽略。

改变声源S1与声源S2之间的距离，使两个声源相距较近，令声源S1位于（-0.223 1，-0.265 7）m，声源S2位于（0.272 8，0.250 6）m，此时两个声源之间的距离为0.7 m，声源频率、强度、初相位及测量装置不变，计算声源面上的内积值变换趋势如图2所示。

从图2可以看出，当两个声源间的距离较近时，声源间的干扰严重，已无明显的两个峰值。利用拟牛顿优化算法在整个空间内搜索内积模最大响应的位置，声源的理论值与识别值的对比结果如表2所示。从表2可以看出，声源识别的结果产生了很大的误差，识别出的声源S1和S2的位置与真实位置偏差很大，声源强度和初相位的识别结果与理论值也有较大误差，说明声源间的干扰会影响识别精度，当声源间的距离很近时，干扰问题更为明显。

3　迭代循环相减原理

由于声压满足叠加原理，声压数据可以通过代数相减来降低声源之间的干扰。在利用内积相关性的基础上，引入迭代循环相减算法识别两点声源，以消除声源间相互干扰的影响，提高识别精度。其实现过程是计算声压向量与虚拟声压向量的内积模，通过内积模极值找到第一个位置点并求得第一个位置点的声源强度；从实测的声压向量中减去识别出的第一个声源信息再次计算与虚拟声压向量的内积模进而求得第二个位置点的声源信息。多次循环上述步骤直至阵列面上的残余声压很微弱，迭代循环过程结束。两点声源识别结合迭代循环相减的算法流程图如3所示。

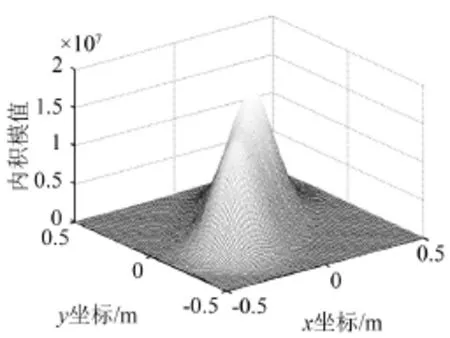
图2　声源面上内积模变化趋势图

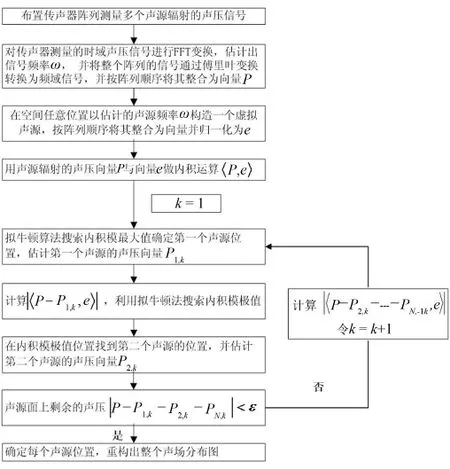
图3　迭代循环相减识别两点声源的流程图

表2　两个较近声源的识别结果

4　迭代循环相减仿真算例

对两个分别位于（-0.223 1，-0.265 7）m和（0.272 8，0.250 6）m位置处的点声源进行仿真研究，考察引入迭代相减算法后的声源识别效果。通过一次迭代循环相减，减去识别出的声源第二个声源，此时剩余的信号与虚拟声压向量做内积运算的内积值变化趋势如图4（a）所示；从总的声压信号中减去新的识别出的第一个声源的声压数据用来再次识别第二声源，此时声源面上内积模的变化趋势如图4（b）所示。从图4的内积模的变化趋势图中可以看出，一次迭代循环相减后内积模的峰值能明显区分出；五次迭代运算后声源面上剩余的声压峰值小于0.1 Pa时迭代终止，输出所有声源的识别结果。

迭代循环相减算法在运算过程中逐步减小声源间的相互干扰，传声器测量面上剩余的声压信号在迭代循环相减的过程中逐渐减小，剩余声压在迭代过程中的变化趋势如图5所示。

图5（b）中未迭代时测量面上剩余的声压的峰值为3.9 Pa，图5（c）中第一次迭代后剩余声压信号的峰值为1.1 Pa，图5（d）中经过五次迭代后剩余声压信号的峰值为0.1 Pa，此时阵列面上剩余的声压信号很微弱，由此判断声源信息均被识别出；声源信息的理论值、未迭代的识别值及经过五次迭代循环相减后的识别值的对比结果如表3所示。

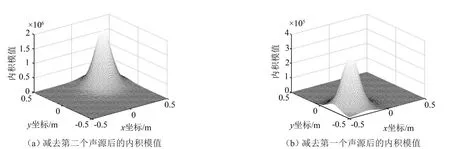
图4　声源面上内积模变化值

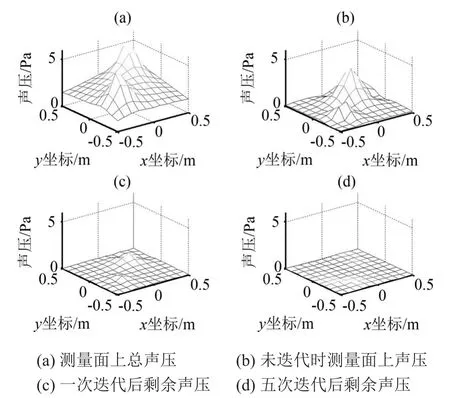
图5　剩余声压变化趋势

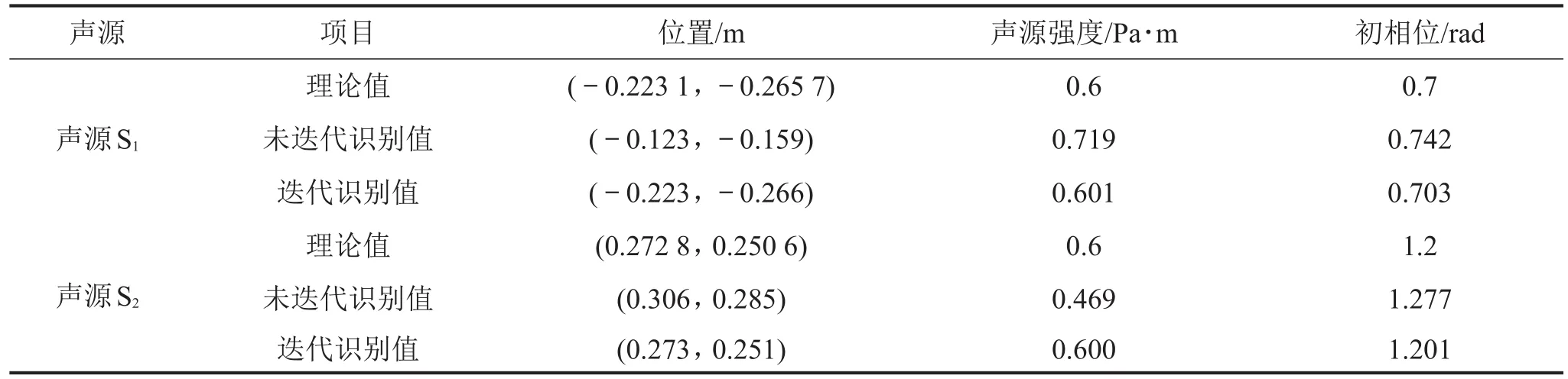
表3　结合迭代相减算法两点声源的识别结果

对比表3未迭代及采用迭代循环相减后的声源S1和S2识别值，发现通过本文方法结合循环迭代相减能准确识别声源的位置信息，声源强度和初相位的误差也在很小的范围内。

为了更形象地表述识别出的声源声压分布情况，根据声源的理论值和识别值分别重构声场信息。根据表3中的结果重构距声源面Δz=0.03 m位置的声压分布图，重构面上的理论声压和识别出的声压分布图如图6所示。

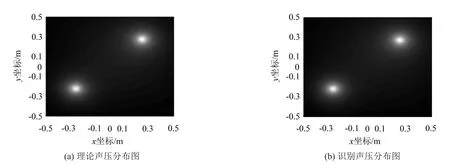
图6　重构面上理论声压和识别声压

5　结语

（1）本文提出利用内积相关性结合迭代相减算法识别两点声源，该方法不需要计算各个传声器相对于参考传声器接收到声压信号的时间差，而是计算实际测得的声压向量与虚拟声压向量的内积，通过搜索内积模的极值找到声源位置。

（2）对平面内不同距离的两点声源仿真结果表明，当两个点声源距离较远时，仅利用内积相关性原理的识别方法就可以较为准确地识别出两点声源；当两个点声源距离较近时，声源间的相互干涉影响识别精度，此时利用多次循环迭代相减能逐步减小其余声源对识别目标声源的干扰，找到的内积模极值的位置与实际声源更接近，因此能有效实现两点声源的识别。

［1］陈心昭.噪声源识别技术的进展［J］.合肥工业大学学报（自然科学版），2009，32（5）：609-614.

［2］WILLIAMS E G，MAYNARD J D.Holographic imaging without wavelength resolution limit［J］.Physical Review Letters，1980，45:554-557.

［3］CHRISTENSEN J J，HALD J.Beamforming［J］.B&&K Technical Review，2004（1）:1-31.485-510.

［4］胡伊贤，李舜酩.车辆噪声源识别方法综述［J］.噪声与振动控制，2012，32（5）：11-15.

［5］李青，毕传兴.基于Lab VIEW的近场声全息噪声源识别系统［J］.噪声与振动控制，2010，30（6）：140-144.

［6］刘译蔚，杨建华.由波束形成的噪声源识别方法对比研究［J］.噪声与振动控制，2015，35（1）：165-168.

［7］杨洋，倪计民.基于波束形成的发动机噪声源识别及声功率计算［J］.内燃机工程，2013，34（3）：39-43.

［8］冒凯炫.基于柯西-施瓦茨不等式的声源识别方法研究［D］.镇江：江苏大学.

Application of Inner Product Correlation with Iteration Circular Subtraction to the Identification of Bi-pointAcoustic Sources

KOU Hai-liang，MAO Kai-xuan，ZHAO Xiao-dan
（College ofAutomobile and Traffic Engineering，Jiangsu University，Zhenjiang 212013，Jiangsu China）

A new bi-point acoustic source identification method based on inner product correlation is presented.This method can construct the virtual sources in a sound source plane.Through calculating the sound pressures of the virtual sources in a microphone array，the sound pressure vector can be constructed by combining these pressure values into a vector.Then，this vector is normalized and used to perform an inner product operation with the measured signals. Optimization algorithm is used to search for the maximum inner product modulus.When the inner product modulus reaches the maximum，the source location can be identified according to the inner product correlation principle.When the two sources are close to each other，the identification precise is greatly affected by their mutual interference.Then，the iteration circular subtraction is introduced to reduce the interference.The iteration process does not terminate until the remnant sound pressure value vanishes.Simulation results show that the acoustic source identification method based on the inner product correlation combined with iteration circular subtraction can identify the two sound sources accurately.

acoustics；acoustic source identification；inner product；iteration circular subtraction；microphone array

O422.6

ADOI编码：10.3969/j.issn.1006-1335.2016.05.004

1006-1355（2016）05-0015-04

2016-03-16

江苏高校优势学科建设工程资助项目（苏政办发［011］6号）；江苏大学高级专业人才科研基金项目（11JDG096）

寇海亮（1983-），男，河南省洛阳市人，硕士研究生，研究方向为噪声与振动控制。E-mail:badun1022@163.com

赵晓丹（1963-），男，江苏省镇江市人，教授，博导，研究方向为噪声与振动控制、信号处理。E-mail:zhaoxiaodan@ujs.edu.cn