高速列车作用下箱梁桥箱内振动噪声分布研究
程海根,蒋伟超
(华东交通大学土木建筑学院,南昌 330013)
高速列车作用下箱梁桥箱内振动噪声分布研究
程海根,蒋伟超
(华东交通大学土木建筑学院,南昌 330013)
为解决高速铁路线上箱梁桥日常检查与列车运营之间的冲突,探讨列车正常运行时箱梁内部噪声对日常检查工作造成的影响,桥梁结构振动辐射低频噪声会对检测人员造成极大危害,研究箱梁内部噪声分布有着重要的现实意义。结合车桥耦合振动和声传播理论,通过建立桥梁振动辐射有限元-边界元的求解体系,以78 m变截面混凝土箱梁桥作为实体模型,得出箱内瞬态噪声声场特性。分析结果表明,在车桥耦合振动所产生的箱内声辐射噪声分析中,变截面处声压值增大,且列车交汇产生的声压值大于单向行车产生的声压值。当箱内添加吸声材料后,可降低噪声水平,保障检测人员身体健康。
桥梁振动; 低频噪声; 瞬态边界元;声压分布
高速铁路快速发展带来方便与快捷的同时,保证线路安全是最为关键的问题。高速铁路线路在日常检查中,均禁止工务人员利用运营期间天窗点上线作业,对线路结构物及相关设备的检查均要求安排在列车停运期间,该时段大多处于晚11时至次日凌晨6点,增加了工务人员的劳动强度。高速铁路线上的桥梁以标准跨径箱梁或变截面箱梁为主,工务检查人员在高铁运行过程中可以对桥梁结构内部做必要的检查而不会影响列车正常运营,但在线路运营时进行箱梁内部检查面临的最大问题就是桥梁振动辐射噪声[1]。桥梁箱内是结构自身振动产生的低频噪声主要的辐射区域,低频噪声对于检测人员的身体状况造成一定影响,包括神经衰弱、失眠、头痛、记忆力衰减、综合判断力下降等多种神经官能症。通过分析箱内噪声声压分布,来指导采用合理的降噪方式和保护措施,有效地保障检测人员工作状态中的身体健康。
K.W.Ngi, C.F.Ng[2]通过FFT算法对混凝土简支箱梁结构进行噪声辐射计算,得出的结果与简支箱梁实测噪声进行对比。结果表明,列车行驶速度为140 km/h通过混凝土简支梁桥时,箱梁的振动频率集中在20~157 Hz。其中,频率的峰值出现在43 Hz和53 Hz。Theeraphong, Chanpheng[3]结合了桥梁低频振动的研究结论,提出声辐射模型在研究降低结构声辐射的问题上比从振动模型上控制结构声辐射效果更好。同时指出,利用声辐射模态可以更好地描述结构的声辐射特性,并将结构表明的振动速度和声辐射功率相互结合进行振动声辐射研究。N.Ouelaa, A.Rezaiguia, B.Laulagnet等[4],在车辆-轨道-桥梁耦合振动模型中,使用模态叠加法,并考虑车辆整体质量和阻尼,利用Newmark迭代方法对耦合方程进行求解。根据求解结果推导出因结构振动引发的声辐射波动方程。对Helmoltz方程求解,得到任意点的声压分布。李小珍,吴国强[5],使用边界元法和车-桥耦合理论对高速列车作用下箱梁的噪声辐射情况进行研究,通过模拟改变桥梁墩台高度、地面反射、声屏障以及不同车速等参数进而对箱梁噪声辐射进行比对分析。张鹤,谢旭[6],利用格子梁理论,通过建立车桥耦合模型进行有限元数值计算,得到交通荷载作用下的动力相应特性。并采用边界元法对桥梁声辐射特性进行分析,考虑地面反射对声场分布的影响,最终得到桥梁在空间声场中的分布规律。
对于声辐射问题可以通过一定边界条件下波动方程的定解来描述,按照分析方法的不同可以分为时域分析和频域分析[7-8]。利用时域分析法计算瞬态声辐射规律,以78 m变截面混凝土简支箱梁桥为研究对象,在ANSYS有限元软件中进行车桥耦合振动得到桥梁结构振动响应结果,并将响应结构导入声学软件LMS Virtual.Lab中进行声场计算,通过对比得到在混凝土箱梁内部的声压分布情况,为控制车桥振动产生的噪声提供可行性方案。
1 瞬态声波传播理论及边界元算法
在声场当中,小振幅声波的声压p的三维波动方程为在空气中以声压p为变量的声波控制方程
(1)

假设波动方程的基本解为S1=[p*,q*],该解存在于空间域Ω、时间域T之中,也必须满足声波控制方程。在声场的控制方程中,可以通过声压和速度来对瞬态声场进行描述
(2)
将q=∂p/∂n定义为声通量。可由声通量来对声压在传播边界条件
(3)
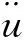
在时间域内进行声辐射瞬态声压求解需要对初始条件进行重新定义,将S1和S2的初始声压定义为p,并将声压关于时间的一阶倒数v定义为
(4)
(5)
对公式(4)、(5)进行拉普拉斯变换,得到声波时域计算边界积分方程
(6)
边界积分方程经过时域离散后,可以进一步通过空间的离散将积分方程转化为代数方程,该问题的边界离散通过在积分边界划分边界单元实现。
(7)
对于求解域Ω内的任意点可以由边界Γ上的声压和声通量求得。声辐射计算中,可以通过结构表面振动加速度得到结构边界上各节点的声通量,可以表示为
(8)
其中,p(αg)、q(∂g)为节点声压和声通量的向量;pn为第n时间步下各节点声压形成的声压向量。最终通过式(8)计算节点声场声压
(9)
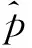
2 混凝土箱梁声辐射计算模型
混凝土箱梁计算模型采用78 m变截面简支箱梁,梁截面采用单箱单室斜腹板结构。梁体采用C50混凝土,弹性模量34.5 GPa,材料密度2 600 kg/m3,泊松比0.3。LMS Virtual.lab进行瞬态边界元分析过程中边界元网格必须是三角网格,故使用自由网格划分。加载采用节点加载(图1),根据计算的要求,列车开行的方式为单向行车、双向行车、右股先上1/4跨左股再上桥、右股先上1/4跨左股再上桥。数组定义为单向4节车厢,每节车长25 m,轮轴距20 m。选择箱内声辐射场点如图2所示。
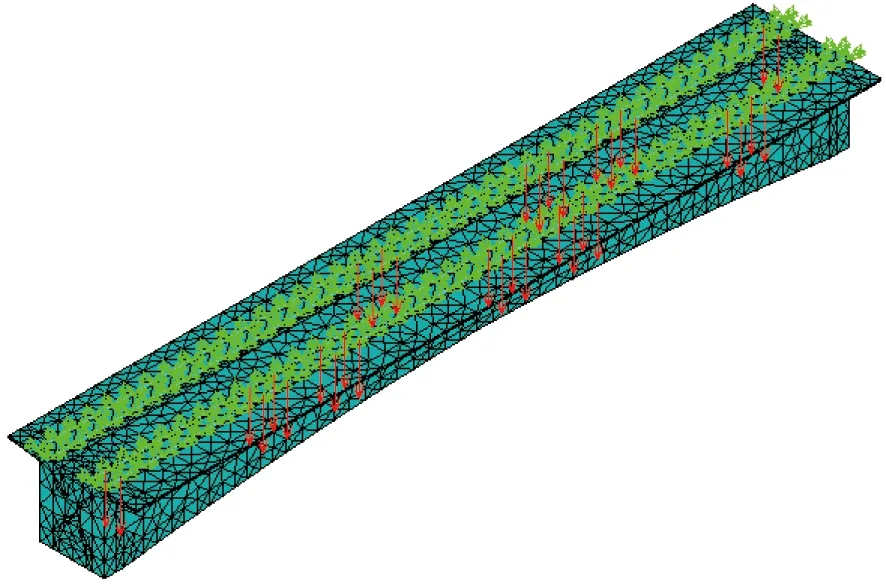
图1 轮轨力加载方式
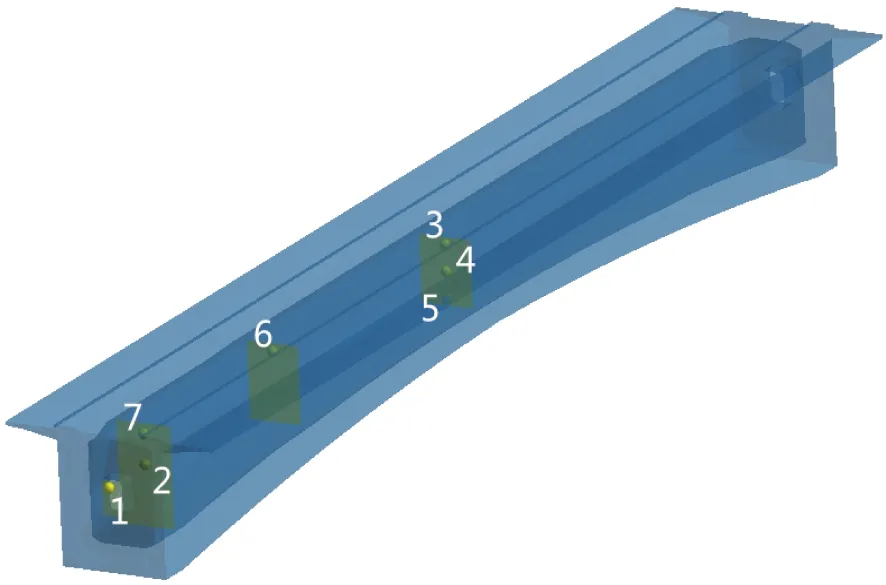
图2 场点选择
图2中,场点1为端口距底板1.7 m处,场点2为距两端4 m处、距底板1.7 m处。场点3、4、5分布为跨中截面为距顶板20 cm处(检测顶板时双耳的位置)、距底板1.7 m处(人站立时双耳的高度)、距底板1 m处(人蹲下时双耳的高度);场点6、7为1/4截面、1/2截面距顶板20 cm处场点。
3 声辐射数值分析
3.1 变截面对声压的影响
选择图2中场点1、2,通过对比分析变截面处声压分布的影响。
从图3中看出,变截面处声压变化明显,相距4 m、等高度的场点声压相差10.54 dB。噪声辐射过程中,遇到混凝土截面会出现发射现象,造成变截面处声压增强,且通过箱梁入口向外辐射的声压较小。
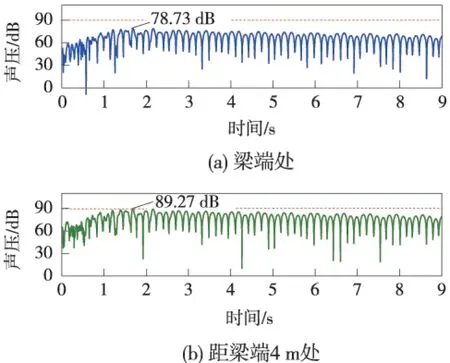
图3 场点1、2声压分布
3.2 箱内竖向截面处声压分布情况
选取在速度为200 km/h时,通过4种行车方式下声压分布,得出箱内跨中(图2中场点3、4、5)竖向截面声压分布情况,如图4~图6所示。
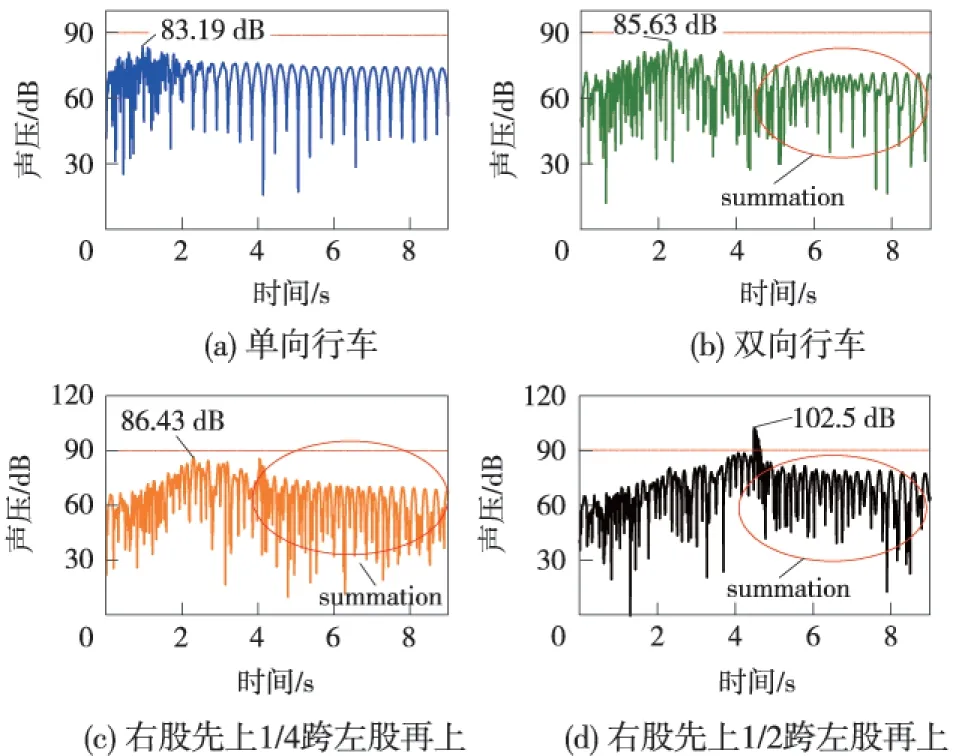
图4 4种行车方式下场点3声压分布

图5 4种行车方式下场点4声压分布
由图4~图6可知,按场点位置不同,声压值从大到小依次为:距梁顶板20 cm处声压值>距梁底板1 m
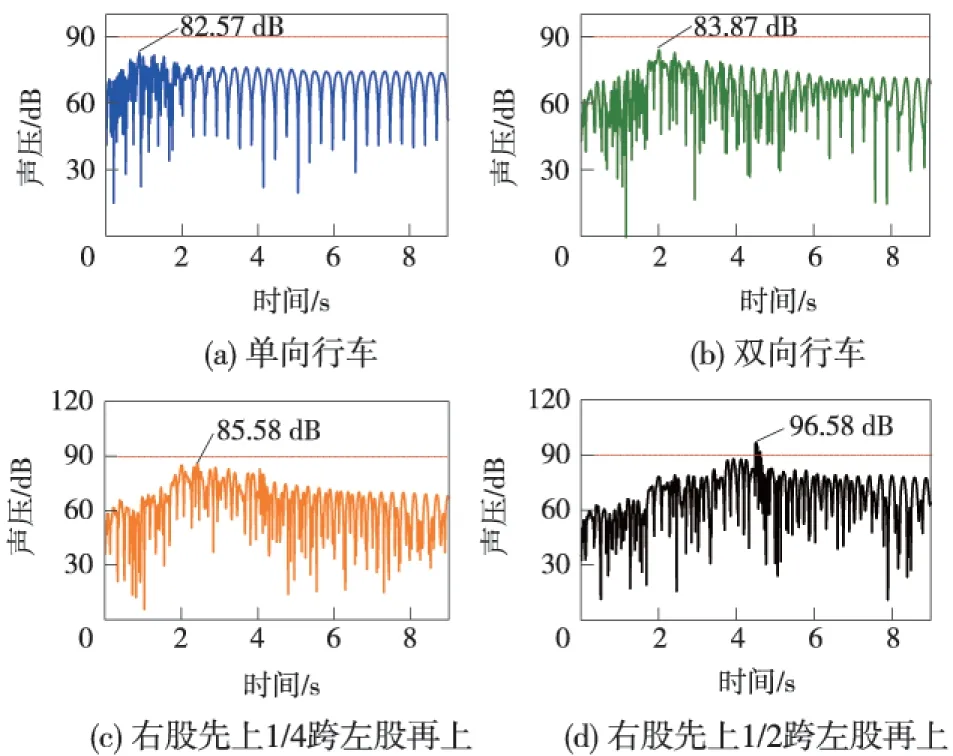
图6 4种行车方式下场点5声压分布
处声压值>距梁底板1.7 m处声压值。按行车方式不同,声压值从大到小依次为:右股先上1/2跨左股再上声压值>右股先上1/4跨左股再上声压值>双向行车
声压值>单向行车声压值。在图4中,除单向行车以外,3种行车方式下声压值变化趋势发生了一定的改变,在声压分布中两列波形出现叠加现象,但是不同的加载方式导致波形的极值点有所不同。在降噪中,可以考虑将声波的波峰波谷相叠加的方式降低噪声值。
在表1中,不同行车方式下出现声压峰值的时间不同。根据计算,单向行车中,4节车厢中的2节车厢满布桥面,则出现声压最大值;双向行车中,双向4节车厢(共8节车厢)满布桥面,则出现声压最大值;在左股先上1/4跨左股再上行车方式中,左右两股共4节车厢满布桥面时,声压出现最大值;在左股先上1/2跨左股再上行车方式中,右侧所有车厢全部行驶离开桥面、左侧只有最后一节车厢留在桥上其余三节车厢行驶离开桥面,声压值出现最大。同时,在左股先上1/2跨左股再上行车方式中,声压值最高,由此看出,在变截面箱梁箱内,噪声会出现叠加的情况,而且噪声值的大小很难在列车驶离后出现下降。

表1 车速200 km/h时不同加载方式下声压最大值
3.3 78 m变截面箱内横向截面处声压分布情况
选择竖向截面场点声压最大的顶板附近场点,选取车速200 km/h时,双向加载下箱内距梁端4 m处场点、1/4截面处场点、跨中截面处场点(图2中场点3、6、7)声压。
在同一横截面不同位置声压值由大到小依次为:1/4跨截面声压>距梁端4m处截面声压>跨中截面声压,如图7所示。

图7 200 km/h时双向行车声压情况
4 优化方案
为保护桥梁检测人员的身体健康,从降噪的角度出发,考虑优化桥梁结构特性的方式来起到降低噪声的作用。在混凝土箱内的上顶板,安装吸声材料,通过对比跨中截面顶板附近(图2中场点3、4、5)的场点。选用78 m箱梁双向加载,分别在无吸声材料、吸声材料声阻抗400 kg/m2·s、吸声材料声阻抗600 kg/m2·s三种情况下进行对比,如图8所示。

图8 不同吸声材料下跨中点声压分布
由图8可以看出,在箱梁箱内顶板处安装声阻抗为400、600 kg/m2s的吸声材料,噪声值出现了明显的降低。可将原有箱内最大声压值降低10 dB以上。同时可以发现,在添加吸声材料之后,声压值出现了快速衰减的情况。3种情况中,声压最大值出现在左右两股上,前两节车厢驶离桥面,第三、四节(共四节)车厢满布桥面。在3.6 s时,箱内出现声压极值,此时左右两股车辆同时驶离桥面,箱内声压出现叠加增强的情况。车辆驶离桥面后,噪声被吸声材料吸收,会在很短的时间内出现大幅度的衰减,迅速将噪声值降至人体可承受的范围之内。由此可以看出添加吸声材料具有一定的降噪保护的作用。
对比添加声阻抗率为400、600 kg/m2·s的吸声材料,随着声阻抗率提高,箱内声压值并没有较大的变化。使用声阻抗率为600 kg/m2·s的材料将声压值降为零的时间比使用声阻抗率为400 kg/m2·s的材料将声压值降为零的时间更快。可以总结出,使用不同声阻抗率的吸声材料在降低声压值方面产生的效果相同,但是出现效果的时间不同。
5 结论
根据对78 m变截面混凝土箱梁在车桥耦合的作用下得到振动响应,并根据响应结果进行瞬态边界元声学计算,得到在不同的工况下混凝土箱梁箱内的噪声分布情况,主要结论如下。
(1)噪声辐射过程中,混凝土截面形式改变,使得噪声出现发射现象,造成变截面处声压增强,且噪声通过箱梁入口向外辐射的声压较小。
(2)箱内噪声分布按场点位置不同,竖向声压值从大到小依次为:距梁顶板20 cm处声压值>距梁底板1 m处声压值>距梁底板1.7 m处声压值。横向截面声压值由大到小依次为:1/4跨截面声压>距梁端4 m处截面声压>跨中截面声压。按行车方式不同,声压值从大到小依次为:右股先上1/2跨左股再上声压值>右股先上1/4跨左股再上声压值>双向行车声压值>单向行车声压值。
(3)列车双向交汇时声压值变化趋势不同于单向开行产生的声压情况,在声压分布中两列波形出现叠加现象,但是不同的加载方式导致波形的极值点有所不同。在降噪中,可以考虑将声波的波峰波谷相叠加的方式降低噪声值。
(4)添加吸声材料可以有效地将产生的噪声迅速控制在人体可承受范围内。使用不同声阻抗率的吸声材料在降低声压值方面产生的效果相同,但是出现效果的时间不同。
[1]焦大化.铁路环境噪声控制[M].北京:中国铁道出版社,1990.
[2]K.W.Ngai and C.F.Ng. Structure-noise and vibration of concrete box structure and rail viaduct[J]. Journal of Sound and Vibration, 2002,255(2):281-297.
[3]Theeraphong ChanPheng, Hitoshi Yamada, Toshio Miyata, Hiroshi Katsuchi. A pplication of radiation modes to the problem of low frequency noise from a highway bridge[J]. Applied Acoustics, 2004,65:109-123.
[4]N. Ouelaa, A. Rezaiguia, B. Laulagnet. Vibro-acoustic modeling of a railway bridge crossed by a train[J]. Applied Acoustics, 2006,67:461-475.
[5]李小珍,张讯,李亚东.高速铁路简支箱梁结构噪声的边界元方法[J].土木工程学报,2011,44:95-101.
[6]张鹤,谢旭.交通荷载作用下桥梁振动与噪声问题研究[D].杭州:浙江大学,2010.
[7]余爱萍,张重超,骆振黄.瞬态声场特性的时域边界元分析和实验研究[J].上海交通大学学报,1989,23(3):82-89.
[8]蒋伟,何正耀,王东海.辐射体声场计算的综合Helmholtz积分公式法[J].电声基础,2006,10:9-12.
[9]谢旭,张鹤,山下幹夫,等.桥梁振动辐射低频噪声评估方法研究[J].土木工程学报,2008,41(10):53-59.
[10]Nefske D J,Wolf J A, Jr, Howell L J. Structural-acoustic finite element analysis of the automobile passenger compartment: a review of current practice. Journal of Sound and Vibration, 1982,80(2):247-266.
[11]胡新伟,黄醒养.高架轨道梁振动与结构噪声的数值模拟[J].低温建筑技术,2007(2):54-56.
[12]丁桂保,郑史雄.高速铁路桥梁的低频噪声研究[J].西南交通大学学报,1998,33(2):127-131.
Research on Distribution of Internal Vibration Noise of Box Girder Bridge under High-speed Train
CHENG Hai-gen, JIANG Wei-chao
(School of Civil Engineering, East China Jiaotong University, Nanchang 330013, China)
In order to solve the contradiction between the daily inspection of high-speed railway box girder bridge and train operation, this paper focuses on the impact of the internal noise on the daily inspection activities due to the bridge structure with low-frequency vibration radiation noise, which may cause great harm to the inspection people. Proper control of bridge internal noise distribution proves important practical significance. The transient noise induced by vehicle-bridge coupling vibration is investigated with a solving system based on FEM and BEM. A 78 m non-prismatic concrete box girder bridge is taken as the entity model to identify the transient noise characteristics of box girder bridge. The radiation noise analysis shows that sound pressure at non-prismatic section increases, meanwhile, the sound pressure produced where two trains are meeting is greater than that produced by train running in one direction. Adding sound-absorbing material can reduce noise level for the good of inspection people.
Bridge vibration; Low-frequency noise; Acoustic transient boundary element; Sound pressure distribution
2014-11-19;
2015-03-16
程海根(1971—),男,副教授,2004年毕业于西南交通大学桥梁与隧道工程专业,工学博士。
1004-2954(2015)09-0093-05
U238; U44
A
10.13238/j.issn.1004-2954.2015.09.021

