复杂声场环境下目标声源声场重建误差分析
张诗科,朱海潮,谢志敏,毛荣富
(1.海军工程大学 振动与噪声研究所,武汉 430033;2.船舶振动噪声重点实验室,武汉 430033;3.解放军海洋环境专项办公室,北京 100081)
复杂声场环境下目标声源声场重建误差分析
张诗科1,2,朱海潮1,2,谢志敏3,毛荣富1,2
(1.海军工程大学 振动与噪声研究所,武汉 430033;2.船舶振动噪声重点实验室,武汉 430033;3.解放军海洋环境专项办公室,北京 100081)
针对目标声源在复杂声场环境下进行声场重建易受到其它声源干扰的问题,提出存在干扰源声场、散射声场及目标声源声场的混合声场环境下基于单面声场分离技术的目标声源声场分离及重建方法。首先,通过理论分析和公式推导,清除干扰源声场及散射声场的影响;然后,利用传递函数性质对声场分离及重建误差进行分析,并对计算公式中存在的奇异性问题予以消除,得到高分辨率的声场重建图像。数值仿真表明:利用常规的单面声场分离技术很难重建混合声场环境下目标声源的声场,而利用本文研究的声场分离及重建方法能够很好反映目标声源声场的实际情况,提高声场重建的精度。
声学;声全息;复杂声场;声场重建;误差分析
近场声全息(near-fieldacousticholography,NAH)技术研究日趋成熟,在噪声源识别定位、声场预测和可视化方面得到广泛关注。但是,近场声全息技术对试验条件要求较高,声源必须位于测量面同侧,测量面另一侧为自由场,而实际的测量环境比较复杂,很难满足一侧为自由场,要想实现目标声源的声场重建,就需要在非自由声场环境下对近场声全息技术进行研究。在不需要预知声源位置信息的情况下,通常采用声场分离技术作为非自由场环境下去除全息面背侧干扰源影响的前处理技术。
目前在非自由声场环境下声场分离技术的应用研究中形成了基于空间声场变换理论、边界元法、波叠加法、统计最优法等多种算法声场分离技术。在测量面的选取上又有单面声场分离技术和双面声场分离技术之分。于飞、陈剑等针对平面和柱面测量面,利用波数域内的声场外推理论及声压的标量叠加理论,构造了双全息面的声场分离公式[1-2];利用波数域内的欧拉公式及粒子振速的矢量叠加理论,构造了单全息面的声场分离公式,克服了近场声全息和基于声强测量的宽带声全息的应用局限[3]。Wu等利用球面波在径向上体现梯度变化的信息,提出了混合近场声全息技术[4],但在球面波最优截止阶数选取上仍需要增加一个辅助面,实际测量中需要两个测量面。毕传兴等提出基于质点振速的双面声场分离技术,在近场声全息声场重建中取得很好的效果[5]。毕传兴、张永斌等基于欧拉方程及有限差分近似,推导了单面声场分离技术的近场声全息理论公式[6],并用实验检验了在有干扰源的情况下实现声场分离及重建的有效性,同时又将声场分离技术和Patch NAH进行了结合,对非自由声场环境下局部近场声全息进行了研究[7]。
在强干扰源的声场环境下,干扰声源在目标声源表面产生的散射效应明显,实际的测量环境变得更为复杂,此时的声场环境应包含目标声源的声场、干扰源产生的声场及散射声场。以上基于不同算法或不同测量面的声场分离技术的研究是在目标声源声场及干扰源声场环境下进行的,剔除干扰源声场的影响能够提高目标声源声场的重建精度。但是,目标声源的声场分离及重建时只考虑干扰源声场而忽视散射声场的影响,会给目标声源声场的分离及重建带来很大的误差,尤其在散射声场影响较为明显时,会导致目标源声场分离及重建的失败。所以,在实际复杂的声场环境下实现目标源声场的重建,不得不同时剔除干扰源声场及散射声场的影响。本文对复杂声场环境下基于单面声场分离技术的平面NAH理论进行了深入研究,推导存在干扰源声场、散射声场及目标源声场的混合声场环境下目标源声场分离及重建公式,同时剔除了干扰源声场及散射声场的影响,从传递函数性质对复杂声场环境下目标声源声场分离及重建误差进行分析,对推导公式中存在的奇异性问题进行分析并用1/kz因子平均值法及K空间积分法予以消除,同时采用滤波器对噪声信号进行处理,有效提高了重建精度,最后通过数值仿真对研究理论进行了验证。
1 理论研究
在平面z=zS的Dirichlet边界条件和Neumann边界条件下,波数域内声源面的声场重建公式[8]
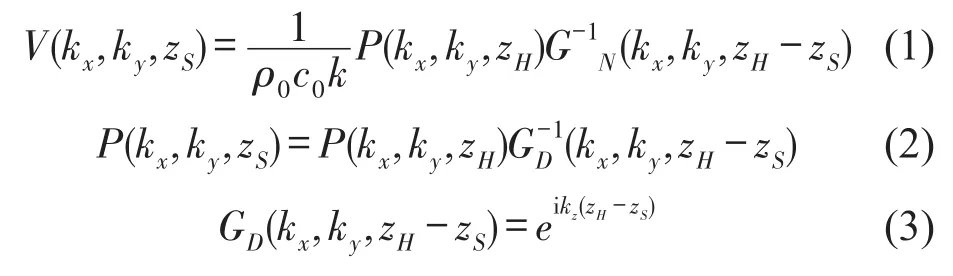
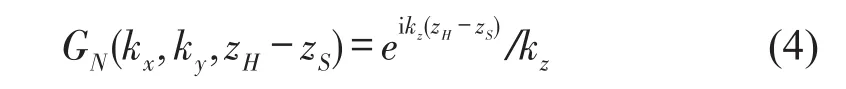
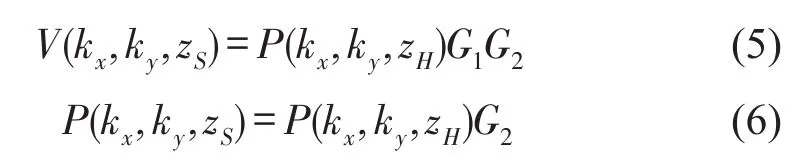
当zH-zS=0时,即在同一平面上法向质点振速与声压的关系如下
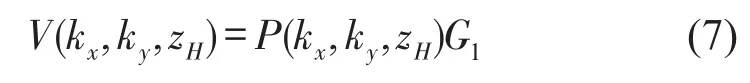
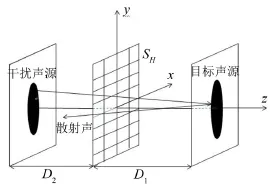
图1 单全息面与声源的空间位置关系图
如图1所示,在复杂声场环境下,全息面上测量得到的声压和质点振速由目标声源产生的声场、干扰源产生的声场以及干扰源在目标声源表面产生的散射声场三部分组成。以全息面中心为坐标原点建立空间直角坐标系,可以得到
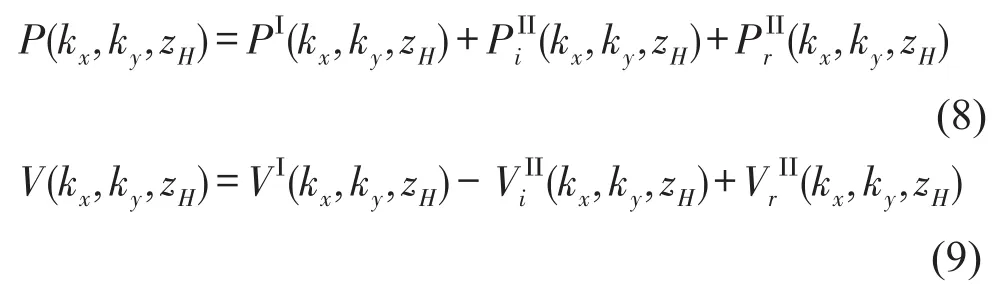
当散射效应显著时,要实现目标声源的声场重建必须考虑散射声场的影响,彻底剔除干扰声源的影响[9]。测量面上的散射声可通过反射系数作为边界条件求出[10],从而可得到与)的关系,即
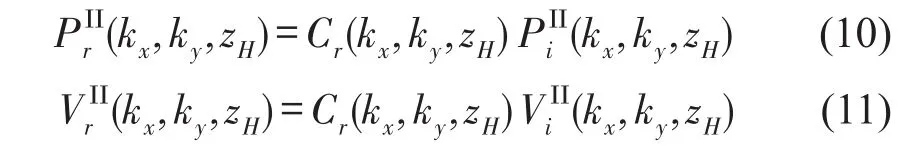
式中Cr(kx,ky,zH)是目标声源表面材料的复平面波反射系数[11]。
将式(10)、式(11)代入式(8)、式(9)可得
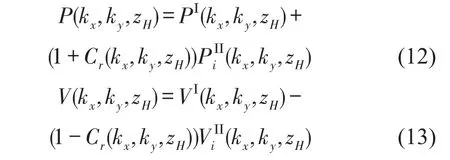
由式(7)声压和质点振速之间的关系可得
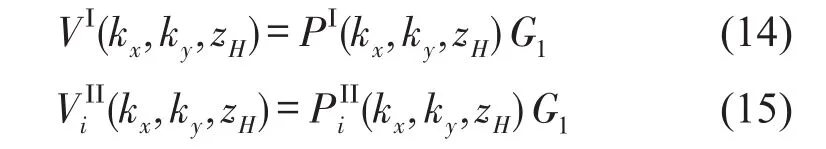
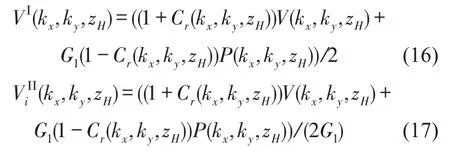
由上式即可得到目标声源在全息面上的声压和法向质点振速,分别将式(16)、式(17)代入式(5)、式(6)可重建声源面上声压和质点振速,即
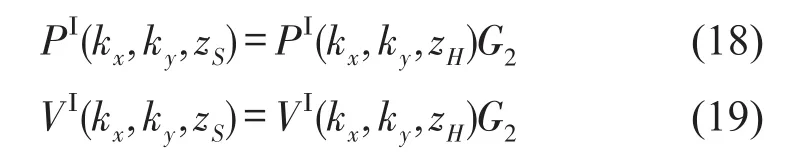
式(18)、式(19)用全息面上的法向振速重建声源面上的法向振速,全息面上的声压重建声源面上的声压。
由式(7)对式(18)、式(19)进行变换可得
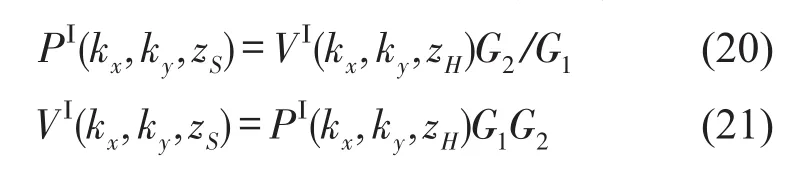
式(20)、式(21)用全息面上的法向振速重建声源面上的声压,全息面上的声压重建声源面上的振速。
对式(18)、式(19)、式(20)、式(21)进行Fourier反变换即可得到重建面上的目标声源的声压和质点振速。
2 数值仿真与误差分析
2.1传递函数性质的影响分析
图2是不同频率Kx(Ky=0)下传递函数G1G2的幅值,随着频率增大辐射圆半径逐渐增大,辐射圆内变化比较平缓,辐射圆外随|kx|增大G1G2值逐渐增大且频率越小增加越快。若用声压重建法向振速,信噪比如果过小,则在高波数区域倐逝波及噪声成分会被G1G2放大,从而导致目标声源声场重建失败,且频率越小放大倍数越大,重建精度越低,所以需要对声压进行消噪处理,从而提高目标声源的声场的重建精度。
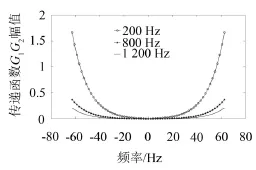
图2 不同频率下传递函数G1G2幅值
图3是不同频Kx(Ky=0)下传递函数的幅值,传递函数在辐射圆上具有奇异性,且频率越高,奇异性越明显,可通过求1/Kz因子的平均值方法来消除奇异性的影响[12],如图4所示。
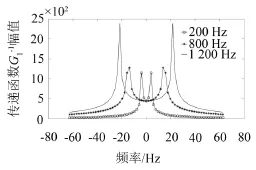
图3 不同频率下传递函数幅值
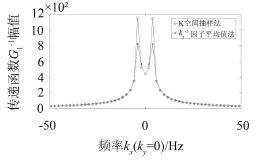
图4 基于K空间抽样法与平均值法的幅值
辐射圆上的奇异性得到有效消除。由图5可以看出,K空间积分法相比于K空间抽样法能够消除声场重建过程中辐射圆上的奇异性,但是在高波数区域幅值快速增大,辐射噪声成分也会被放大,若用式(20)进行声场重建,会造成很大的重建误差。因此需要在高波数域进行滤波处理,避免将噪声误差放大。对于信号的消噪可采用文献[13]中提到的滤波器及运用能量法估算信噪比进而选取截止波数的方法予以处理。
2.2不同声源的数值仿真
仿真中选取受激励的简支钢板作为目标声源,脉动球作为干扰声源。简支平板参数如下:平板尺寸为0.8 m×0.8 m,厚度为0.008 m,杨氏模量E为2× 1011Pa,泊松比υ取0.28,密度 ρ为7 800 kg/m3。刚性脉动球半径为0.01 m,振动速度为0.08 m/s。取钢板左下角为坐标原点,在点(0.125、0.125)处采用单频激励,激励力频率为600 Hz。脉动小球位于点(0.1、0.1、0.5)处,激励频率与板保持一致。仿真中假设钢板表面是刚性边界,则脉动球在钢板表面产生的散射声场相当于在(0.1、0.1、-0.5)处相同的脉动小球产生的声场。
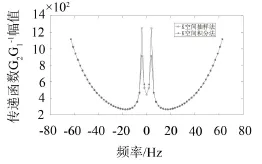
图5 K空间抽样法与积分法的?幅值
测量面位于zH=0.05 m的平面上,采样间隔在x和y方向上均为s=0.05 m,采样点数32×32且重建时对声压及质点振速数据补零,以消除FFT算法的使用而产生的卷绕误差和小测量孔径带来的吉布斯效应,重建面位于zS=0.02 m的平面上,测量面上声压和质点振速由钢板和脉动小球共同产生。为使仿真情况更接近实际测量环境的情况,对测量面的声压数据加入信噪比为50的随机白噪声。
声压和质点振速重建误差分别为
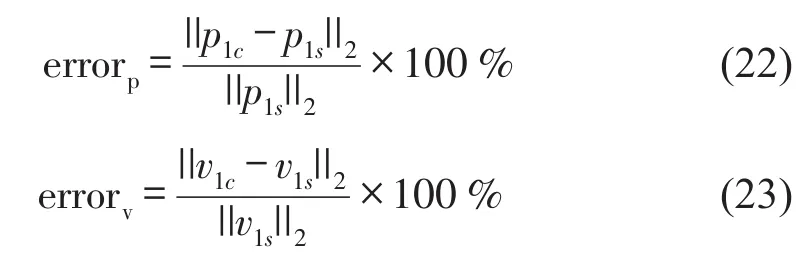
式中p1c、v1c分别表示重建的声压和质点振速,p1s、v1s分别表示对应的理论值。
图6至图11给出了600 Hz时,复杂声场环境下利用基于声压—质点振速测量的声场分离技术的平面NAH理论重建钢板的辐射声压及质点振速与理论值比较的图像。
其中,图6和图9表示忽略散射时重建源面的声压幅值及质点振速幅值,图7和图10表示重建源面的理论声压幅值及质点振速幅值,图8和图11表示剔除散射时重建源面的声压幅值及质点振速幅值。从图中可以看出剔除散射重建声场比忽略散射重建声场更能反映目标源声场的真实情况。
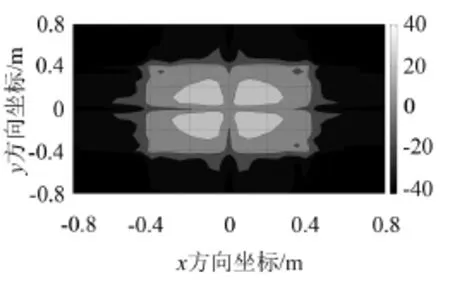
图6 忽略散射重建源面声压幅值
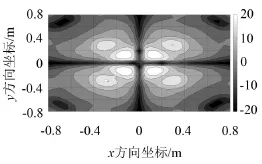
图7 重建源面理论声压幅值

图8 剔除散射重建源面声压幅值
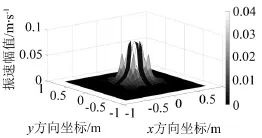
图9 忽略散射重建源面振速幅值
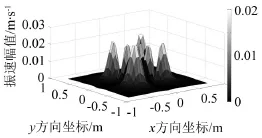
图10 重建源面理论振速幅值
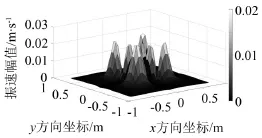
图11 剔除散射重建源面振速幅值
忽略散射时,由式(19)基于质点振速—质点振速的重建误差为91.52%;剔除散射时,由式(19)基于质点振速—质点振速的重建误差为8.13%。忽略散射时,由式(18)基于声压—声压的重建误差为105.23%;剔除散射时,由式(18)基于声压—声压的重建误差为25.74%。剔除散射时基于声压—声压的重建误差之所以较大是由于当平板为刚性面时,由式(17)可得
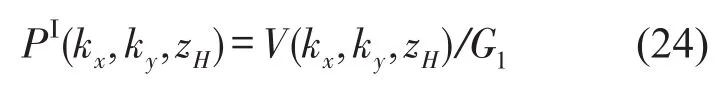
由声场中某位置的声阻抗率的定义可知

对平面波的情况,平面声波的声阻抗率为

因此,在平面声场中,各位置的声阻抗特性是一个固定的实数,只有被研究声源的声阻抗特性Zs≈ρ0c0时,才能保证声场重建的精度[12]。G1图像可知,G1是变化的值,并不是一个固定的实数值,所以在声压重建振速或振速重建声压的声场重建过程中,由G1的性质分析可知PΙ(kx,ky,zH)存在较大的分离误差,故对声压进一步重建时依然会存在较大的误差。由此可得,基于声压—声压的重建误差小于基于质点振速—声压的重建误差,基于质点振速—质点振速的重建误差小于基于声压—质点振速的重建误差,基于质点振速—质点振速的重建误差要小于基于声压—声压的重建误差。
图12为不同频率下基于声压—声压重建的误差曲线图,图13表示不同频率下基于质点振速—质点振速重建的误差曲线图。我们可以看出在不同的激励频率下,剔除散射的重建误差要明显小于忽略散射的重建误差,所以在声场分离时必须考虑散射声场的影响,将散射声场从目标源声场中剔除以减小目标声源的重建误差。进一步观察可以得出基于质点振速—质点振速的重建误差要小于基于声压—声压的重建误差,随着激励频率的增大重建误差有增大趋势,这是由于激励频率增大波长变短,在测量面位置不变的情况下获得的有用的声场信息减少,从而导致重建误差增大。
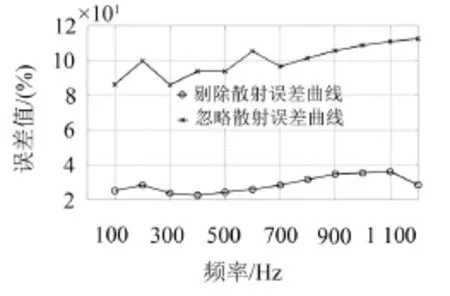
图12 不同频率下声压重建误差曲线图
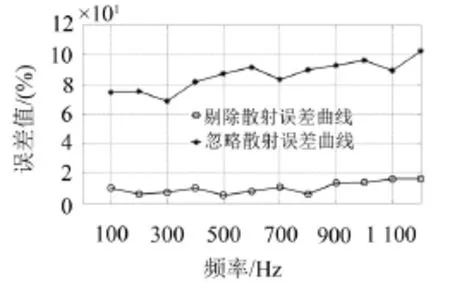
图13 不同频率下振速重建误差曲线图
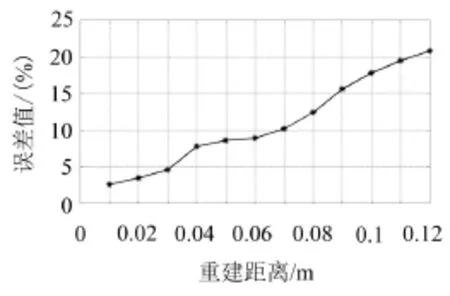
图14 不同重建距离误差曲线图
图14表示的是600 Hz时基于质点振速—质点振速的不同重建距离误差曲线图。
随着重建距离增大,重建误差也逐渐增大,其原因是由于随着测量面距离增大倐逝波的信息获取减少所致[13]。
3 结语
(1)由传递函数性质分析可知,在信噪比较小的情况下,由于高波数区域的噪声成分在计算过程中被放大从而导致有用信息被淹没,所以很容易会导致目标源声场分离及重建的失败,此时需要滤波器进行消噪处理。由于计算中存在的奇异性问题,采用K空间抽样法会造成很大的误差,而采用K空间积分法及平均值法则能够改善辐射圆上的奇异性问题,降低重建误差。随着重建距离的增大,获取的有用的声场信息减少且由于重建距离越大高波数区域的噪声放大倍数越大,从而造成重建误差增大。
(2)数值仿真表明,在复杂声场环境下运用常规的单面声场分离技术忽略散射声场的影响很难分离及重建目标声源的声场,而运用本文研究的理论同时剔除散射声场及干扰源声场的影响后大大提高了目标声源声场的重建精度。在复杂声场环境下基于质点振速—质点振速的重建效果优于基于声压—声压振速的重建效果,重建误差随重建距离增大而增大。
[1]于飞,陈剑,陈心昭.双全息面声场分离技术及其在近场声全息中的应用[J].声学学报,2003,28(5):385-389.
[2]于飞,陈剑,毕传兴,等.双全息面声场分离技术的实验研究[J].声学学报,2005,30(5):452-456.
[3]于飞,陈剑,李卫兵,等.单全息面声场分离技术及其在近场声全息中的应用[J].机械工程学报,2004,40(2):112-116.
[4]WU S F.Hybrid near-field acoustic holography[J]. Journal of the Acoustics Society of America,2004,115(1):207-217.
[5]毕传兴,张永斌,徐亮,等.基于双面质点振速测量的声场分离技术[J].声学学报,2010,35(6):653-658.
[6]毕传兴,张永斌,徐亮,等.基于声压-振速测量的平面近场声全息实验研究[J].物理学报,2010,59(2):1108-1115.
[7]毕传兴,唐琦,张永斌,等.双面Patch近场声全息实验研究[J].合肥工业大学学报,2011,34(3):321-325.
[8]金莉萍.基于格林函数的典型声场反演技术[D].哈尔滨:哈尔滨工程大学,2008.
[9]BRAIKIA Y,MELON M,LANGRENNE C,et al. Evaluation of a separation method for source identification in small spaces[J].Journal of the Acoustics Society of America,2013,134(1):323-331.
[10]WILLIAMS E G.Fourier acoustic:Sound radiation and near-field acoustic holography[M].London:Cambridge University Press,1999.
[11]聂佳.基于主动声全息的全向声反射系数测量方法的理论仿真及实验研究[D].哈尔滨:哈尔滨工程大学,2005.
[12]张永斌,徐亮,毕传兴,等.基于声压-振速测量的单面声场分离技术[J].物理学报,2009,58(12):8364-8371.
[13]陈心昭,毕传兴.近场声全息技术及其应用[M].北京:科学出版社,2013.
Reconstruction Errors of Sound Fields of Target Sound Sources under Complex Sound Field Environment
ZHANG Shi-ke1,2,ZHU Hai-chao1,2,XIE Zhi-min3,MAO Rong-fu1,2
(1.Institute of Noise and Vibration,Naval University of Engineering,Wuhan 430033,China;2.National Key Laboratory on Ship Vibration and Noise,Wuhan 430033,China;3.Marine Environment Project Office of PLA,Beijing 100081,China)
Aiming at the problem that sound field reconstruction of target sound sources can be disturbed easily,a new separation and reconstruction calculation method of the target sound sources based on single-side sound-field separation technique is presented under mixed sound field environment.This mixed sound field consists of interference source sound field,scattering sound field and target sound field itself.First of all,the influence of the interference sound source field and the scattering sound field is cleared by theoretical analysis and formula deduction.Then,the separation and reconstruction errors of the sound field are analyzed by using transfer function property and the singularity in the calculation formula is eliminated.Finally,the high resolution sound field reconstruction image is obtained.Numerical simulation shows that the conventional single surface sound field separation technique can hardly reconstruct the sound field of the target sound source under the mixed sound field environment.While the sound field of the target sound source can be reconstructed very well by using the proposed separation and reconstruction method.And the accuracy of the sound field reconstruction is improved.
acoustics;acoustic holography;complex sound field;reconstruction of sound field;error analysis
TB532
ADOI编码:10.3969/j.issn.1006-1335.2016.05.005
1006-1355(2016)05-0021-05+45
2016-03-28
张诗科(1990-),男,山东省菏泽市人,硕士生,主要研究方向为振动与噪声控制。E-mail:15527973386@163.com
朱海潮(1963-),男,博士生导师。E-mail:haiczhu@163.com

