带横向裂纹的拉杆转子非线性动力学特性研究

胡　亮，柳亦兵，徐晓星，陈昀丛

（1.华北电力大学 能源动力与机械工程学院，北京 102206；2.神华河北国华定州发电有限责任公司，河北 定州 073000）

带横向裂纹的拉杆转子非线性动力学特性研究

胡亮1，柳亦兵1，徐晓星1，陈昀丛2

（1.华北电力大学 能源动力与机械工程学院，北京 102206；2.神华河北国华定州发电有限责任公司，河北 定州 073000）

以拉杆转子为对象，对具有横向裂纹的拉杆转子非线性动力学响应特性进行研究。基于达朗贝尔原理建立考虑轮盘之间非线性接触特性的裂纹拉杆转子系统运动方程。采用数值积分方法对运动方程进行求解，得到轮盘振幅随转速变化的曲线。分析裂纹刚度减小量、轮盘质量偏心矢量夹角、接触面阻尼系数、裂纹角等系统参数对轮盘幅频特性的影响。同整体转子相比，裂纹拉杆转子除在1/2阶、1/3阶临界转速附近发生1/2阶、1/3阶亚谐共振外，在超临界转速区域存在超谐共振。系统参数对裂纹拉杆转子幅频特性曲线影响较大。分析结果可为认识裂纹转子系统的响应特性、开展裂纹转子的故障诊断提供理论指导。

振动与波；拉杆转子；亚临界共振；超临界共振；幅频特性曲线；达朗贝尔原理

裂纹故障是旋转机械常见的故障之一。造成裂纹故障的原因包括转子本身材料的缺陷、转子疲劳以及意外的冲击等。裂纹故障特征识别比较困难，工程中如果任由裂纹发展会导致严重的工程事故。开展裂纹转子的动力学特性、裂纹转子的故障特征提取方法研究具有重要的工程意义。国内外学者对裂纹转子进行了大量的研究，目前研究主要集中在裂纹刚度模型的描述以及裂纹转子动力学响应两个方面［1-5］。褚福磊等对现有裂纹刚度模型进行总结，提出了一种新的裂纹刚度模型能更好地反映裂纹转子刚度的变化规律［6］。陈铁锋等通过有限元方法建立了双裂纹转子系统的动力学模型，研究了不同裂纹角的转子动力学行为，并与实验结果进行对比，验证了模拟的有效性［7］。Sinou等通过实验研究了裂纹转子的非线性振动特性［8］。钟志贤等基于Rayleigh方法计算得到了裂纹轴单元的刚度模型，基于有限元方法建立具有横向裂纹的多盘柔性转子系统的数学模型，研究了裂纹对系统动力学特性的影响［9］。

已有的关于裂纹转子的动力学特性及故障诊断的研究多是针对整体转子。拉杆转子在航空发动机及重型燃气轮机中应用广泛。拉杆转子由轴向拉伸的拉杆将各轮盘压紧组成，系统中存在大量的接触面。张子阳等建立了拉杆转子盘与盘之间的接触力学模型，采用融合算法对盘与盘之间的接触刚度进行修正，并通过实验对修正算法进行了验证［10-11］。袁奇等通过引入弹簧连接单元对变截面轴段和接触界面刚度削弱进行模化，通过改方法得到的特征频率与实验结果相吻合［12］。何鹏等搭建拉杆转子试验台，研究了不同预紧力作用下临界转速的变化规律，结果表明随着预紧力的增大前两阶临界转速升高［13］。

文献［14］建立的整体转子模型，没有考虑轮盘之间的非线性恢复力。

从以上分析可知，盘与盘之间的接触对拉杆转子的响应特性影响较大。拉杆转子响应问题分析不同于整体转子，当转轴有裂纹时，对振动响应特性可能产生不同的影响，但是相关的研究不多。本文建立了具有横向裂纹的拉杆转子的动力学模型，得到了转子振幅随转速的变化曲线。分析了裂纹刚度减小量、偏心矢量夹角、接触阻尼以及裂纹角对曲线的影响，可为认识裂纹转子系统的响应特性、开展裂纹转子的故障诊断提供理论指导。

1　物理模型和运动方程

图1为具有横向裂纹的拉杆转子结构示意图。拉杆转子两端采用刚性支承，裂纹位于左侧无质量弹性轴的中部，轮盘之间通过拉杆连接。两轮盘的质量分别为m1、m2，质量偏心分别为e1、e2，两轮盘质量偏心之间的夹角为φ，无裂纹时轴的刚度为k0，轴的结构阻尼系数为c，轮盘接触面的阻尼系数为c1。

图1　拉杆转子示意图

1.1裂纹模型

图2为裂纹截面及转角示意图。裂纹刚度模型主要描述转轴转角对裂纹轴动态刚度变化的影响规律。

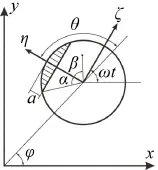
图2　裂纹截面示意图

假设转轴在无裂纹时的刚度为k0，裂纹全部张开时转子的刚度减少量为Δk，在旋转坐标系下，转子的刚度表示为

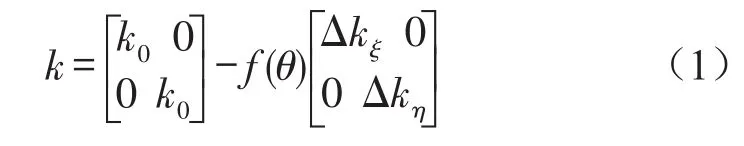
f（θ）为开关函数，θ=ωt+β+φ，ω为轴转速，β为转子裂纹方向与质量偏心之间的夹角，φ为初始相位。

经坐标变换，得到固定坐标系下裂纹刚度的矩阵

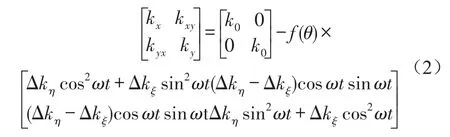
忽略ζ方向裂纹刚度的变化量，令Δkζ=0，得到

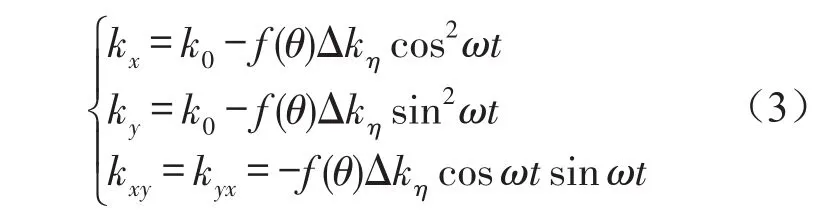
从上式可以发现，由于裂纹的存在，轴在x、y方向的刚度出现交叉。

本文采用余弦模型表征裂纹的开闭过程，开关函数f（θ）的表达式为［14］

1.2动力学方程

图3为轮盘坐标示意图，Fx1、Fy1、Fx2、Fy2为接触层的非线性恢复力，其表达式可以表示为如式（5）所示［15］。

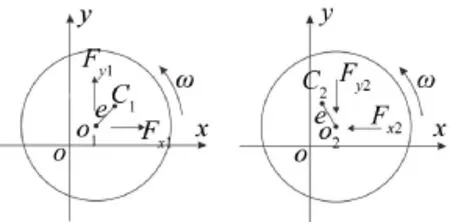
图3　轮盘坐标

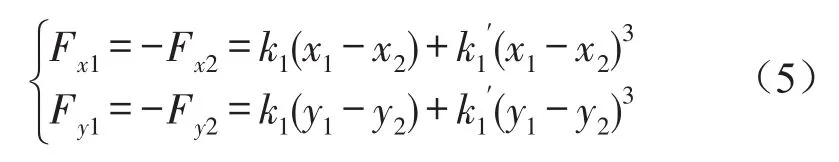
根据达朗贝尔原理建立系统的运动方程式

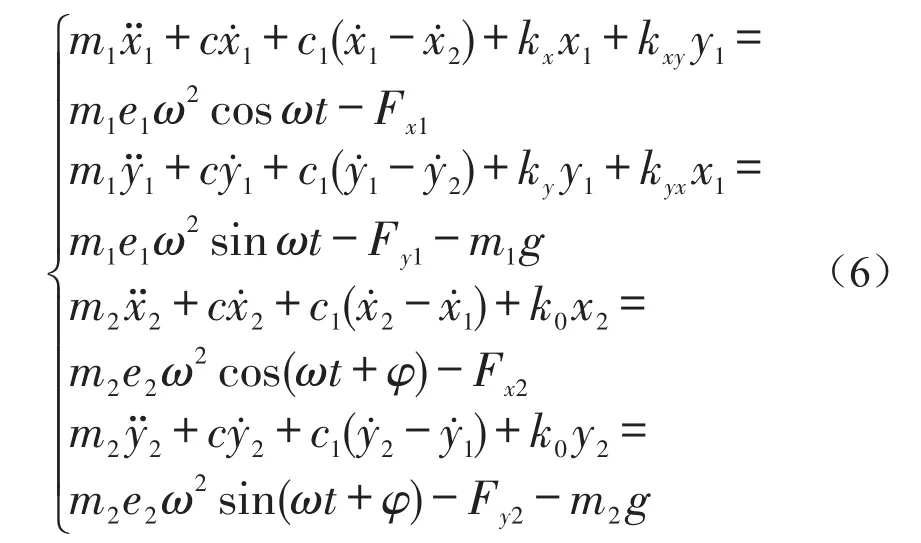
定义无量纲变量

Xi=xi/s，Yi=yi/s，s=m1g/k0，τ=ωt。将其代入式（6）得到裂纹拉杆转子系统的无量纲方程

2　数值计算结果及讨论

轮盘之间接触的存在使裂纹拉杆转子响应更加复杂。拉杆转子系统参数如表1所示。

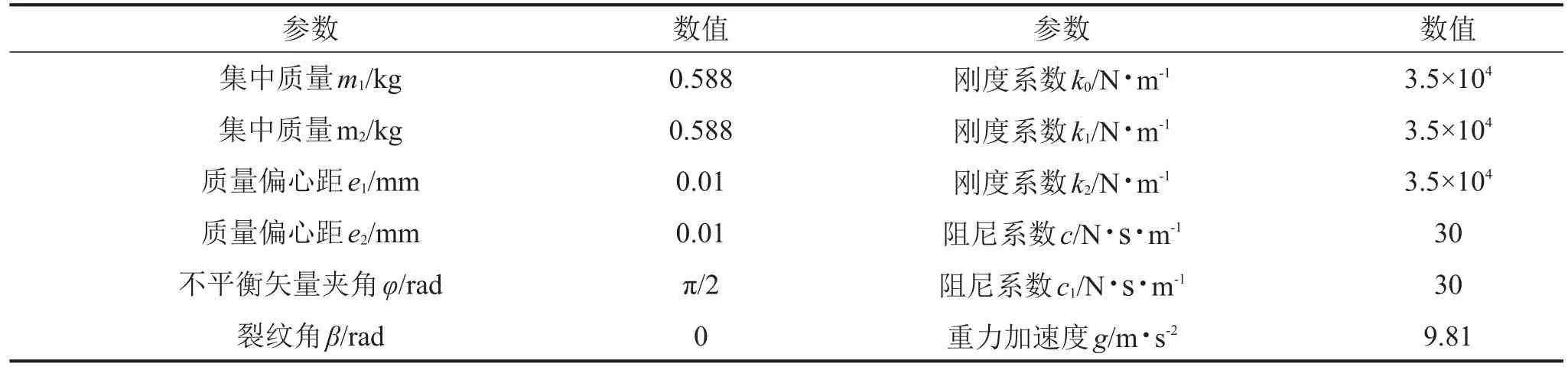
表1　裂纹拉杆转子系统参数

2.1裂纹刚度减小量的影响

图4为不同Δkη时整体转子轮盘振动幅值随转速变化曲线。

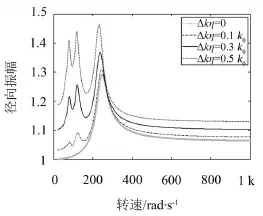
图4　整体转子轮盘振动幅值随转速变化曲线

从图4可以看出，4种不同情况下转子系统对应的1阶临界转速分别为247 rad/s，243 rad/s，234 rad/s和230 rad/s。随着η方向裂纹转子刚度的减小量不断增大，转子系统的1阶临界转速不断减小，其原因是裂纹导致转子系统刚度降低从而引起系统固有频率下降。Δkη很小时，在1/2以及1/3临界转速附近出现了一个很小的峰值，系统发生1/2、1/3亚谐共振。随着Δkη增大，1/2、1/3亚谐共振幅值不断增大，在Δkη=0.5 k0时，1/2、1/3亚谐共振幅值几乎达到临界转速共振峰值。

图5示出Δkη取不同值时，拉杆转子轮盘振动幅值随转速变化曲线。与图4进行对比可以发现，裂纹拉杆转子系统响应曲线中出现了一些新的特征。拉杆转子系统除了在临界转速处有共振峰值外，在超临界转速区域也存在一个共振幅值，这是整体转子系统中没有的现象。随着Δkη的变化，超临界共振峰值始终存在。同时，裂纹拉杆转子在1/2以及1/3临界转速附近仍出现了共振幅值。

2.2偏心矢量夹角的影响

取Δkη=0.3 k0，改变质量偏心之间的矢量夹角φ值，拉杆转子系统其它基本参数见表1。图6示出矢量夹角为0、π/2和π值时，拉杆转子轮盘振动幅值随转速变化曲线。

从图6可以看出不平衡量之间夹角对轮盘振动幅频特性曲线影响较大。φ=0时，由于两轮盘不平衡质量相等，两轮盘不发生相对移动，系统响应曲线与整体转子相似，超临界共振峰值消失；φ=π/2时，1/2阶、1/3阶亚谐共振与超临界共振同时出现；φ=π时，1/2阶、1/3阶亚谐共振以及超临界共振峰值依然存在，但是临界转速附近峰值急剧减小，主要是由于两轮盘不平衡质量相差180°，拉杆转子系统整体不平衡质量达到最小，在临界转速处的峰值降低。

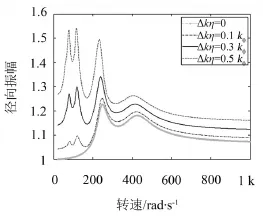
图5　拉杆转子轮盘振动幅值随转速变化曲线

图6　不同矢量夹角φ拉杆转子轮盘振动幅值随转速变化曲线

2.3阻尼的影响

取Δkη=0.3 k0，改变轮盘接触面阻尼系数c1值，拉杆转子系统其它基本参数见表1。图7示出c1=30 N·s/m、c1=50 N·s/m和c1=70 N·s/m时，拉杆转子轮盘振动幅值随转速变化曲线。

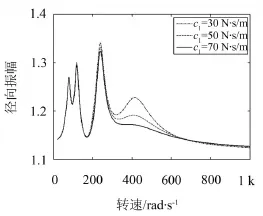
图7　不同阻尼系数c1拉杆转子轮盘振动幅值随转速变化曲线

从图7可以发现阻尼系数c1对于超临界共振峰值具有很好的抑制作用，对1/2阶、1/3阶亚谐共振以及临界转速附近共振峰值影响较小。增大阻尼系数c1，超临界共振峰值逐渐减小，在c1=70 N·s/m时，超临界共振基本消失。

2.4裂纹角的影响

取Δkη=0.3 k0，改变裂纹角β值，拉杆转子系统其它基本参数见表1。图8示出β=π/2和φ=π时，拉杆转子轮盘振动幅值随转速变化曲线。

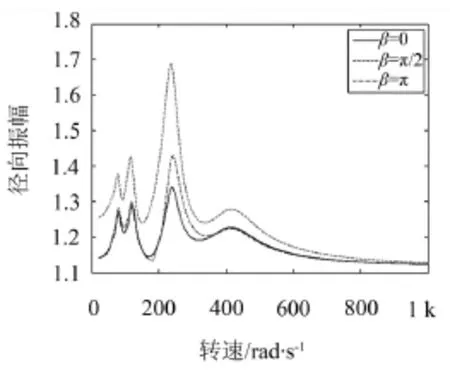
图8　不同裂纹角β值拉杆转子轮盘振动幅值随转速变化曲线

从图8可以看出，裂纹角β主要影响共振峰值。在β=π/2时，1/2阶、1/3阶亚谐共振、临界转速共振以及超临界共振峰值达到最大。

3　结语

本文采用数值积分方法对裂纹拉杆转子的非线性动力学响应特性进行研究。讨论裂纹刚度减小量、接触面阻尼系数、轮盘矢量夹角以及裂纹角对系统幅频特性曲线的影响，并与整体转子进行对比。通过分析得出如下结论：

（1）与整体转子相比，裂纹拉杆转子除在1/2阶、1/3阶临界转速附近发生1/2阶、1/3阶亚谐共振外，在超临界转速区域存在超谐共振；

（2）Δkη较小时，1/2阶、1/3阶亚谐共振并不明显，随着Δkη的增大，1/2阶、1/3阶亚谐共振峰值明显增大，在Δkη=0.5 k0时，1/2阶、1/3阶亚谐共振峰值超过临界转速共振峰值。增大Δkη，临界转速共振峰值以及超谐共振峰值增长并不明显；

（3）偏心矢量夹角φ主要影响临界转速共振峰值和超谐共振峰值，对1/2阶、1/3阶亚谐共振峰值影响较小。φ=0时，临界转速共振峰值增大，超谐共振消失；φ=π时，拉杆转子系统整体不平衡质量达到最小，在临界转速处的峰值降低；

（4）轮盘接触面阻尼系数c1主要影响超谐共振峰值，当c1增大到一定程度后，超谐共振消失；

（5）裂纹角β值主要影响1/2阶、1/3阶亚谐共振、临界转速共振以及超谐共振峰值。

［1］KULESZA ZBIGNIEW.Dynamic behavior of cracked rotor subjected to multisine excitation［J］.Journal of Sound and Vibration，2014，333（5）:1369-1378.

［2］SILANI M，ZIAEI-RAD S，TALEBI H.Vibration analysis of rotating systems with open and breathing cracks［J］. Applied Mathematical Modelling，2013，37（24）:9907-9921.

［3］李宁，程礼，陈雪峰.转轴上裂纹在通过临界转速过程中的呼吸特性［J］.噪声与振动控制，2010，30（2）：88-91.

［4］于海，陈予恕，曹庆杰.多自由度裂纹转子系统非线性动力学特性分析［J］.振动与冲击，2014，33（7）：92-98.

［5］谢平，杜义浩.基于信息嫡的裂纹转子动力特征分析与诊断方法［J］.机械工程学报，2009，45（1）：195-199.

［6］林言丽，褚福磊.裂纹转子的刚度模型［J］.机械工程学报，2008，44（1）：114-120.

［7］陈铁锋，荆建平，孟光，等.双裂纹转子振动特性的有限元和实验研究［J］.噪声与振动控制，2010，30（5）：15-19.

［8］SINOU JEAN-JACQUES.Experimental study on the nonlinear vibrations and n×amplitudes of a rotor with a transverse crack［J］.Journal of Vibration and Acoustics，2009，131（4）:041008.

［9］钟志贤，祝长生.横向裂纹多盘柔性转子系统的动力学特性［J］.浙江大学学报（工学版），2012，46（10）：1839-1845+1886.

［10］张子阳，谢寿生，钱征文，等.拉杆结构非线性接触的刚度融合修正方法［J］.汽轮机技术，2011，53（4）：249-252+ 256.

［11］张子阳，谢寿生，钱征文，等.拉杆结构中弹簧刚度和有限元模型刚度融合修正方法研究［J］.振动与冲击，2011，30（11）：53-56.

［12］高进，袁奇，李浦，等.燃气轮机拉杆式转子的刚度模化和模型修正方法［J］.西安交通大学学报，2013，47（5）：18-23.

［13］何鹏，刘占生，黄飞淋，等.拉杆转子临界转速随拉紧力变化规律试验［J］.振动测试与诊断，2014，34（4）：644-649+775.

［14］朱厚军，赵玫，王德洋.Jeffcott裂纹转子动力特性的研究［J］.振动与冲击，2001，20（01）：3-6+94.

［15］MAYES I W，DAVIES W G R.Analysis of the response of a multi-rotor-bearing system containing a transverse crackinarotor［J］.ASMEJournalofVibration，Acoustics，Stress，and Reliability in Design，1984，106: 139-145.

Nonlinear Dynamic Response of a Rod Fastening Rotor with a Transverse Crack

HULiang1，LIU Yi-bing1，XU Xiao-xing1，CHEN Yun-cong2
（1.School of Energy，Power and Mechanical Engineering，North China Electric Power University，Beijing，102206，China；2.Guohua Dingzhou Power Generation Co.Ltd.，Dingzhou 073000，Hebei China）

The dynamic response of a rod fastening rotor with a transverse crack is investigated.The dynamic equations of the system are derived by using D’Alembert principle.Numerical integration method is used to solve the equations and the amplitude-frequency curve of the system is obtained.The effects of system parameters such as the stiffness reduction，mass centroid eccentricity，damping coefficient of the contact surface and the crack angle on the amplitudefrequency curve are discussed.Compared with integral rotor，besides the 1/2 and 1/3 order sub-harmonic resonances，superharmonic resonance is discoved in the cracked rod fastening rotor system.System parameters have a great influence on the system amplitude-frequency curve.These results can provide the guidance for the fault diagnose of cracked rod fastening rotors.Meanwhile，the study may have some significance for further understanding of the nonlinear dynamic characteristics of cracked rod fastening rotors.

vibration and wave；rod fastening rotor；sub-harmonic resonance；super-harmonic resonance；amplitudefrequency curve；D’Alembert principle

O422.6

ADOI编码：10.3969/j.issn.1006-1335.2016.05.003

1006-1355（2016）05-0011-04+20

2016-03-12

北京市共建项目资助项目（ZDZH20141005401）；中央高校基本科研业务费专项资金资助项目（2014MS11）

胡亮（1988-），男，博士研究生，主要研究方向为旋转机械动力学特性分析。E-mail:liang_h@ncepu.edu.cn

柳亦兵，男，博士生导师。E-mail:lyb@ncepu.edu.cn