振动试验机电传递函数的结构动特性分析

夏江宁，宋汉文

（1.同济大学 航空航天与力学学院，上海 200092；2.北京强度环境研究所 环境可靠性中心，北京 100076）

振动试验机电传递函数的结构动特性分析

夏江宁1，2，宋汉文1

（1.同济大学 航空航天与力学学院，上海 200092；2.北京强度环境研究所 环境可靠性中心，北京 100076）

在振动试验中，应用试验件与振动台台面组成大系统的建模方法，建立振动台的台面控制加速度与驱动电压之间的机电传递函数，分析试验件固支模态频率与机电传递函数零点体系之间的对应关系，当将振动控制仪的驱动电压看作为整个系统的广义激励时，试验件的固有频率可以在只有台面控制加速度的情况下得到辨识。最后以π形钢梁的振动试验结果验证了该方法的正确性。

振动与波；振动试验；机电传递函数；固支模态频率；驱动电压

结构动力学试验主要包括模态试验和振动试验，两者有着明确的应用范围和试验目的。模态试验基于小变形假设建立了响应与激励之间的传递关系，进而辨识结构的动特性；振动试验模拟试验件的真实振动环境，通过基础激励的方式考核结构的环境适应性。但是，两类试验在分析手段、测试设备、信号处理等方面有着相同的工程应用，当将基础加速度看作为系统激励，建立试验件加速度响应与基础加速度之间的传递函数，进而可辨识结构的动特性。20世纪80年代以来，利用振动试验数据开展动特性的研究主要集中在固支模态参数辨识［1-2］、自由模态参数识别［3-4］、有限元模型修正［5-6］。由于振动试验的激励量级与结构的实际工况相当，因此采用振动试验数据进行模态分析时，可以获得更加符合真实环境下的工作模态参数［7-8］。

电动振动台是目前应用最广泛的振动试验设备，通过电磁力驱动振动台的运动部件（也称为动圈或台面），并能够实现给定测点的运动可控性。在理论分析过程中，常以振动台的台面作为单自由度的机电耦合系统，分析电气特性对随机和正弦振动以及冲击信号控制响应精度的影响［9-11］以及在定电流和定电压条件下的振动台台面运动响应规律［12］。但是，对于安装了试验件的多自由度机电耦合系统，目前尚缺乏相关的理论分析和研究。

本文将多自由度的试验件与振动台台面组成的系统作为研究对象，建立了振动台台面控制加速度与动圈驱动电压之间的机电传递函数，分析了试验件的结构动特性与机电传递函数之间的对应关系，获得了在不采集试验件运动响应情况下辨识试验件固有频率的方法。

1　多自由度离散系统的振动试验模型

多自由度离散系统（即试验件）与振动台运动部件组成的大系统力学模型如图1所示。

图1　振动试验的机电耦合模型图

虚线框内的系统为多自由度的试验件，Mb为振动台台面，fb为振动台的电磁力，Kb和Cb分别为振动台运动部件与地基之间的连接刚度和连接阻尼，电气回路由电感、电阻和等效电压组成。

n自由度离散系统与单轴振动台的动力学频域方程为

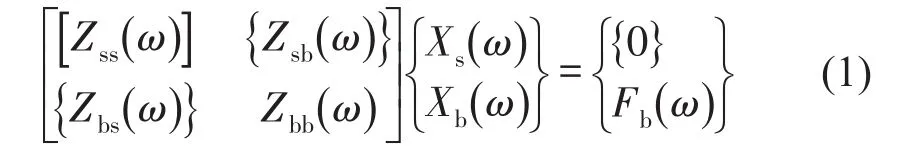
振动台系统的电路方程为

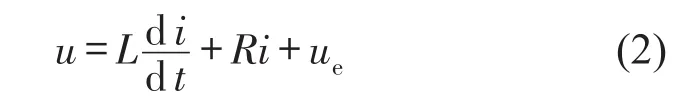
其中u为动圈电压（也称为输入电压），R为等效电阻，L为等效电感，ue=Blẋb为振动台的等效电压。

联立式（1）和式（2），可得台面加速度与电磁力之间的表达式为

将式（1）所示的阻抗矩阵按照试验件和振动台台面进行分块，并根据分块矩阵求逆公式［13］可得

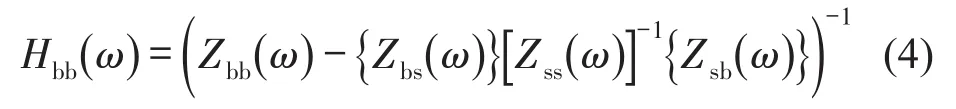
式中的Hbb（ω）为振动台台面的原点频响函数。

联立式（3）和式（4），则台面加速度与驱动电压之间的机电传递函数的幅值表达式可写为

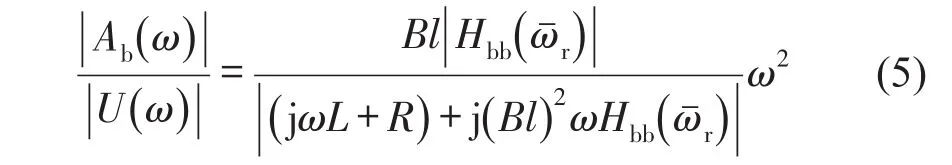
根据式（5）可知，振动试验的机电传递函数反映了大系统与电气回路的耦合特性。其中，台面原点频响函数决定了机电传递函数的零点集，而电气参数与台面原点频响函数共同影响传递函数的极点特性。本文只研究机电传递函数的零点特性。

依据式（1）中机械阻抗的分块矩阵，可知台面原点频响函数［14］为

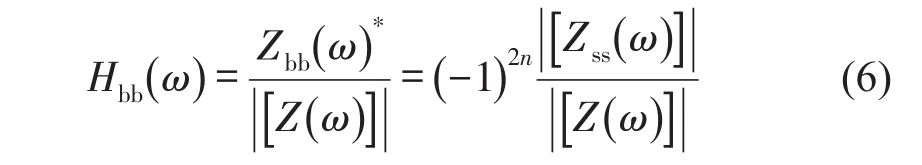
根据式（5）和式（6）可知：机电传递函数的零点取决于振动台台面原点频响函数的零点，而振动台台面原点频响函数零点对应着试验件的极点。因此，可以认为机电传递函数幅频曲线的极小值对应着试验件的固有频率。

2　试验验证

试验件为π形钢梁，粱长1 200 mm，立柱高400 mm，梁和立柱的板厚为10 mm，下部为两层厚度为20 mm钢板，其外形及传感器布置和试验方向定义如图2所示。图中，A表示加速度传感器，数字为传感器编号。

图2　试验件及测点布置图

试验类型为正弦扫描振动试验，采用传统的加速度控制方式，以台面加速度传感器为控制点，控制策略为A11和A12的两点平均控制，振动量级为恒加速度0.1 g的平直谱，正弦振动试验的参考谱如图3所示。

图3　正弦扫描振动试验参考谱

π形梁的底部钢板通过6×Φ14螺钉直接与振动台台面和水平滑台相连接，试验件在三个方向的安装状态如图4所示。

图4　试验件的三个方向安装状态图

振动试验中，振动控制仪以两个控制传感器经过平均后的信号作为台面控制加速度，并使之参与闭环反馈控制过程，通过与给定参考谱的比较修正，最终获得输出驱动电压信号。本文将振动控制仪的控制加速度与驱动电压信号作为机电传递函数，给出其双对数坐标下的幅频图（如图5所示）。

图5　机电传递函数的幅频图

由于振动控制仪的控制加速度与驱动电压等信号的数据保持格式为自功率谱，因此本文不考虑机电传递函数的相位信息。

根据图（5）可知，（1）机电传递函数的幅值与振动频率在中低频范围（5 Hz～150 Hz）内呈现明显的幂函数关系；（2）三个方向的响应曲线上均有明显的极小值；（3）单轴振动试验都激发出各自敏感的模态；（4）除了X向的48.56 Hz的谷值之外，其他响应曲线的谷值之后紧接着存在峰值，呈现出谷峰交替出现的现象。

对π形钢梁分别进行振动试验和模态试验，根据机电传递函数与固支频率响应函数获得的辨识结果对比情况如表1所示。

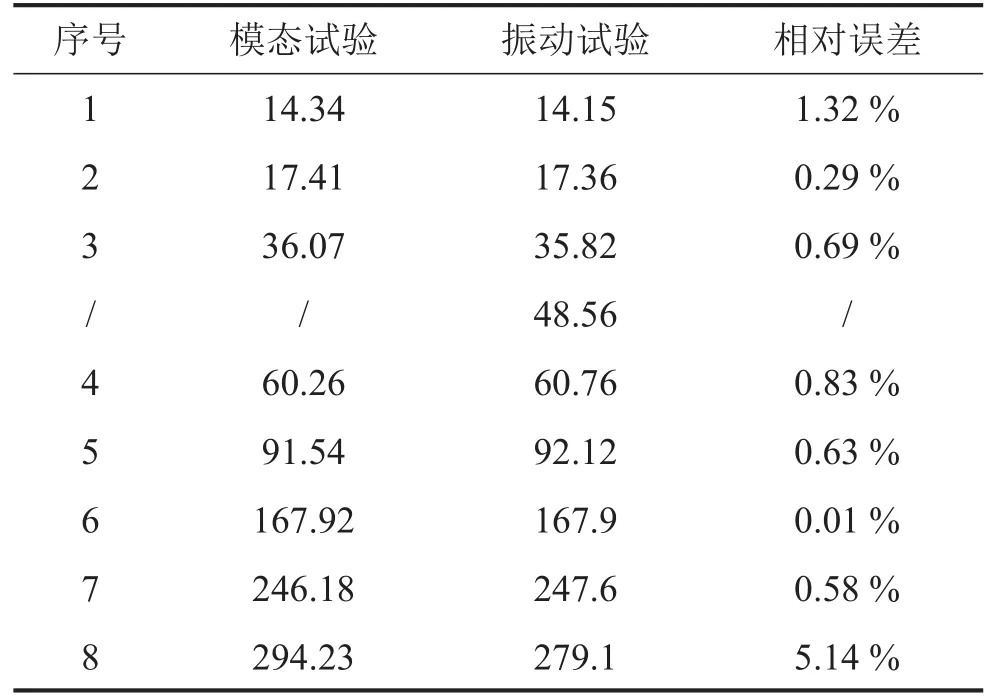
表1　π形梁的固有频率对比

根据表1可知，机电传递函数识别π形梁的固有模态频率有着很高的精度，前8阶固有频率的相对误差均小于6%。但是，X向固有频率比模态试验辨识值多了1阶固有频率（48.56 Hz）。根据图5所示的响应曲线在试验件固有频率附近出现谷峰交错的规律，可以排除48.56 Hz为X向固有频率。

3　结语

振动试验过程中，当将驱动电压信号作为试验件的广义激励时，建立控制加速度与驱动电压的机电传递函数后，可识别试验件在固支状态下的固有频率。也就是说，在不采集试验件响应信号的情况下，只需要知道控制仪的控制谱和驱动谱就可以获得试验件的固支模态频率。

［1］BÉLIVEAU J G，VIGNERON F R，SOUCY Y，et al. Modalparameterestimationfrombaseexcitation［J］. Journal of Sound and Vibration，1986，107（3）:435-449.

［2］夏江宁，陈志峰，宋汉文.基于动力学环境试验数据的模态参数识别［J］.振动与冲击，2006，25（1）：99-103.

［3］SINAPIUS J M.Identification of free and fixed interface normal modes by base excitation［C］//Proceedings-spie the internationalsocietyforopticalengineering.spie international society for optical，1996:23-31.

［4］SCHEDLINSKI C，LINK M.Identification of frequency response functions and modal data from base excitation tests using measured interface forces［C］//Proceedings of the ASME conference on noise and vibration，Boston. 1995.

［5］JAMSHIDI E，ASHORY M R.Comparative study of RFM and model updating method using base excitation test data［C］.Proceedings of the IMAX-XXVII，Orlando，2009.

［6］DONLEY M.Correlation of FE models to base excitation tests，Society for Experimental Mechanics，Inc，16 th International Modal Analysis Conference，Vol.2，1998，pp.959-964.

［7］王佐才，任伟新.基于解析模式分解的密集工作模态参数识别［J］.噪声与振动控制，2013，33（6）：18-24.

［8］静行，刘真真，原方.随机激励下基于ICA的结构模态参数识别［J］.噪声与振动控制，2014，34（6）：178-183.

［9］CHEN T H，LIAW C M.Vibration acceleration control of an inverted-fed electrodynamic shaker［J］.IEEE/ASME Transactions on Mechatronics，1999，4（1）:60-70.

［10］CHANG-MING LIAW，WEN-CHIN YU，THIN-HUO CHEN.Random vibration test control of inverter-fed electrodynamicshaker［J］.IEEETransactionson Industrial Electronics，2002，49（3）:587-594.

［11］郭继峰，任万滨，康云志，等.电动振动台模型辨识方法及其应用的研究［J］.振动与冲击，2011，30（7）：241-244.

［12］陈颖.三轴向振动台动力学参数识别与建模［D］.南京：南京航空航天大学，2012.

［13］ROGER A H，CHARLES R J.Matrix Analysis［M］. Cambridge University Press，1990，Chaps 0.7.3.

［14］傅志方，华宏星.模态分析理论与应用［M］.上海：上海交通大学出版社，2000：144.

Research on Structural Dynamic Characteristics Based on Electromechanical Transfer Function Using Vibration Test Data

XIA Jiang-ning1，2，SONG Han-wen1
（1.Tongji University，Shanghai 200092，China；2.Beijing Institute of Strength and Environment Engineering，Beijing 100076，China）

In vibration test，the electromagnetic force cannot be measured directly which driving the test components and the shaking table to achieve the given motion of the control transducer.When the output voltage of the vibration controller is considered as the generalized excitation of the vibration system，the natural frequency of the test components can be analyzed only in the case that the acceleration of the shaking table can be obtained.In this paper，a large system including test components and the shaking table is studied，and the electromechanical transfer function between the table acceleration and the output voltage of the vibration controller is obtained.The corresponding relation between the modal frequency of the test components in the clamped state and the zero-point system of the electromechanical transfer function is analyzed.Finally，the test results of a π-shaped steel beam verify the correctness of this technique.

vibration and wave；vibration test；electromechanical transfer function；clamped mode frequency；drive voltage

V216.2+1

ADOI编码：10.3969/j.issn.1006-1335.2016.05.040

1006-1355（2016）05-0192-04

2016-03-08

夏江宁（1976-），男，山东省泰安市人，博士生，主要研究方向为结构动力学及环境试验技术。

宋汉文，男，博士生导师。E-mail:hwsong@tongji.edu.cn