超声波测振信号的能量算子解调方法

曹青松，陈　刚，毕彬杰，周继惠

（华东交通大学 机电工程学院，南昌 330013）

超声波测振信号的能量算子解调方法

曹青松，陈刚，毕彬杰，周继惠

（华东交通大学 机电工程学院，南昌 330013）

连续超声波束遇到振动物体表面会产生多普勒效应，反射超声波信号是受振动信号调制的非线性调相信号。对反射波信号求导获得调幅调频信号，再采用能量算子对称差分法，求取该调幅调频信号的瞬时幅值及瞬时频率。鉴于超声波反射回波信号存在幅值衰减现象，而超声波频率不易受外界干扰，故通过调幅调频信号的瞬时频率提取被测物体的振动速度，并由振动速度求导得到振动加速度。同时，从幅值及频率两个方面探讨振动测量范围。仿真及实验结果表明：基于能量算子的超声波测振信号解调方法能有效地提取振动信号，与传统的相位解调方法相比，具有更大的测量范围。

振动与波；超声波；振动检测；能量算子；瞬时频率；解调

超声波振动测量是一种测量精度高、成本低的非接触振动测量方法，能够运用于高压、粉尘、强腐蚀等恶劣环境中或对轻质、细微结构进行非接触振动测量［1］。

在超声波振动测量中，反射超声波信号为相位被振动所调制的调相信号。为解调出被测物体的振动信号，Chereck针对该调相信号瞬时频率含有振动信息的特点，采用鉴频器提取调相信号的频率信息，通过频率信息获取振动速度［2］。Fernando等人将超声波发射信号及反射波信号转换成TTL波形，并进行异或处理，处理后的信号输入到低通滤波器中求得被测物体的振动信号［3］。Papageorgiou等人采用频率为40 kHz的窄脉冲超声波信号进行振动测量，通过频率计获取反射超声波的频率信息，并从获得的频率信息中提取振动信号［4］。YANG等人通过BASK调制方法将200 Hz、1 kHz的脉冲信号同时对40 kHz的脉冲载波信号进行调制，使发射探头发射该已调信号形式的超声波［5］。对其反射波信号进行处理，获取反射波的包络并重构不含载波的方波信号。将方波信号转换成TTL波形，通过数字相位计求得TTL波形相位变化，从中提取振动信号。上述振动信号解调方法可归纳为两种，第一种是通过求超声波发射信号及反射波信号的TTL波形相位差来获取振动信号；另一种是检测反射波信号的频率信息，从中提取振动信号。与第一种解调方法相比，第二种方法信号处理过程相对简单，系统成本更低。

能量算子是一种实现调制信号瞬时幅值和瞬时频率检测的重要方法，特别适用于信噪比较高、瞬时频率变化缓慢单分量信号瞬时频率的计算［6］。近年来，许多学者将其用于信号的解调分析，取得了良好的效果。程军圣等人采用能量算子解调方法对机械故障振动信号各个IMF分量进行解调处理，从而获得信号的幅值及频率信息，通过该幅值及频率信息有效地提取了机械故障振动信号的特征［7］。曾鸣等人通过归一化复域能量算子解调方法对转子碰摩故障信号进行解调，有效提取了该故障信号的瞬时频率［8］。

鉴于上述研究背景，本文提出采用能量算子对称差分法法对求导后的超声波测振信号进行解调处理，求得信号求导后的瞬时幅值及瞬时频率，再通过瞬时频率获取振动速度并求得振动加速度。最后通过仿真及实验来验证超声波测振信号能量算子解调方法的有效性及准确性。

1　超声波测振原理

超声波频率高，波长短，传播方向性好，在声阻抗差较大的固/气分界面会发生明显的反射现象。在空气中传播的连续超声波束遇到振动物体时，其相位会因多普勒效应而被振动所调制。

图1为超声波测振原理图，图中L为超声波探头与被测点处于平衡位置时的距离，φ为超声波的反射角，h为被测物体测点处的位移。

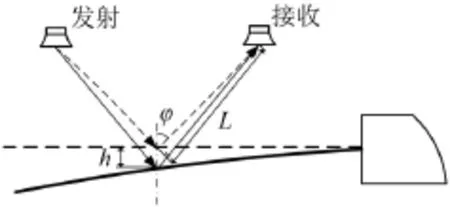
图1　超声波测振原理图

超声波发射探头发射的超声波可表示为

其中At为超声波的幅值，ω为超声波信号的频率。

由图1可知，当|h|max＜＜L时，超声波传播的距离L0为

因而，接收探头接收的反射波信号可表示为

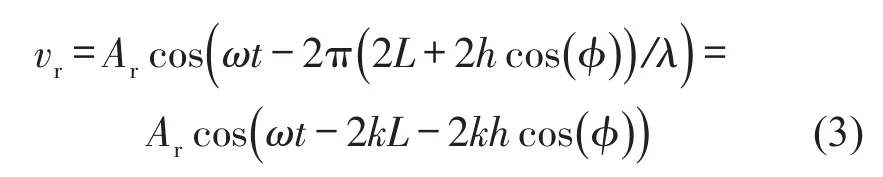
其中k=ω/c=2π/λ，c为超声波的声速，λ为超声波的波长，Ar为反射波信号幅值。

令被测物体测点处位移h为正弦信号，设为

其中h0为测点振动幅值，ωL为被测点振动频率。

由式（3）可知，反射超声波信号为相位被振动调制的调相信号。对式（3）求一阶导数得到含有瞬时幅值和瞬时频率的调幅调频信号，如式（5）所示

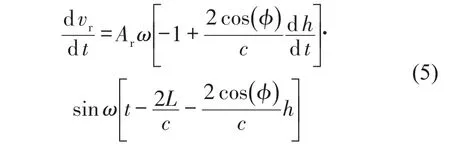
由上式可知，该调幅调频信号的瞬时幅值及瞬时频率均含有振动信息，对其进行解调处理便可得到振动信号。

2　超声测振信号的能量算子解调原理

2.1能量算子

能量算子是Teager在研究非线性语音建模时引入的用于分析和跟踪窄带信号能量的数学算法［6］。假设连续信号x（t）的能量算子定义为

对于做无衰减自由振动的线性振子，其位移x（t）=Acos（ωct+θ）的能量算子为

又知该线性振子的瞬时总能量是一个常数：E=m·（Aωc）2/2，m为振子质量；该能量与式（7）的运算结果仅差一常数因子m/2，因此算子Ψc称为能量算子。能量算子作用的结果反映并跟踪信号能量的变化。式（6）为连续信号能量算子，对于离散信号，能量算子采用差分定义

如果用离散时间变量nT代替连续时间变量t，其中T为采样周期，实际应用中一般归化为1，并用离散差分方程代替连续时间变量的导数，那么就可以得到时间连续信号能量算子Ψc与离散信号能量算子Ψd之间的映射关系。由差分方程的三种不同定义方式可以得到后向差分、前向差分、对称差分法三种映射关系，其中更为精确的对称差分法为［9］

2.2超声测振信号的能量算子解调原理

对反射超声波信号求导得到式（5）所示的调幅调频信号，该调幅调频信号可以写成

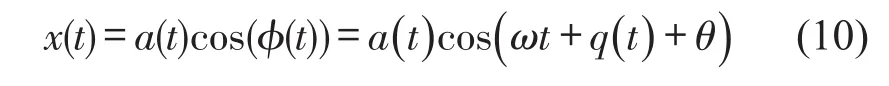
其中q（t）=-2ωhcos（φ）/c，θ=-2Lω/c。

该调幅调频信号瞬时幅值a（t）和瞬时频率ωi（t）分别为

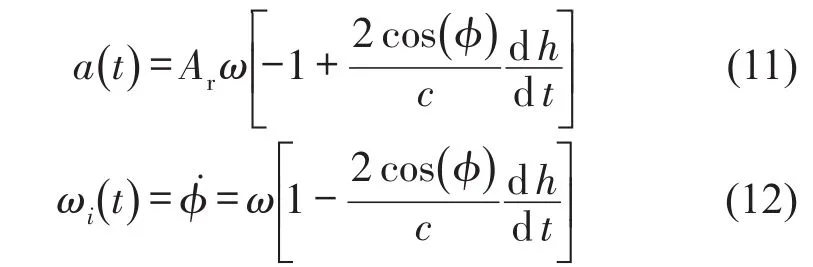
由式（11）、式（12）均可求得振动物体被测点处的振动速度dh/dt及振动加速度d2h/dt2。然而超声波在传播过程中存在吸收衰减和散射衰减，因而为保证测量精度，采用式（12）所示的瞬时频率求解振动物体被测点处的振动速度及振动加速度为求出调幅调频信号的瞬时幅值及瞬时频率，

采用能量算子法对式（10）进行处理

同理可得

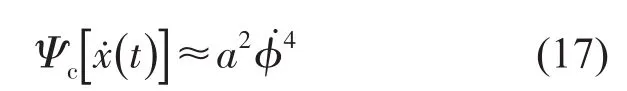
联立式（16）及式（17）得调幅调频信号的瞬时幅值及瞬时频率

式（18）及式（19）为连续时间能量算子表达式，对离散信号x（n）=a（n）cos［φ（n）］须利用所定义的离散时间能量算子及式（18）、式（19）中的对应关系。在此，采用更为精确的对称差分法方法即式（9），并结合式（18）、式（19）两式求得离散时间信号的瞬时频率及瞬时幅值公式

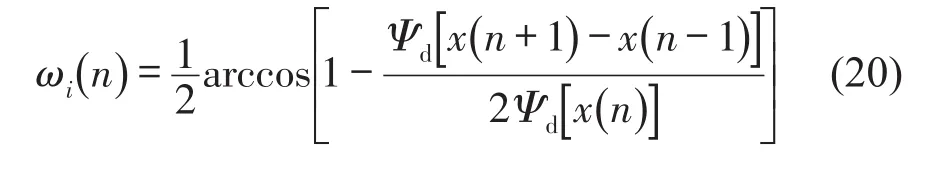
采用能量算子求得超声波测振信号的瞬时频率及瞬时幅值，结合式（13）、式（14）便可求出振动物体被测点处的振动速度及振动加速度。

2.3超声波振动测量范围的探讨

相位被振动物体所调制的反射超声波为调相信号，如式（3）所示。由于相位的变化范围为0～2π，若对式（3）所示调相信号直接进行鉴相处理解调出振动信号，超声波测振法所能测量的振动范围仅为0～λ/2，其中λ为超声波的波长。若超声波频率f=40 kHz，超声波的声速c=343 m/s，直接对反射波进行鉴相处理，超声波测振法的测振范围最大仅为4.3 mm。较小的测振范围严重制约了超声波测振法在非接触振动测量中的应用［3］。本文采用能量算子法对求导后的反射超声波信号进行解调处理，通过获取的瞬时频率来提取振动信号。该方法使测量范围突破了超声波波长的限制，为提高振动测量范围提供了新思路。本节从幅值及频率两个方面对基于能量算子的超声波振动测量方法测量范围进行探讨。

在超声波振动测量中，超声波的相位会因多普勒效应而被振动所调制。然而振动物体会向周围空气介质中辐射低频声波，当该低频声波与超声波在在介质中相遇时，超声波相位也会被该低频声波所调制［10］。若被测物体的振动频率fL＞4 000 Hz，只考虑多普勒效应对超声波相位的影响，振动测量结果将会存在较大误差［11］，因而在基于多普勒效应的振动测量中，被测物体的振动频率应低于4 000 Hz。在采用能量算子法对信号进行解调处理时，要求ωL＜＜ω，即fL＜＜f，其中ωL=2πfL，ω=2πf，fL为被测物体测量点处的振动频率，f为超声波频率，且f＞20 kHz。所以，基于能量算子的超声波振动测量方法所能测量的振动信号频率f0＜4 000 Hz。为保证如式（2）所示对超声波传播距离计算结果的准确性，要求h0=|h|max＜＜L，其中h、h0分别为被测物体测量点处的振动位移及位移幅值，L为超声波探头与被测点之间的距离。此外，在采用能量算子法解调超声波测振信号的过程中，为防止如式（5）所示的调幅调频信号因过调失真而导致测量结果不准确，应确保a（t）＞0或a（t）＜0即：h0＜c/2ωLcos（φ）。所以，基于能量算子的超声波振动测量方法所能测量的振动位移幅值h0＜c/2ωLcos（φ）且h0＜＜L。

若采用文献［12］中的参数，其中超声波频率f=40 kHz，超声波声速c=343 m/s，超声波反射角φ=8.5o，被测点振动频率ωL=2π×60 rad/s，则所能测量的振动位移幅值h0＜460 mm。令超声波探头与被测点处于平衡位置时的距离L＞＞460 mm，则基于能量算子的超声波振动测量方法所能测量的最大振动位移约为460 mm。而在相同参数条件下，对反射超声波信号直接进行鉴相处理解调出振动信号，所能测量的最大振动位移仅为超声波波长的一半，即4.3 mm。因而，采用基于能量算子的超声波振动测量方法能在一定程度上提高振动测量范围。

3　仿真研究

为检验能量算子对超声波测振信号解调的有效性及准确性，选取所设计的基于多普勒效应的超声波测振实验台参数［12］，采用40 kHz正弦形式的超声波信号作为测振信号，由式（5）得到仿真信号表达式为

其中，采样频率f=1 MHz，超声波探头与被测点处于平衡位置时的距离L=18 mm，h为被测物体测量点处振动位移，其表达式设为

对式（22）所示仿真信号采用能量算子法进行解调处理，得到仿真信号的瞬时幅值及瞬时频率，如图2、图3。

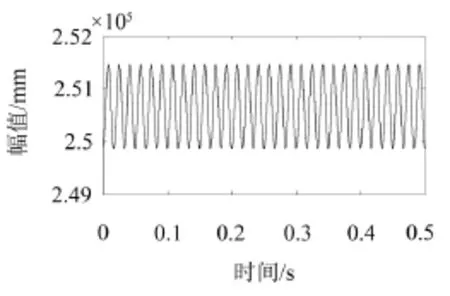
图2　仿真信号瞬时幅值

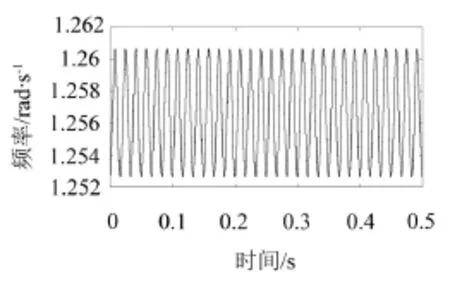
图3　仿真信号瞬时频率

将求得的瞬时频率代入式（13）、式（14）分别得到被测物体测量点处的振动速度及振动加速度。式（23）为被测物体测量点处实际振动位移，对其进行求导即可得到被测物体测量点处的实际振动速度和实际振动加速度。经能量算子解调得到的计算振动速度及物体测量点处的实际振动速度如图4所示，能量算子解调得到的计算振动加速度和物体测量点处的实际振动加速度如图5所示。

图4　振动速度

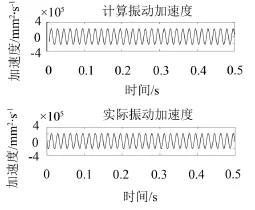
图5　振动加速度

由图4、图5可知，经能量算子解调得到的计算振动速度与实际振动速度、计算振动加速度与实际振动加速度基本一致。因而，采用能量算子法可以准确地求出被测物体测量点处的振动速度及振动加速度。

4　实验

采用基于多普勒效应的超声波测振系统实验台进行实验［12］，选取40 kHz正弦形式的超声波信号为测振信号，设置被测物体测量点以频率60 Hz，振幅1.5 mm的正弦形式振动，反射超声波的采样频率设为1 MHz。

采集的反射超声波信号为调相信号，求导后得到如图6所示的调幅调频信号。该调幅调频信号经能量算子法处理之后得到其瞬时幅值和瞬时频率，如图7、图8所示。

采用图8所示的瞬时频率求得振动速度及振动加速度，将得到的计算振动速度及计算振动加速度与被测物体测量点的实际振动速度及实际振动加速度进行比较，如图9、图10所示。

图6　调幅调频信号

图7　调幅调频信号瞬时幅值

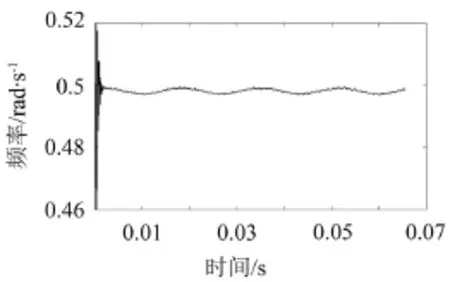
图8　调幅调频信号瞬时频率

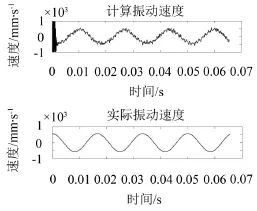
图9　振动速度

图10　振动加速度

由图9及图10可知，计算振动速度与实际振动速度的幅值及频率、计算振动加速度与实际振动加速度的幅值及频率均基本一致。所以采用能量算子法可有效地从超声波测振信号中解调出振动信号，解调所得结果比较准确。

5　结语

超声波测振信号是相位被振动调制的调相信号，对该信号求导得到瞬时频率和瞬时幅值均含振动信息的调幅调频信号。本文采用能量算子法实现该调幅调频信号的解调处理，获得其瞬时幅值及瞬时频率，通过瞬时频率求得振动速度及加速度。仿真及实验结果表明，能量算子法能够有效地解调出被测物体的振动速度及振动加速度，解调结果比较准确，该方法在一定程度上提高了振动测量范围。

［1］周月琴，行鸿彦.超声波远距离振动信号检测系统的设计［J］.机械科学与技术，2008，27（6）：819-821.

［2］CHERECK B.Contactless measurement of mechanical vibrationsbasedontheDopplereffect［J］.IEE Proceedings，1987，134（4）:339-342.

［3］FERNANDO F，ENRIQUE B.An ultrasonic ranging system for structural vibration measurements［J］.IEEE Transactions on Instrumentation and Measurement. 1991，40（4）:764-769.

［4］PAPAGEORGIOU C，KOSMATOPOULOS C，LAOPOULOS T.A method for remote measurement of velocity for vibration analysis［J］.IEEE International Conference on Electronics，Circuits&Systems.1999，3:1491-1494.

［5］YANG M H，HUANG K N，HUANG C F，et al.A high accurate ultrasonic measurement system for tremor using binary amplitude shifting-keying and phase-shift method［J］.BiomedicalEngineeringApplications，Basis& Comm-unication.2003，15（2）:61-67.

［6］高云鹏，李峰，陈婧，等.改进能量算子Nuttall窗频谱校正的闪变测量方法［J］.仪器仪表学报，2014，35（4）：745-753.

［7］程军圣，于德介，杨宇.基于EMD的能量算子解调方法及其在机械故障诊断中的应用［J］.机械工程学报，2004，40（8）：115-118.

［8］曾鸣，杨宇，郑近德，等.归一化复域能量算子解调及其在转子碰摩故障诊断中的应用［J］.机械工程学报，2014，50（5）：65-73.

［9］孟宗，李姗姗，季艳.基于对称差分能量算子解调的局部均值分解端点效应抑制方法［J］.机械工程学报，2014，50（13）：80-87.

［10］MATAR O B，REMENIERAS J P，PIZARRO L，et al. Performances of the parametric acoustic vibrometer for vibrationsensing［J］.IEEEUltrasonicsSymposium，1999，605-608.

［11］OLIVER B M，JEAN P R，CHRISTIAN B，et al.Noncontact measurement of vibration using airborne ultrasound［J］.IEEE Transactions on Ultrasonics，Ferroelectrics，and Frequency Control，1998，45（3）:626-632.

［12］周继惠，陈刚，曹青松，等.基于多普勒效应的超声波测振系统设计［J］.仪表技术与传感器，2015（7）：61-85.

Energy Operator Demodulation Method of the Ultrasonic Vibration Measurement Signal

CAO Qing-song，CHEN Gang，BI Bing-jie，ZHOU Ji-hui
（School of Mechanical and Electrical Engineering，East China Jiaotong University，Nanchang 330013，China）

A continuous ultrasonic beam is emitted towards the moving surface and the

ultrasound signal is phase modulated by vibration signal due to the Doppler Effect.The AM-FM signal is derieved from the derivative of the

ultrasound signal.The instantaneous frequency and instantaneous amplitude of the AM-FM signal are obtained through symmetrical difference of the energy operator demodulation.The amplitude attenuation of the

ultrasound signal is inevitable，but its frequency is not susceptible to external interference.So，the vibration speed of the object can be obtained from the instantaneous frequency of the AM-FM signal，and the vibration acceleration can be obtained from the derivative of the vibration velocity.The range of vibration measurement is discussed from the viewpoints of amplitude and frequency.Simulation and experiment results show that the energy operator demodulation method for the ultrasonic vibration measurement signal can effectively extract the vibration signal and this method has larger measurement range than the traditional phase demodulation method.

vibration and wave；ultrasonic；vibration measurement；energy operator；instantaneous frequency；demodulation

TB52+3

ADOI编码：10.3969/j.issn.1006-1335.2016.05.001

1006-1355（2016）05-0001-05

2016-01-28

国家自然科学基金资助项目（51265009）

曹青松（1978-），男，安徽无为人，博士，副教授，主要从事振动控制、无损检测等方面的研究。研究方向为振动控制、无损检测。E-mail:2000cqs@163.com