基于接收机位置信息的GNSS干扰源定位技术
靳睿敏,甄卫民
(中国电波传播研究所,山东 青岛 266107)
0 引 言
全球卫星导航系统(GNSS)已广泛地渗透应用到国家的很多基础设施的系统[1]以及个人应用中,与人们的生活息息相关.但是GNSS信号到达地面的功率很低,同时民用信号的格式是公开的[2],因此极易受到各种无意和人为故意的干扰,会对GNSS定位和授时的精度造成影响.
GNSS干扰在近些年引起了国际的广泛关注,及时地发现并消除GNSS干扰源,才能够保障GNSS在各个方面应用的性能.目前常用的干扰源定位方法是利用测向设备实现干扰源的交叉定位[3],但是在不知道干扰源的大致位置时,利用测向设备查找干扰源会耗费很长的时间.如果能够利用通用接收机的输出量实现干扰源的粗定位,将能为交叉定位提供初始参考位置和大概的查找范围.本文利用几乎所有的通用接收机都能输出的位置信息实现干扰源的粗定位.
1 GNSS干扰定位方法及算法分析
1.1 GNSS干扰定位方法
在实际应用中,随着用户的使用,很多通用接收机是移动的,如手机、车辆等上面的GNSS接收机.假设GNSS干扰源是固定的,随着接收机的移动,当逐渐逼近干扰源时,会造成接收机的失锁,此时,接收机的位置信息将丢失,当接收机逐渐地远离干扰源时,接收机又会重新获取位置信息.
对于通用接收机,接收机位置丢失点和重获取点处的干扰功率差是类似的,经过测试分析,通用接收机的位置信息丢失点和重获取点处的干扰功率差大约为5 dB.如果能够获取该干扰源影响范围内的众多通用接收机的位置丢失点信息和位置重获取点信息, 就能够建立关于干扰源位置的方程组,通过求解方程组,将能实现GNSS干扰的粗定位.
1.2 GNSS干扰定位算法
假设对于某区域内受干扰影响的接收机在一段时间里持续受到干扰,并且干扰源是固定的.如图1所示,在影响区域范围内,会有多条运动轨迹中发生位置信息丢失以及位置信息重获取,此图示意的运动轨迹为直线,在实际中运动轨迹是多样的.
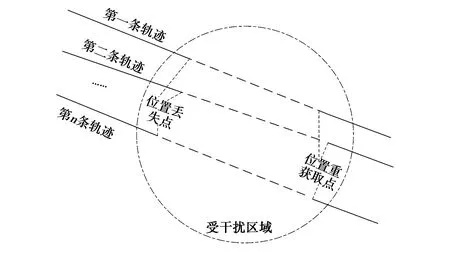
图1 受干扰影响轨迹示意图
造成GNSS接收机无法定位和重新定位的干扰功率是一定的,设受影响的第i个接收机由于干扰无法定位和重新定位的位置处对应的受影响的干扰功率分别为PLi和PRj、干扰源的功率为PJ、干扰源到中断点和重捕获点的功率损耗分别为LLi、LRi,则可得:
PJ-LLi=PLi,
(1)
PJ-LRi=PRi.
(2)
式(1)减去式(2)得:
PLi-PRi=LRi-LLi.
(3)
式中:LRi和LLi可基于电波传播分析得到,这两个参量分别可由干扰源和接收机中断点之间的距离、干扰源和重捕获之间的距离计算得到.
视距传播条件下,传播路线的基本传输损耗公式为
Lf=32.44+20lgd+20lgf,
(4)
式中:d为传输线路长度,单位为km;f为频率,单位为MHz.
如果在非视距传播条件时,需要采用其它的ITU传播损耗计算公式.本文的算法验证基于视距传播条件.
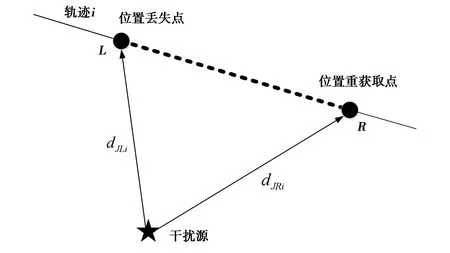
图2 第i条轨迹受影响示意
如图2所示,对于第i条受影响的轨迹,位置丢失点为L,位置重捕获点为R,干扰源为J,干扰源和位置丢失点以及位置获取点之间的距离分别为dJLi,dJRi,式(3)中LRi和LLi采用视距传播损耗公式进行计算,则可得:
(5)
在三维空间里,设干扰源的位置坐标为(xJ,yJ,zJ),位置丢失点的位置坐标为(xLj,yLi,zLi),位置重捕获点的位置坐标为(xRj,yRi,zRi),则由式(5)可得:
PLi-PRi=20lg
(6)
由于没有位置丢失点的位置信息,该点的位置信息用位置丢失前一时刻的位置信息代替.
PLi-PRi的值取为5 dB,代入式(6),式中的未知数仅为干扰源的位置,在同一个干扰源影响的范围内,如果能获取三条以上不同航线的位置丢失点以及位置重获取点,则可求得干扰源的位置.
对式(6)进行线性化及采用最小二乘法求解式(6)组成的方程组.
对式(6)进行线性化,得:
fk(xJ,yJ,zJ)=(xJ-xLk)2+(yJ-yLk)2+
xRk)2+(yJ-yRk)2+(zJ-
zRk)2].
(7)
通过寻找GNSS干扰源的初始位置(xJ,0,yJ,0,zJ,0)开始线性化,更新的干扰源坐标为
(8)
式中:ΔxJ1、ΔyJ1、ΔzJ1为增量.f(xJ,1,yJ,1,zJ,1)的泰勒展开式为
fk(xJ,1,yJ,1,zJ,1)=fk(xJ,0,yJ,0,zJ,0)+
(9)
经过这种变化后,方程(7)的线性化方程为
(10)
对于每一个有位置信息丢失和位置信息获取的接收机,都可以建立方程(10).当存在三个及三个以上这样的接收机信息时,可以求解出干扰源的位置.
对于方程(10)组成的方程组,采用最小二乘方法进行求解.
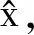
(11)
采用此方法可求得方程(10)的解ΔxJ1、ΔyJ1、ΔzJ1.将此解代入式(8),可求得干扰源的新位置,循环计算,直到ΔxJ1、ΔyJ1、ΔzJ1收敛到设定阈值为止.
2 算法仿真及性能分析
采用MATLAB作为仿真平台,通过计算干扰源定位误差来分析本文算法的GNSS干扰定位性能.假设仿真中加入的干扰源的位置为(xJR,yJR,zJR),采用算法定位的干扰源的位置为(xJC,yJC,zJC),则定位误差Perror按照以下公式计算:
Perror=
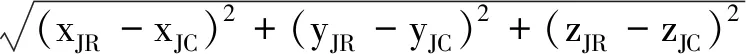
(12)
在仿真分析中,取干扰源的位置为(20 km,20 km,0 km),干扰源的功率为30 dBm(1 W),有效的可用于干扰源定位的运动轨迹为10条,且为三维空间的直线运动轨迹,引入的误差为1 dBm.假设干扰传播条件为视距传播,干扰源固定.视距传播条件、干扰源的功率为30 dBm时,计算得到的干扰影响距离为50 km,采用本文的GNSS干扰定位算法得到的结果如图3所示,计算得到的干扰源定位误差为152.424 9 m.因此本文的GNSS定位方法是可行的.
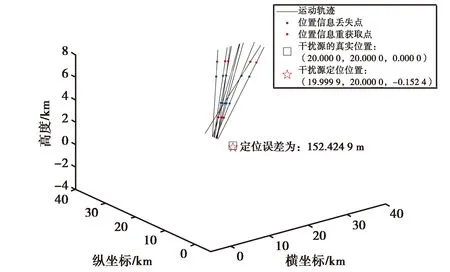
图3 仿真定位结果
下面分析干扰源的功率、有效的可用于干扰源定位的轨迹数量、引入的误差对GNSS干扰源定位结果的影响.
2.1 干扰源的功率对定位结果的影响
分析干扰源功率对GNSS干扰定位结果的影响时,保持其它因素不变,设置有效的可用于干扰源定位的轨迹数量为10条,引入的误差为1 dBm.当干扰源的功率分别为300 mW、500 mW,得到的定位结果分别如图4和图5所示,定位误差分别为46.183 2 m和76.750 2 m.
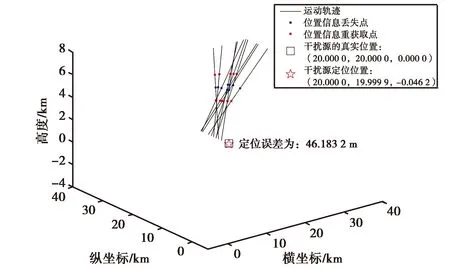
图4 干扰源功率为300 mW时的仿真定位结果
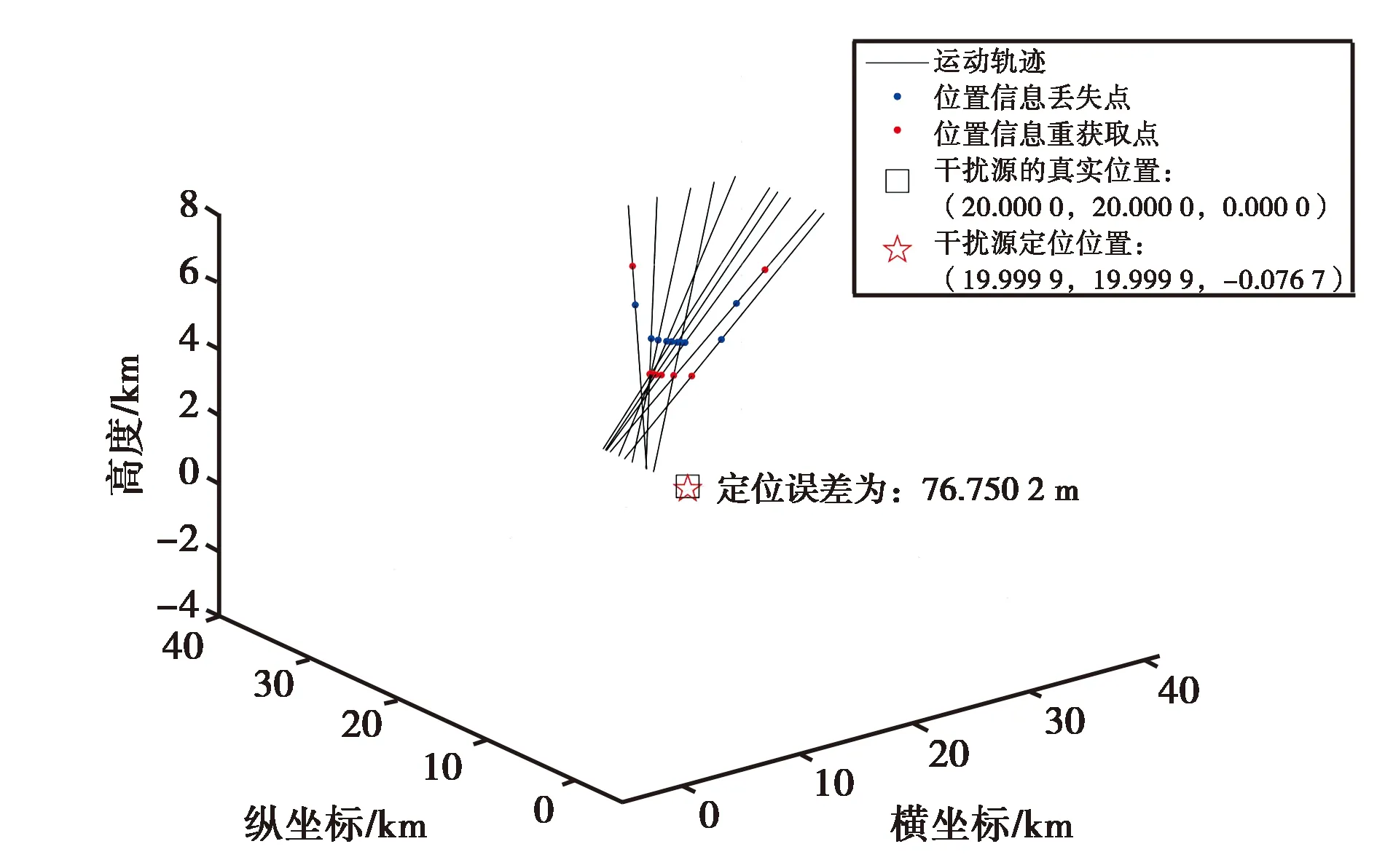
图5 干扰源功率为500 mW时的仿真定位结果
结合图3、4、5的仿真定位结果对比可以得出,当其它因素一定时,干扰源功率越小,本文定位算法得到的定位误差越小.
2.2 轨迹数量对定位结果的影响
分析有效的可用于干扰源定位的轨迹数量对GNSS干扰定位结果的影响时,保持其它因素不变,设置引入的误差为1 dBm,干扰源的功率为1 W,当轨迹数量取8条和15条时得到的定位结果分别如图6和图7所示,定位误差分别为152.419 7 m和152.388 6 m.
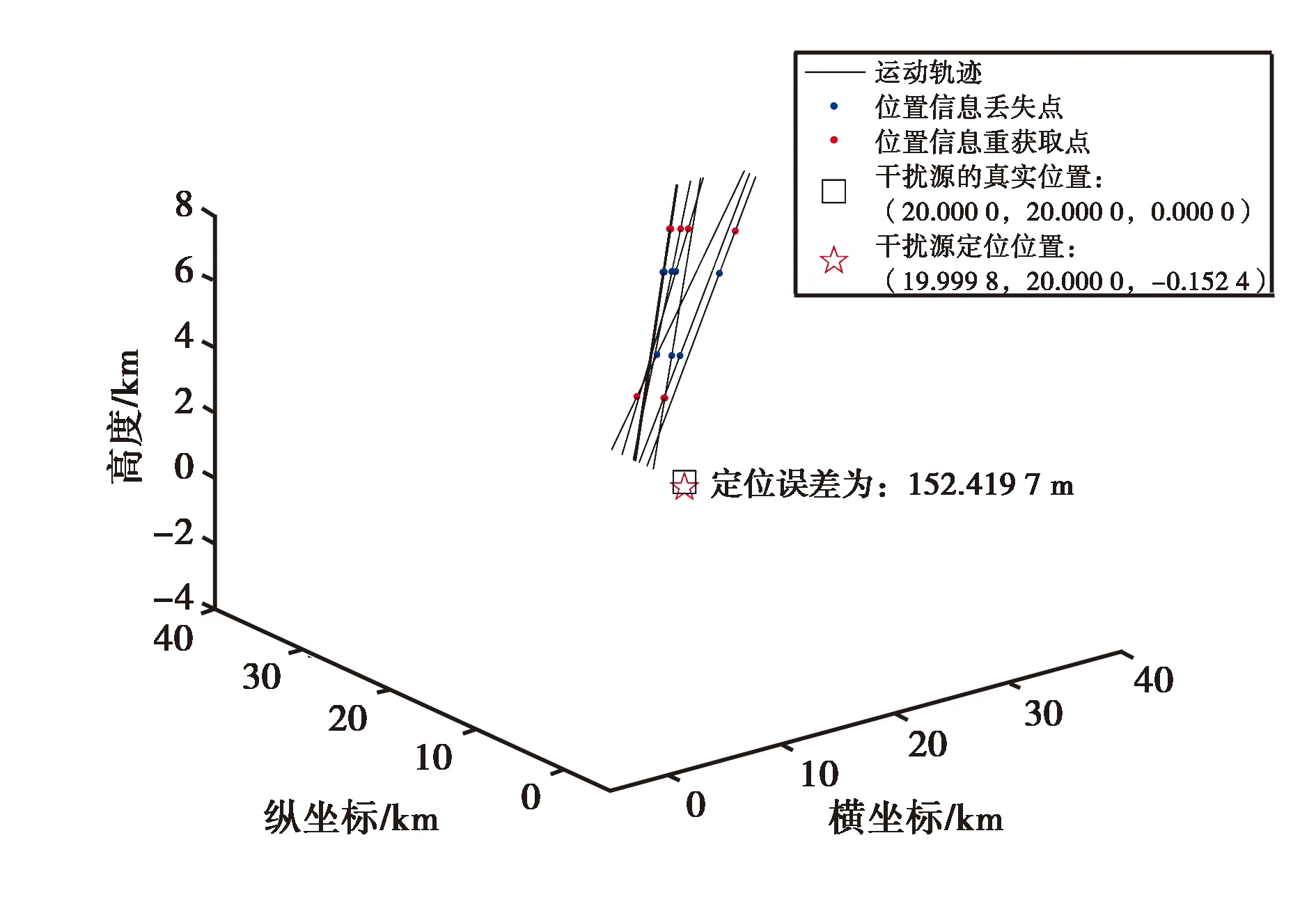
图6 轨迹数量为8条时的仿真定位结果
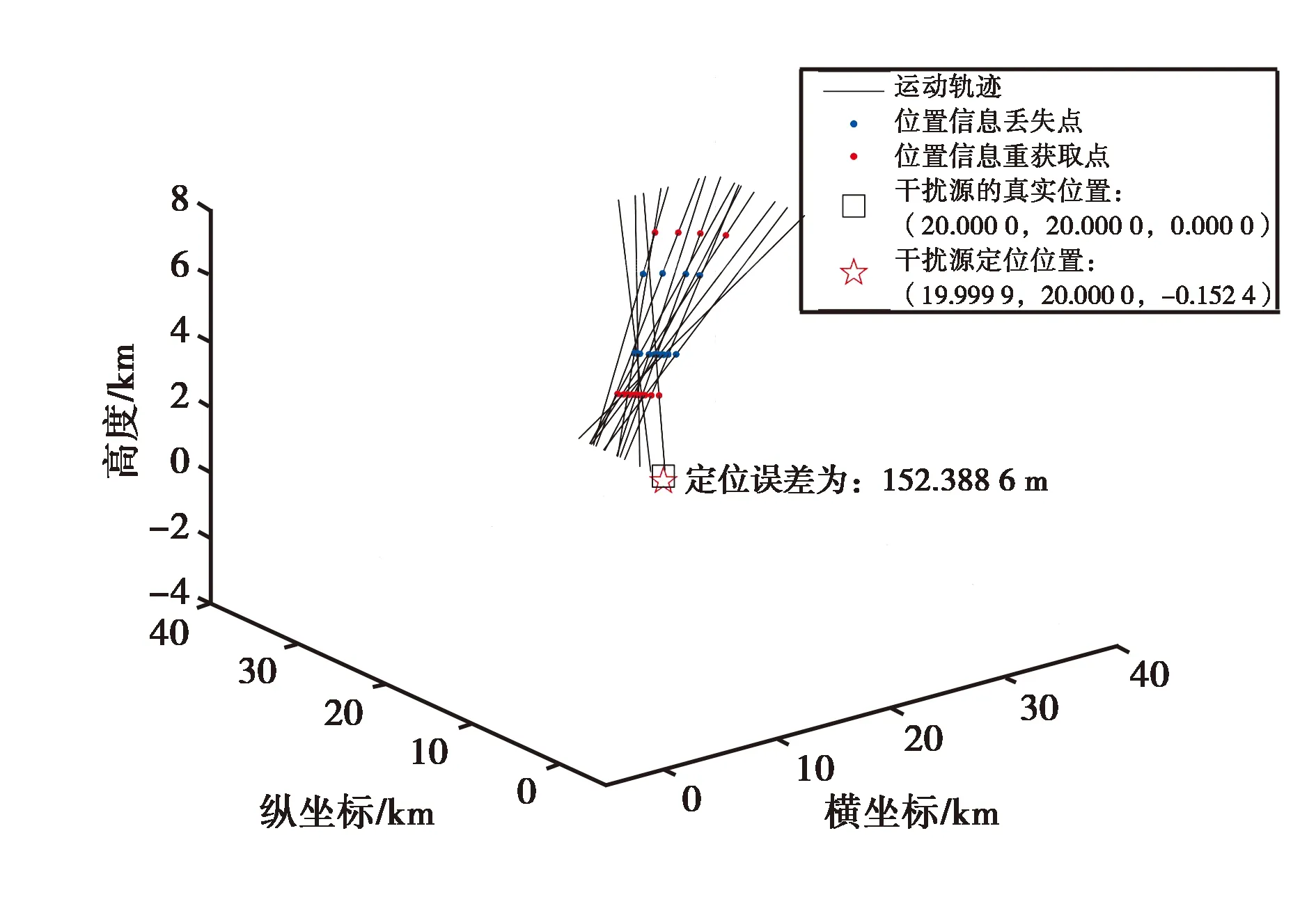
图7 轨迹数量为15条时的仿真定位结果
结合图3、6、7的仿真定位结果对比可以得出,当其它因素一定时,有效的可用于干扰源定位的轨迹数量对干扰源定位结果的影响不大.
2.3 引入误差对定位结果的影响
分析引入的误差对GNSS干扰定位结果的影响时,保持其它因素不变,干扰源的功率为1 W,轨迹数量10条,当误差分别为3 dBm和5 dBm时得到的定位结果分别如图8和图9所示,定位误差分别为239.570 5 m和370.864 8 m.
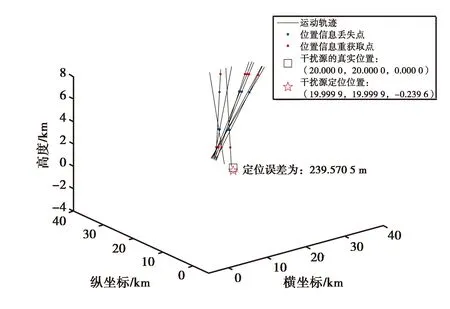
图8 引入误差为3 dBm时的仿真定位结果
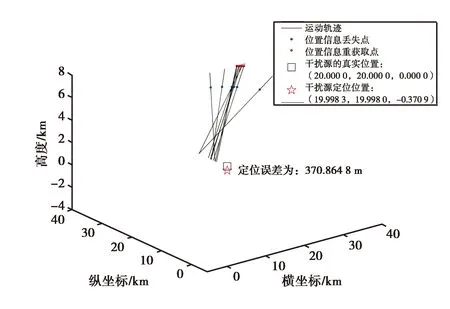
图9 引入误差为5 dBm时的仿真定位结果
3 结 论
通过数据仿真分析,本文研究的利用通用接收机在受到干扰后的位置丢失点和位置重捕获点的信息实现GNSS干扰源的定位算法是可行的.在影响范围为50 km时,定位的精度为几百米.当参与定位的运动轨迹数量足够时,具体的定位精度受干扰源的功率以及引入的误差影响.在其他因素一定时,干扰源的功率越小,定位误差越小;引入的误差越小,定位误差越小.

