确定飞机最大抖振设计载荷的长期极值估计方法

李 斌，张玉杰，杨智春

(西北工业大学 航空学院，西安 710072)

抖振是现代双垂尾战斗机［1］(大攻角机动引起旋涡破裂)和特种电子作战飞机(外加电线类凸起物引起气流分离)在服役过程中经常要遭遇的复杂动载荷环境，属于典型气弹响应问题。因此对于这类飞机在设计过程必须精细考虑其抖振载荷对结构安全的影响。在现代飞机结构设计中，振动严重部位的动态设计载荷的确定要求合理确定振动过程中的可能最大响应、并估计最大响应对应的最大内力载荷。尤其对于具有不确定特性的随机振动过程，如何根据有限的测试或计算样本数据，恰当地估计最大动态设计载荷，则显得更为重要。

飞机设计的工程实践中，在随机振动工况下，确定动态设计载荷的传统习惯方法是采用所谓的3σ法则，其中σ指振动响应的均方根值。该法则的数学内涵为，Gauss随机变量在(－3σ，3σ)区间外取值的概率为0.27%。但实际飞机设计中对限制载荷的定义是服役中预期的最大载荷［2］。很显然3σ法则确定的极值载荷一般是不满足限制载荷定义的。但是在飞机没有服役之前，缺乏安全使用寿命飞行数据的条件下，难以直接得到最大载荷峰值，只能根据有限的计算数据或风洞试验数据，采用预估方法进行估计可能出现的载荷最大值。目前在飞机设计过程，可供参考的一类确定动态载荷峰值的方法是根据指定的超越次数指标来截取极限载荷。如对突风载荷设计，Hoblit［3］推荐的限制设计超越次数是2×10－5次/飞行小时。这种基于设计超越次数指标的抖振载荷设计方法在F－22飞机完成试飞测试，获得大量抖振试飞数据后也得到了应用。文献［4］给出的确定极限载荷的可接受超越指标为全寿命周期内107次飞行发生一次，或超越概率为1×10－4。但这种方法应用的前提是必须先建立飞机全寿命周期的抖振载荷超越曲线，这对于设计阶段的抖振载荷预估确定来说难以满足。

确定设计阶段的抖振最大设计载荷，可以利用的数据有:缩比模型的风洞试验数据和抖振响应计算数据。这两种参考数据均只是有限长度，不可能覆盖全寿命周期。因此，有必要建立一种可靠的统计预测方法，利用短时间段内的响应数据，来预测飞机全服役时间内可能发生的最大抖振载荷。极值估计理论是解决这类问题的有效手段之一［5］，目前已经在土木结构的风工程研究领域得到较为广泛的应用［6］。本文结合某型飞机尾部结构的抖振风洞试验数据，运用次序统计和极值估计理论，基于极值I型分布和III型分布，分别应用线性的最小二乘估计和最大似然估计进行极值模型的参数估计，并根据预设极值重现期指标进行抖振响应数据的极值估计。此外，通过不同分析方法的对比，阐明了传统的3σ法则的局限性，并给出了应用极值估计理论确定动态设计载荷时的若干建议。

1 极值估计理论

用X1，X2，…，Xn代表n个独立的样本，x是任意样本Xi的最大绝对值，在大样本数目的条件下，Gumbel给出了x的三种渐近分布。这三种分布可以统一用广义极值分布函数表示:

式中，β=0称为极值Ⅰ型分布，实际是一种双参数分布函数;β＜0表示极值Ⅱ型分布;β＞0表示极值Ⅲ型分布。后两种都属于三参数分布函数，分布函数的尾部较长。参数α，β，v具有确定的物理含义。β称为形状参数，确定极值分布函数的形状;v为位置参数，表示最频繁发生的极值水平，对应分布密度函数的中心峰值位置;α为尺度参数，表示极值水平随对数时间变量的增长率;α/β则表示可能发生的极值。实际应用过程中，极值Ⅱ型或Ⅲ型分布的适用性由估计形状参数β决定。

在极值估计中，重现期是一个非常重要的概念，假定单个样本数据占据的物理时间长度为Δt，则重现期的数学表达式为:

式中，t称为对数减缩变量，t= －lnln［1/F(x)］。重现期tN的物理意义是观察到等于或大于x的极值所需的操作时间长度。1－F(x)表示超越概率。

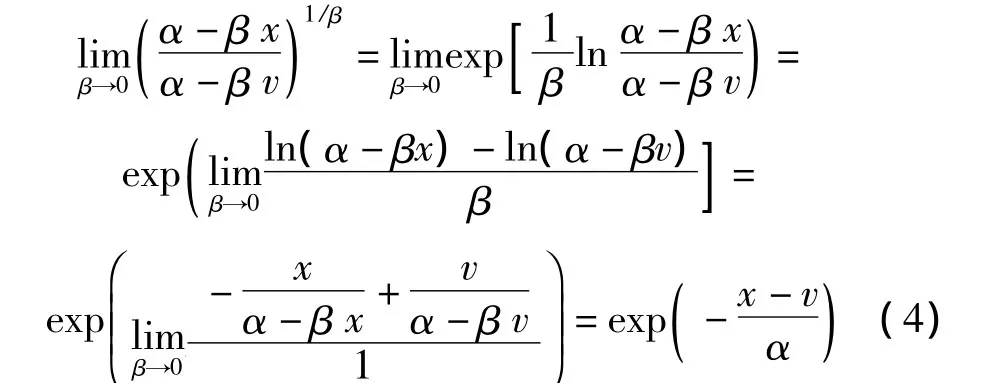
将式(4)代入式(1)可得I型分布函数的表达式为:

比较式(1)和式(5)，可以发现，Ⅰ型分布属于双参数分布，估计方便，计算简单，而且对取值无上下限要求。Ⅲ型分布属于三参数分布，可估计的数据类型较广，能够有效地弥补Ⅰ型分布的缺陷。

2 参数估计方法

2.1 基于经验分布假设的最小二乘估计法

对于Ⅰ型分布，x的总体分布函数如式(5)所示。引入变量:

则式(5)可化为:

将式(7)代入式(3)，推导出x－T关系式:

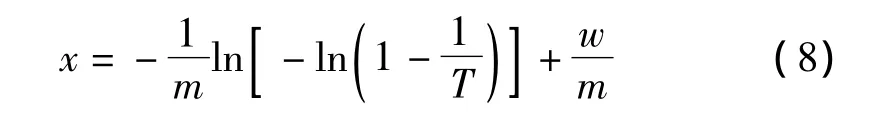
或x－t关系式:

对于Ⅲ型分布，x的总体分布函数如式(1)所示。引入变量:

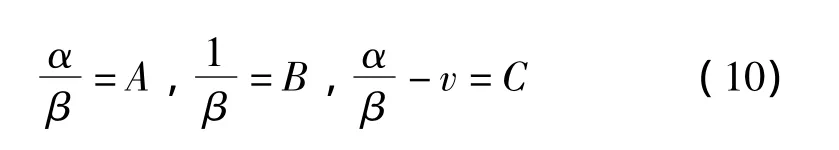
则式(1)可化为:

将式(11)代入式(3)推导出x－T关系式:

或x－t关系式:

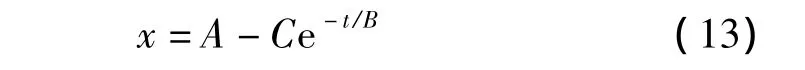
应用最小二乘法进行参数估计的一般步骤为:(1)将选定时间段内的数据分为n份，从每份中选取最大绝对值x;

(2)将这n个x值按从小到大顺序排列;

(3)引入经验分布函数，经过次序排列后的极值分布函数可以表示为:F(x)=i/n，或F(x)=i/(n+1)，i=1，2，…n。为避免F(x)=1时t无解的情况出现，一般取后者。引入t的定义，则t=－lnln［(n+1)/i］;

(4)对于Ⅰ型分布，考虑到式(9)，引入x关于t的线性表达式:x=at+b;对于Ⅲ型分布，考虑到式(13)，引入x关于t的指数表达式:x=DeEt+F;

(5)依据经验分布函数，对应每一个级别x，可以计算得到对应的t，将它们代入到步骤(4)的参数方程，可以建立a，b或D，E，F为未知量的矛盾方程组，然后求解该矛盾方程组的最小二乘解。其中求解D，E，F的具体做法是，令d=eEt，根据d和x相关系数最大的原则确定E。当E确定后，就可由线性最小二乘法拟合D和F，详细算法参考文献［7］;

(6)将 a，b或 D，E，F的估计值分别回代到式(6)、式(10)中，可得参数 α，β，v的估计值。

2.2 最大似然估计法

下面用最大似然估计法分别导出Ⅰ型分布和Ⅲ型分布参数的计算公式。

对于如式(7)所示的Ⅰ型分布函数，分布密度为:

似然函数为:

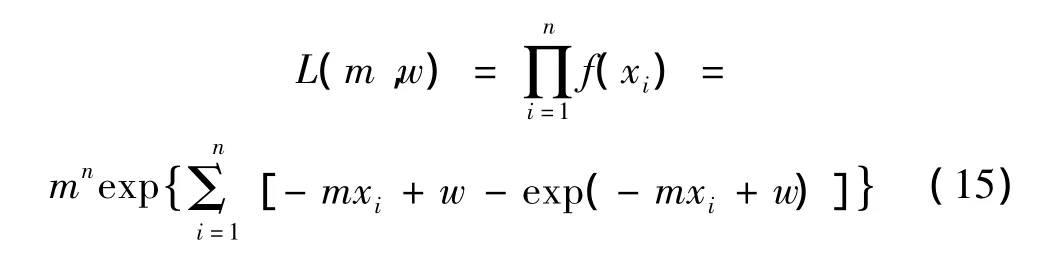
对式(15)两边取自然对数可得:

lnL(m，w)取极值的条件为:

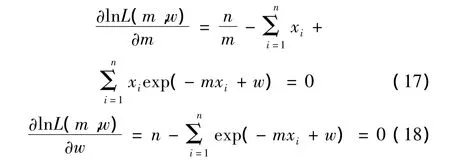
可以利用Gauss-Newton迭代法求解式(17)、(18)组合而成的以m，w为未知数的非线性方程组。本文具体计算时应用MATLAB自带的非线性求解函数“lsqnonlin”进行求解。

对于如式(11)所示的Ⅲ型分布函数，它的分布密度为:

似然函数为:

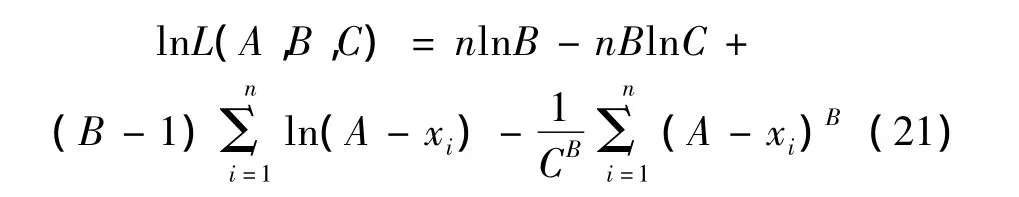
对式(20)两边取自然对数可得:

对 lnL(A，B，C)取极大值，得:

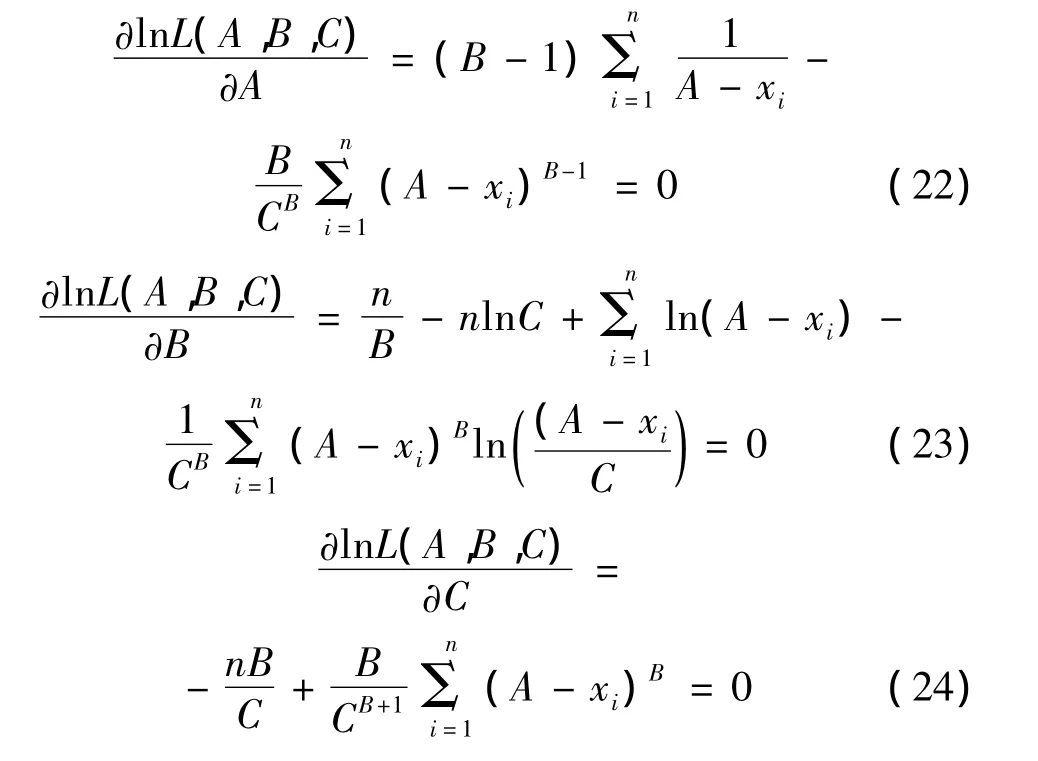
同样可以利用Gauss-Newton迭代法求解式(22)、式(23)、式(24)组合而成的以A，B，C为未知数的非线性方程组。对于Ⅲ型分布，初值的选取显著影响计算结果。参照文献［7］，A，B，C 初值分别取为 1.5xn，5，1.5xn－0.4，其中，xn为数量为 n 的极值样本中的最大值。

3 应用实例与分析

应用长期极值估计理论，可以建立振动响应极值大小与样本数量(即重现期)之间的关系。实际设计中则可以通过给定重现期来求取对应的设计极值。例如在土木工程结构的设计规范中，确定结构风载荷时通常定义“几十年”一遇的重现期。

对于飞机抖振设计载荷确定来说，重现期的确定可以遵循如图1所示的流程框图来预设。首先影响确定影响抖振响应烈度的敏感参数，并用敏感参数来进行典型状态的划分。然后按照飞机使用习惯，确定飞机的典型任务剖面。要求每个典型任务剖面内，每飞行小时各典型状态的可能累积发生时间相对稳定。最后根据飞机的全寿命周期使用统计情况，将整个飞行寿命周期内的典型状态可能发生的时间累加起来则可以得到对应的“典型状态”的设计重现期。依据该重现期，则可进行设计载荷极值的估计。

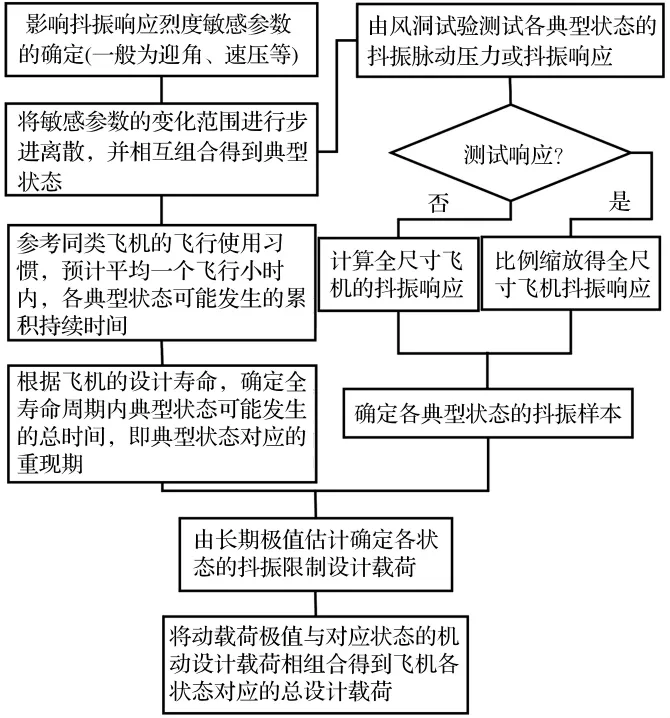
图1 抖振设计载荷确定框图Fig.1 Flow chart to determine buffet design load

下面以某型飞机尾部结构的抖振响应风洞试验测试数据为例进行极值估计方法的实例讨论。如图2所示为通过风洞试验获得的某型飞机尾部结构的典型加速度振动响应数据，数据采样频率为2 048 Hz，采样时间24 s。为了有利于统计模型的参数估计，对原始数据幅值进行了无量纲规范化处理，即将测试数据统一处理到±0.8的变化范围内，Ca=对该数据进行正态分布检验，统计和拟合得到的概率密度曲线和分布曲线分别如图3所示，可见响应数据符合正态分布假设，响应属平稳随机过程。

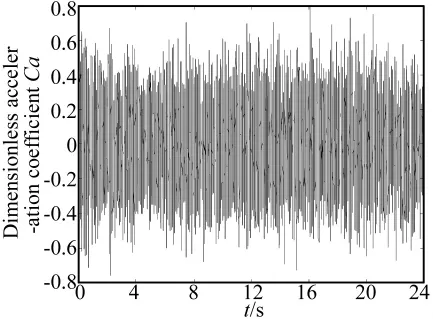
图2 测试的抖振响应样本Fig.2 Sample of measured buffet response data

图3 抖振数据正态分布检验Fig.3 Probability distribution check of buffet data

3.1 关于极值模型和估计方法的讨论

为了检验极值估计模型和估计方法的适用性，以图2所示的24 s长度的数据作为数据总体，根据前文对数据的规范化处理方法，可知其理想极值为0.8。以每128个时域测试数据作为一个样本，则每个子样本对应的时间长度Δt=0.062 5 s。提取各个子样本内的极值(绝对值)，进行极值分布参数估计分析。应用第2节所述的最小二乘法和最大似然法分别进行极值Ⅰ型分布和Ⅲ型分布的参数估计，结果如表1和图4所示。

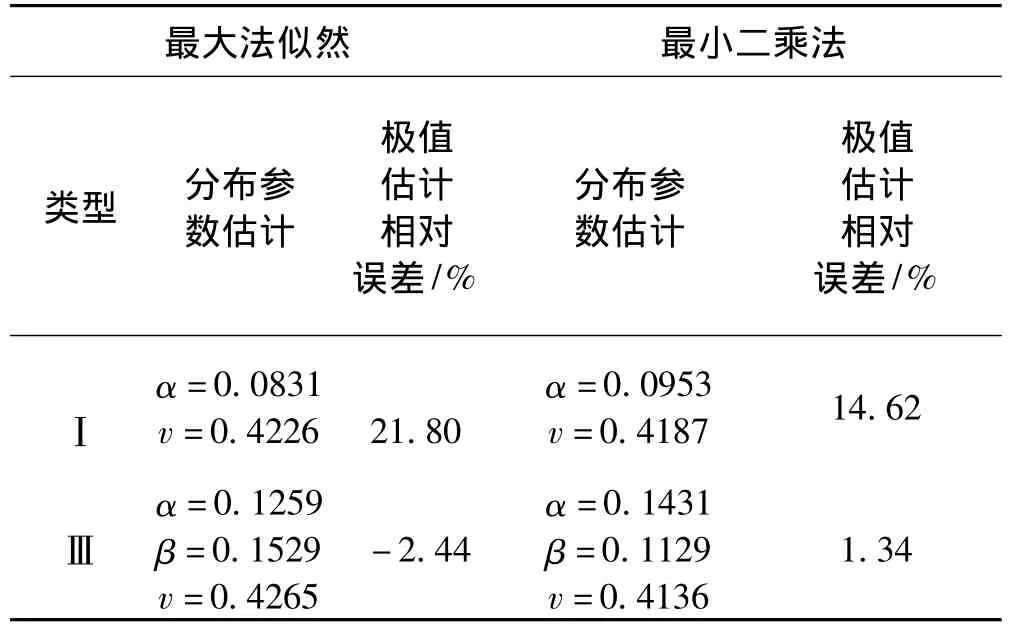
表1 Ⅰ型和Ⅲ型分布模型对比Tab.1 Comparison betweenⅠ andⅢ distribution model

观察表1可以发现，无论采用最小二乘法还是最大似然估计法，Ⅰ型分布估计出来的极值偏差都比实际值大14%以上，过于保守。Ⅲ型分布估计得到的最大抖振载荷更接近实际值，图4中两种模型得到的极值估计曲线与试验数据统计曲线的对比也说明了这一点，Ⅰ型分布估计在初始阶段与实际统计曲线吻合较好，但随着对数减缩时间变量的增长，曲线后段的偏离越来越大。导致这种现象的主要原因是双参数模型较难描述长尾分布。如图5所示为超越概率分布曲线，Ⅲ型分布模型明显改善了曲线后段的描述精度，拟合后的总体趋势曲线与实际统计数据之间的吻合性非常好。

图4 Ⅰ型和Ⅲ型分布估计值和试验值的对比Fig.4 Comparison of measured and predicted extreme value using distributionⅠandⅢ

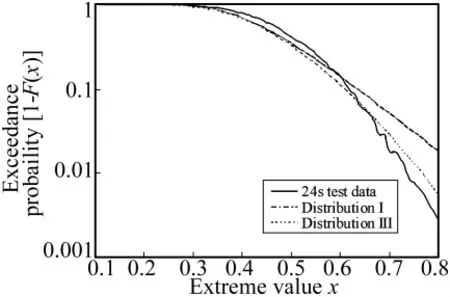
图5 超越概率分布曲线对比Fig.5 Comparison of measured and predicted exceedance probability using distributionⅠandⅢ

表2进一步采用抖振风洞试验中获得的10组不同的24 s长度的测试数据，基于Ⅲ型分布，分别应用最小二乘法和最大似然估计法进行了载荷极值估计，估计结果如表2所示。对比分析各组数据表明，应用最小二乘法估计出来的最大抖振响应值较试验值略低，属于偏冒险的情况;应用最大似然估计法，估计出的最大抖振响应值较试验值略高，属于偏保守的设计。两种参数估计算法得到极值估计精度都在±5%以内，适于工程应用，且整体来说最大似然估计法的精度要略高于最小二乘法。

表2 两种参数估计方法的结果比较Tab.2 Comparison between results obtained by two parameter estimation methods

3.2 关于测试数据样本量的讨论

由于在实际的动态信号测量过程中，稳定状态持续时间和数据采集时间总是有限的。尤其对于飞机的飞行测试试验，飞行参数及姿态持续稳定的时间非常短。本节将从进行长期极值有效估计的角度，讨论测试数据样本量对估计精度的影响，以便确定合理的采样长度。

以图2所示24 s秒长度的测试数据为例，分别截取时间长度为 0.5 s，1 s，1.5 s，2 s，2.5 s，5 s，24 s 的数据，按Ⅲ型分布模型应用最大似然估计法进行参数估计，并进行极值预测。同时对不同长度的样本数据求相应的均方根值，并按照传统的3σ法则估计设计载荷，以便对比。

计算结果如表3所示，应用2 s长数据，32个统计样本，进行参数估计，即可较为准确的识别分布模型参数，对应24 s重现期估计得到的极值与实际极值之间的误差小于5%。并且由识别参数随样本数量变化趋势可见，参数识别结果随样本数量的增加趋于稳定。而简单由3σ法估计的设计载荷明显低于24 s内的极值载荷。如果采用4σ，则基本逼近24s内的极值载荷。更进一步，由不同时间长度数据得到的均方根值变化可知，对于本文所分析的平稳过程数据，仅0.5 s数据即可准确获得振动响应的基本统计特征。这说明平稳过程的数据样本长度对均方根值计算的影响不大。但是如要根据均方根值来估计长期极值，则需要借用合理的判据来确定σ的放大倍数，而本文所提的极值估计法恰好可以用来实现合理倍数的估计。

3.3 长期极值估计

假定图2所示的数据表示飞机在以下飞行条件下的典型抖振响应数据。3 000 m高度巡航，马赫数Ma=0.6，机翼迎角 αw=4°，方向舵偏角 15°(尾部结构抖振响应对方向舵偏角比较敏感，所以选用该参数进行状态划分)。以该数据段作为一个划分后的典型状态代表。

设每个飞行小时内，该状态的累计发生时间为300 s，飞机的设计寿命为6 000飞行小时。据此可以推断在飞机的整个寿命周期内该状态可能发生的总持续时间为 1 800 000 s。取 Δt=0.062 5 s，按照式(2)式(3)设定tN=1 800 000 s，可求得设计超越概率为:

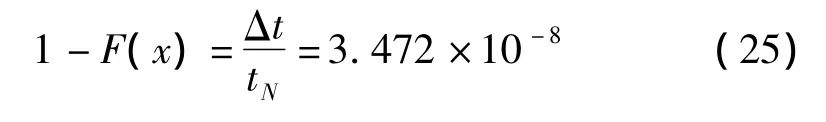
将式(25)代入到式(1)，并且根据事先得到的估计参数，可求得对应的设计极值为1.145。

4 结论

本文利用次序统计和长期极值估计理论，结合某型飞机尾部结构的抖振风洞试验数据，应用极值Ⅰ型分布和Ⅲ型分布参数进行了抖振响应极值估计研究，相关结论如下:

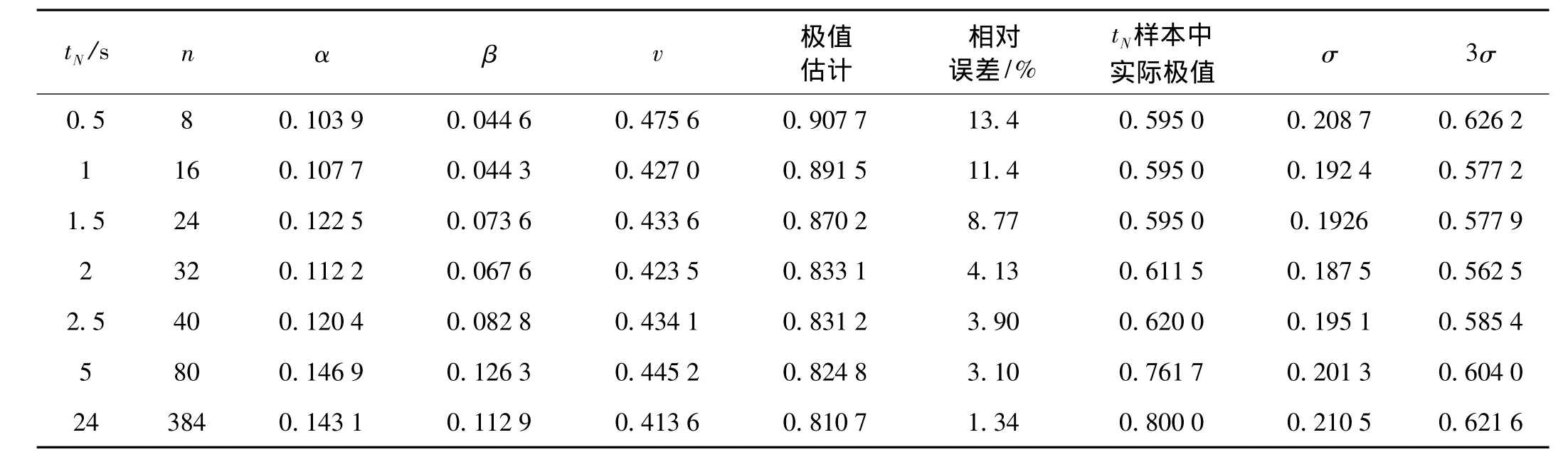
表3 样本长度对估计精度的影响(Ⅲ型分布，最大似然法估计)Tab.3 Prediction accuracy varies with tN(distribution Ⅲ ，maximum likelihood method)

(1)对于平稳随机过程，Ⅰ型分布模型的极值估计精度明显没有用Ⅲ型分布模型估计的精度高。原因在于Ⅰ型分布为双参数模型，难以准确描述长尾分布，三参数的Ⅲ型分布模型明显改善了超越概率曲线的后段描述精度。

(2)在数据样本足够的情况下，最小二乘法估计法和最大似然估计法都可以较为准确地实现分布参数估计，极值估计精度在±5%范围内，适于工程应用。但总体趋势上最大似然估计法的估计精度略高于最小二乘法。

(3)通过数据对比分析可知，对平稳随机振动过程，传统的3σ设计原则不能满足飞机设计中对确定限制载荷的要求，根据3σ设计原则确定的限制载荷将偏危险。长期极值估计法更加符合飞机限制载荷的确定要求，值得在工程设计中进行推广应用。

(4)要实现飞机抖振载荷准确有效的极值估计，对采集样本数量有一定的基本要求。该基本要求可以确定最小响应采集时间，该指标对于振动响应测试方案和数据处理方法的制定有一定的指导性意义。

［1］Lee B H K.Vertical tail buffeting of fighter aircraft［J］.Progress in Aerospace Sciences，2000，36:193 －279.

［2］中国民用航空管理局.中国民用航空规章第25部:运输类飞机适航标准(CCAR－25－R4)［S］.北京:中国民用航空局，2011.

［3］HoblitF M. GustLoads on Aircraft:Concepts and Applications［M］.USA:AIAA，1988.

［4］Patel S R，Black C L，Anderson W D.F/A－22 Vertical tail buffet strength certification［C］.46th AIAA/ASME/ASCE/AHS/ASC Structures，StructuralDynamics ＆ Materials Conference，Austin，Texas，2005.

［5］Lee B H K.Statistical analysis of wing/fin buffeting response［J］.Progress in Aerospace Sciences，2002，38:305 －345.

［6］段忠东，欧进萍，周道武.极值风速的最优概率模型［J］.土木工程学报，2002，35(5):11 －16.DUAN Zhong-dong，OU Jin-ping，ZHOU Dao-wu.The Optimal Probabilistic Distribution for Extreme Wind Speed［J］.Journal of China Civil Engineering，2002，35(5):11 －16.

［7］赵 伟，杨永增，于卫东，等.长期极值统计理论及其在海洋环境参数统计分析中的应用［J］.海洋科学进展，2003.24(4):471－476.ZHAO Wei，YANG Yong-zeng，YU Wei-dong，et al.Longterm extreme value statistics theory and its application to the marine environmental parameter statistics and analysis［J］.Advances in Marine Science，2003，24(4):471 －476.