传感器冗余的磁悬浮轴承转子系统研究

肖鹏飞，谢振宇，徐 欣，龙亚文

(南京航空航天大学 机电学院，南京 210016)

磁悬浮轴承是利用电磁铁产生可控电磁力将转子无接触地悬浮的一种新型轴承，与传统轴承相比，磁悬浮轴承具有无磨损、无污染、无需润滑以及刚度阻尼可调等优点［1］。但是，磁悬浮轴承系统包含传感器、控制器和功率放大器等，远比传统轴承复杂，因此如何提高磁悬浮轴承系统的可靠性是目前研究的热点。

在众多提高系统可靠性方法中，对系统的易损环节进行冗余设计是提高磁悬浮轴承可靠性的有效途径。然而，作为系统最重要的环节之一的传感器，其探头被安装在转子附近，经常受到转子运行时带来的振动和高速气流的影响，最容易损坏，所以对传感器采用冗余设计成为提高系统可靠性的主要方法之一。

目前，国内外已经有许多学者对传感器冗余设计进行了研究。例如，Younggyu等［2］采用了冗余检测线圈的电感式位移传感器来检测转子的位移，以提高系统的可靠性。Kim等［3］通过测量磁轴承力和转子位移两种方式得到位置冗余信号，提高了传感器检测精度和系统的可靠性。周祖德等［4］提出一种以多值逻辑代数为指导的传感器冗余故障诊断技术，详细分析了冗余传感器的故障诊断过程。崔东辉等［5］采用了自适应滤波和DFT识别两种算法对冗余传感器进行了故障识别研究。

传感器冗余设计分为径向传感器冗余(传感器差动布置)和轴向传感器冗余两种形式。采用轴向传感器冗余设计不仅能提高系统的可靠性，同时还能够减少传感器测量点和轴承施力点不一致的问题带给系统的影响，以提高系统的测量精度。因此，本文建立了轴向传感器冗余的磁悬浮轴承转子系统，利用ADAMS和MATLAB软件对系统进行建模和联合仿真，结合设计好的控制策略和故障诊断方法建立了复杂的控制系统，通过模拟试验研究了系统在运行过程中传感器发生故障时的静态和动态特性。

1 磁悬浮轴承转子系统

1.1 系统结构

图1为系统机械结构平面图。其中1，11为轴向传感器，2，4和8，10分别为两对轴向冗余的径向传感器，5为轴向磁轴承，3，9为左、右径向磁轴承，6为内置高频电机，7为实心转子。

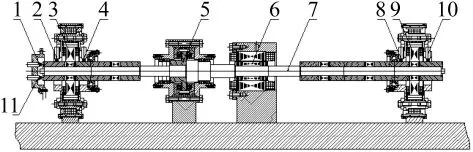
图1 系统机械结构图Fig.1 Mechanical structure of system

转子的振动信号可由径向磁轴承两侧和转子一端的电涡流传感器实时获得［6］。由于机械结构所限，传感器无法安装到磁轴承施力点处，因此存在传感器测量点和轴承施力点不一致的问题。为了减小该问题对动态性能的影响，系统分别将各径向磁轴承两端传感器以及转子左端两个轴向传感器输出的平均值作为转子的振动信号。

本文仅选取左径向磁轴承Y方向(第1自由度)的2#和4#传感器作为研究对象，其余各自由度与此相同。在系统正常工作时，2#和4#传感器输出的平均值作为第1自由度转子的振动信号被送入控制系统。当2#和4#传感器中的任意一个发生故障时，系统会及时诊断并立即切断该故障传感器信号，将剩下的传感器信号作为第1自由度转子的振动信号送入控制系统以使系统继续正常工作。

1.2 系统工作原理

图2为单自由度磁悬浮轴承系统工作原理图。

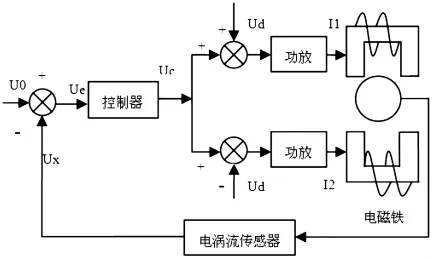
图2 单自由度磁悬浮轴承系统原理图Fig.2 Principle of AMB

转子在悬浮或旋转时由于外载荷和干扰而产生振动，电涡流传感器检测转子的位置，将位置信号与设定值(本系统为2.5V)进行比较并将差值输入到控制器中，经控制器计算后输出合适的控制电压并由功率放大器转化为控制电流输入到电磁铁线圈来改变电磁力的大小，使转子回到设定位置［7］。

2 系统建模与联合仿真

2.1 仿真模型

由于UG拥有强大的三维建模能力并且能够与ADAMS之间进行良好的数据交换，因此本文选用UG软件来建立磁悬浮轴承系统的机械模型，然后将该模型导入到ADAMS中。根据实际系统中各部分的材料特性在ADAMS环境下设置该模型各组件的材料属性、质量信息、转动惯量以及构件间的约束，同时在高频电机和转子之间添加一个速度驱动，其驱动函数为:

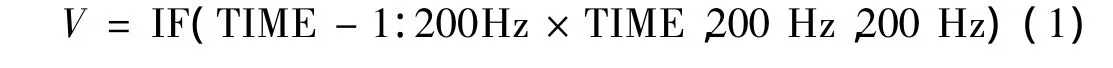
为了建立ADAMS与MATLAB之间的数据交换接口，在模型上创建了10个状态变量，其中5个输入变量(current1-current5)为电流、5个输出变量(distance1-distance5)为转子的位移，ADAMS与MATLAB之间的数据交换过程如图3所示［8］。

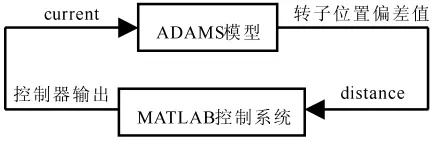
图3 ADAMS与MATLAB的数据交换过程Fig.3 Process of data interchanges between ADAMS and MATLAB

通过在轴承的定子和转子之间添加可控力约束来模拟磁场力，其中实际系统中电磁力的表达式为:

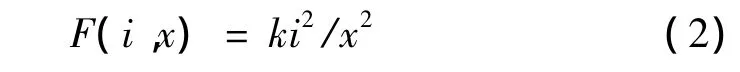
由于转子一般都在平衡位置附近作微小振动，因此电磁力可以通过泰勒公式线性化为:

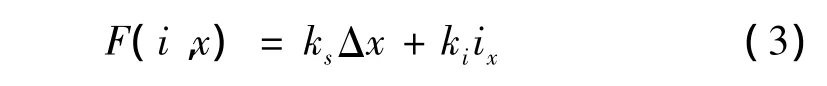
式中:ks，ki为位移刚度系数和电流刚度系数。根据设计参数，径向和轴向磁轴承位移刚度系数和电流刚度系数分别为:

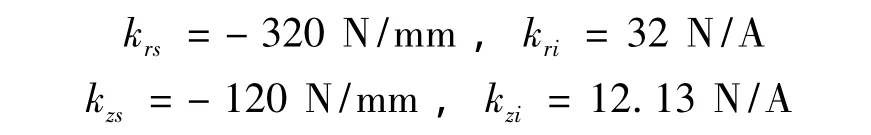
与磁场力等效的可控约束力表达式为:

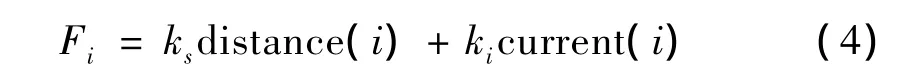
图4为磁悬浮轴承转子系统五自由度仿真模型。

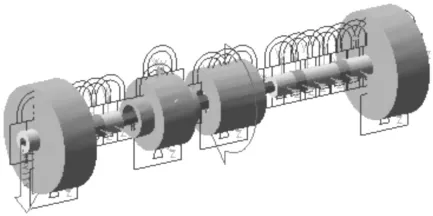
图4 系统五自由度仿真模型Fig.4 5 － DOF simulation model of system

2.2 控制策略

本文共设计了两种控制算法:不完全微分PID控制和模糊 PID 控制［9］。

不完全微分PID控制算法的传递函数为:

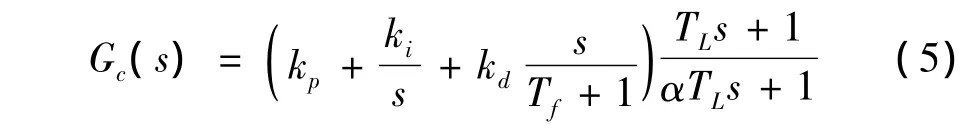
式中，kp为比例系数，ki为积分系数，kd为微分系数，Tf为一阶低通滤波器系数，TL为校正环节的时间常数。

根据传递函数(5)和初设的控制参数便可以在MATLAB/Simulink模块中建立控制器框图，然后通过调试找到最优控制参数即可用于联合仿真。

模糊PID控制策略设计过程中，最重要的是模糊规则的制定以及量化因子的取得。

本系统中，模糊控制器的输入变量分别为误差信号e(t)和误差变化率ec(t)，其表达式为:

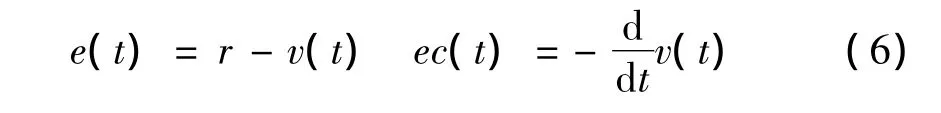
式中，r为参考信号，v(t)为传感器输入信号。制定模糊规则的具体过程为:当误差信号e较大时，并且误差变化率ec也向同一方向增大，为了使转子能够快速回到平衡位置，需要反方向的一个大的控制输出。同样，当e较大，但是ec反方向增大时，需要一个较小的控制力使转子回到平衡位置。利用以上类似的分析方法可以得到初步的模糊逻辑控制规则，在此基础上，通过分析和试验对其进行适当调整，得到最终合适的模糊逻辑控制规则Δkp，见表1。

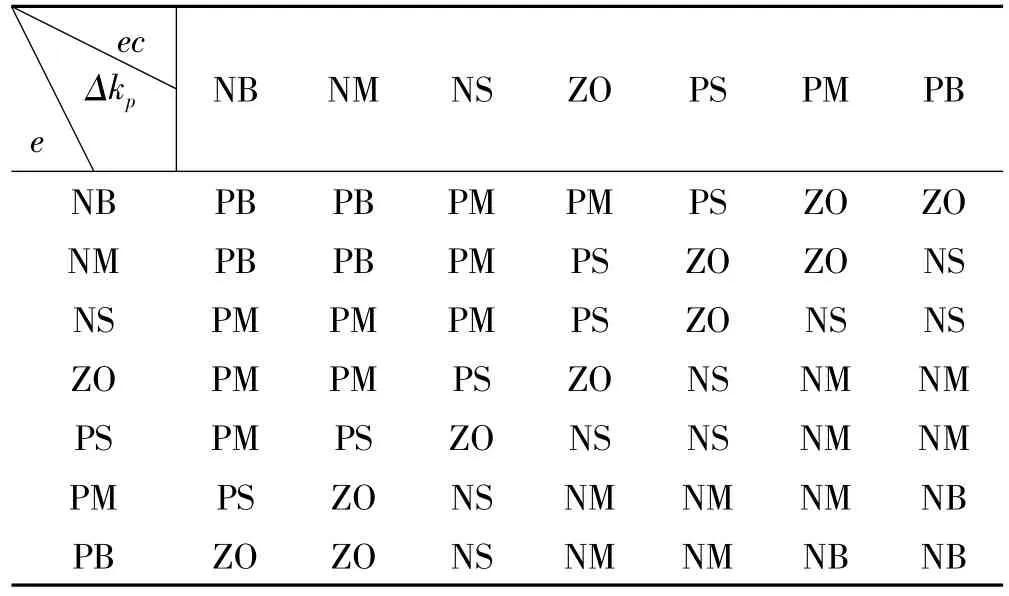
表1 模糊规则表Tab.1 rules of fuzzy control

其它两种控制参数的模糊规则表，在此不再给出。根据上述控制策略和各模块传递函数［10］，建立的五自由度模糊PID控制算法框图如图5所示。

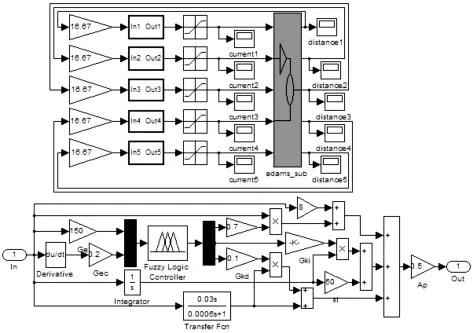
图5 模糊PID控制算法框图Fig.5 Control algorithm of fuzzy-PID

2.3 仿真计算

建立好仿真模型后，再指定输入输出变量，导出控制参数，建立好与MATLAB进行数据交换的接口，然后运用Simulink模块制定控制算法［11］。

建立好控制策略后，可设置仿真参数。根据实际需要设置仿真时间为0.5 s，通信周期为0.001 s，仿真模式为continuous，动画模式为interactive，同时采用变步长龙格－库塔法数值积分函数ode45进行数值积分。设置好仿真参数后即可对系统进行联合仿真［12］。

2.4 仿真结果

通过对联合仿真结果的优化，不完全微分PID控制参数为:kp=2，ki=10，kd=2，Tf=0.06。模糊 PID参数为 Ge=150，Gec=0.2，Gkp=0.7，Gki=0.2，Gkd=0.1，ki=10，kd=0.03，kp=8，Tf=0.000 6。

在上述控制参数下，转子在Y方向上的起浮过程如图6所示。

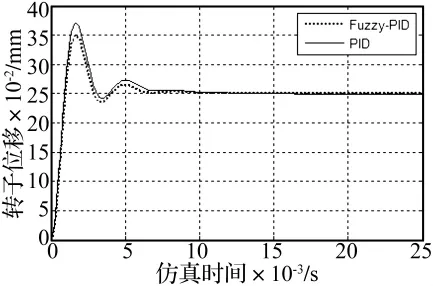
图6 转子Y方向上起浮曲线Fig.6 Vibration of rotor at Y direction

从图6可以看出，在两种控制策略下，转子均能够从磁悬浮轴承的最低位置起浮到轴承的设定位置并保持稳定;另外，在模糊PID控制下转子的超调量要略小于不完全微分PID控制，但是两者的调整时间基本相同，约为 0.007s。

选用上述两种控制策略和调整后的最优控制参数开始转子的仿真旋转试验。仿真驱动设置为:

式中t为仿真时间。转子开始从静止逐渐加速到12 000 r/min，当仿真时间为 0.3 s(9 000 r/min)时改变传感器输出，得到的转子振动曲线如图7所示。

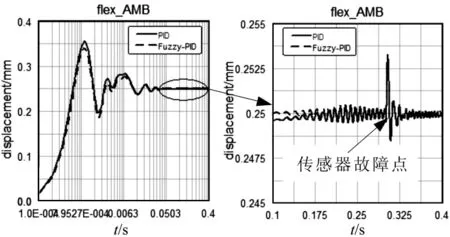
图7 升速过程的转子振动曲线Fig.7 Vibration of rotor in the Process of Acceleration

从图7可以看出，在转子起浮阶段，模糊PID控制下转子的超调量要比不完全微分PID控制时略少，但二者的响应速度和调整时间基本相同;在转子稳定运行时，不完全微分PID的静态精度要比模糊PID稍低。这说明模糊PID的控制效果要稍优于不完全微分PID。另外，在传感器位置发生改变时，转子出现了较小幅值的跳变，但在随后很短时间内转子又回到了平衡状态，这说明了在转子运行过程中改变传感器位置不会带来转子大幅度的振动或瞬间失稳。

当模拟转子在12 000 r/min恒定转速下运转时，在仿真的前0.85 s内，第1自由度的信号是由2#和4#传感器输出平均提供，在0.85 s时刻切断4#传感器的输出，其后第1自由度信号仅由2#传感器来提供，在改变传感器输出瞬间，在2#传感器位置处转子的振动曲线如图8所示。

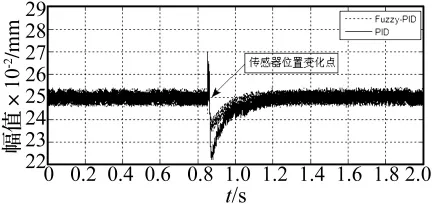
图8 12 000 r/min下转子振动曲线Fig.8 Vibration of rotor at 12 000 r/min

由图8可以看出，在12 000 r/min改变传感器输出时转子振动发生了较小的跳变，在其后0.2 s内转子又恢复到平稳状态，说明在该转速下改变传感器输出时没有造成转子大的振动跳变或者出现失稳;另外，采用不完全微分PID控制时转子的跳变量要比采用模糊PID控制时大，并且其恢复到平稳状态所用的时间也比后者长。另外，需要说明的是在低于12 000 r/min的其它各转速下恒定运行时，改变传感器输出所得到的仿真结果与图8类似，在此不再赘述。

3 传感器故障诊断方法和实现

在本系统中的传感器主要有两大类故障形式，分别为非完全型故障和完全型故障。其中非完全型故障主要包括:漂移偏差故障和固定偏差故障，主要是由偏置电流或偏置电压以及工作传感器发生温漂造成;而完全型故障主要包括:开路故障和短路故障，主要是由于传感器信号线的断路以及传感器硬件电路中芯片管脚未连接上或信号线短接造成的。

在本系统中，由于非完全型故障的诊断过程比较复杂，因此采用了基于BP神经网络的传感器故障诊断方法来实现故障传感器的准确判断。而完全型故障中的开路故障和短路故障造成传感器输出信号分别为5 V和0V，因此本文采用连续采样和信号比较的方式来判别故障传感器。图9为基于神经网络的传感器故障诊断原理图。

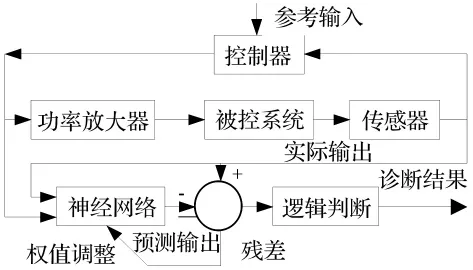
图9 基于神经网络的传感器故障诊断原理图Fig.9 Principle of fault diagnosis based on neural network

基于神经网络的传感器故障诊断过程为:假设在试验开始的一段时间里传感器未发生故障，此时神经网络根据转子信号进行网络训练，待训练达到设定的精度后，停止训练并开始传感器输出预测和诊断。在系统运行过程中，如果传感器的实际输出和神经网络的预测输出的残差值小于设定的阈值，认定传感器未发生故障，并根据此残差值调整神经网络各层权值;如果残差值大于设定的阈值，则判定该传感器发生故障，此时将另一个正常传感器的信号作为该路信号进行后续算法处理。

完全型故障判断过程为:控制器将2#和4#传感器输出的差值与设定阈值作比较，若此差值大于设定阈值，说明2#和4#传感器中有一个已经发生故障，进一步对比2#和4#传感器当前时刻信号与各自前一时刻的信号可确定失效传感器，此时失效传感器的信号不再采用，而只对另一传感器的输出进行算法处理;若2#和4#传感器的差值小于设定阈值，说明两个传感器均正常工作，此时控制器对2#和4#传感器输出平均值进行算法处理。传感器失效判别的具体流程如图10所示。

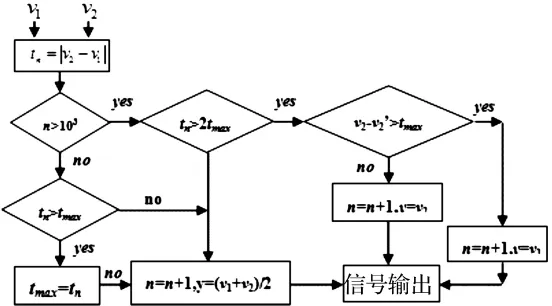
图10 传感器失效判断框图Fig.10 Fail judgment of sensors

4 系统试验

4.1 静态悬浮试验

当转子静态悬浮时，通过人为切断某一传感器信号线的方式来模拟该传感器失效。图11为在某一时刻人为切断4#传感器信号线时，4#传感器输出和2#传感器输出的变化。

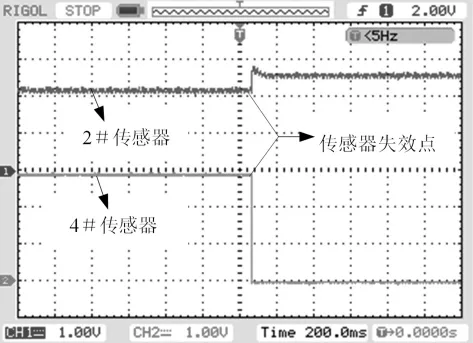
图11 静态悬浮时传感器输出Fig.11 Sensor output when the rotor is suspended

由图11可以看出，在切断4#传感器前，转子悬浮在设定位置，由于加工和安装误差，2#传感器输出为2.1 V，4#传感器输出为2.9 V，两者平均电压为2.5 V，这说明控制器以2#和4#传感器输出平均值作为处理对象;在4#传感器切断瞬间，4#传感器输出迅速变成0，此时2#传感器输出从切断前的2.1 V产生一个小的跳变，在随后0.1 s内变成了2.5 V，这说明转子第1自由度位置信号只由2#传感器提供，转子重新达到稳定悬浮状态。

4.2 高速旋转试验

分别采用模糊PID控制和不完全微分PID控制使转子稳定悬浮，并由内置高频电机带动转子高速旋转。在系统正常运行的某一时刻，利用信号发生器在目标传感器上添加一个漂移偏差信号，以模拟该传感器发生非完全型故障，然后对获得的数据进行故障诊断，并观测和比较诊断后的系统实际输出和网络预测输出以及它们之间的误差值。图12为传感器发生漂移偏差故障时实际输出和预测输出曲线。

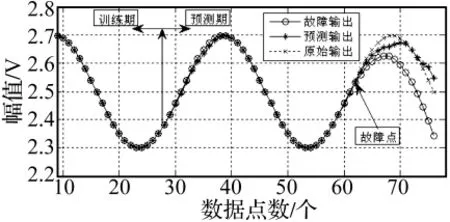
图12 传感器的实际输出和预测输出Fig.12 Real output and predict output of sensor

从图12可以看出，在传感器发生故障以前传感器的实际输出和神经网络的预测输出非常接近，说明该神经网络有较高的预测精度。在传感器发生漂移偏差故障后，实际输出和预测输出之间的残差值慢慢变大。当系统继续运行了一段时间后，该残差值大于设定的阈值，此时可以断定该传感器已经发生了故障，应立即切断该路输出。从上述结果可以看出该神经网络有较高的诊断准确度。

在不完全微分PID控制下，转速分别为5 100 r/min和12 000 r/min时，人为切断4#传感器信号线，切断前后2#和4#传感器输出变化分别如图13和图14所示。

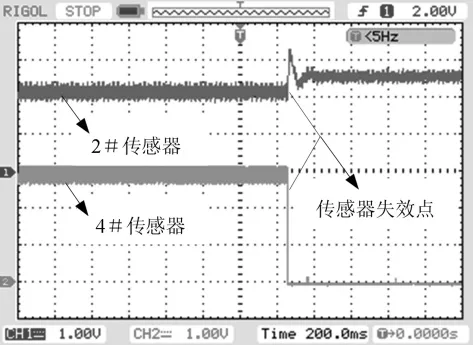
图13 5 100 r/min时传感器输出Fig.13 Sensor output at 5 100 r/min

从图13和图14可以看出，在切断4#传感器瞬间2#传感器输出跳变值都比较小，远小于允许最大跳变值(±2.5V)，说明当4#传感器发生故障时，系统仍能安全稳定的运行;另外，图13中2#传感器输出跳变比图11稍大一点，这是由于转速5 100 r/min处在一阶弯曲临界转速附近［10］。

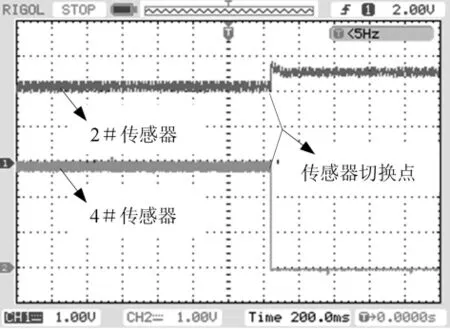
图14 12 000 r/min时传感器输出Fig.14 Sensor output at 12 000 r/min

通过动态信号频率分析仪(35 670 A)可实时记录2#和4#传感器的输出。当分别在5 100 r/min和12 000 r/min人为切断4#传感器信号线时，2#传感器同频输出随转速的变化分别如图15、图16所示。

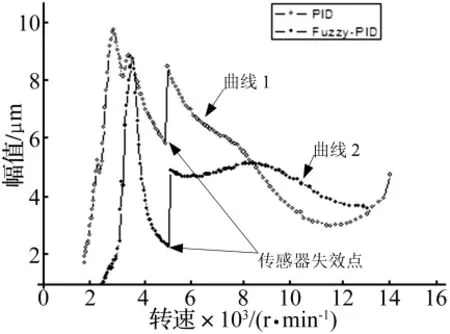
图15 5 100 r/min时2#传感器的同频输出Fig.15 Output of 2#sensor at 5 100 r/min

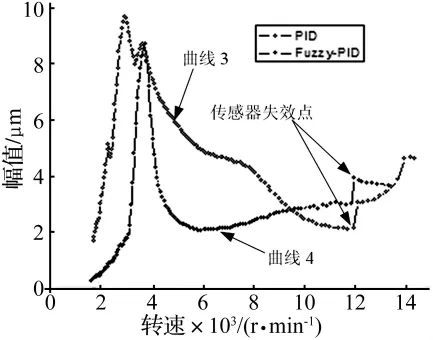
图16 12 000 r/min时2#传感器的同频输出Fig.16 Output of 2#sensor at 12 000r/min

其中，曲线1和曲线3为PID控制下振动曲线，曲线2和曲线4为模糊PID控制振动曲线。从图中结果可以看出，在5 100 r/min切断4#传感器信号线时，2#传感器测量位置处转子振动出现较大的跳变，但转子未出现失稳;在12 000 r/min切断4#传感器信号线时，2#传感器测量位置处转子振动跳变较小，这说明在切断4#传感器后转子能够继续安全地运行;另外，图中曲线2和曲线4的振幅比曲线1和曲线3的振幅小，这说明模糊PID控制效果比不完全微分PID控制效果略好。

5 结论

对传感器进行冗余设计可提高磁悬浮轴承转子系统的可靠性。根据对传感器冗余的磁悬浮轴承转子系统的联合仿真和试验验证，结论如下:

(1)本文所设计的模糊PID控制器的控制效果要优于不完全微分PID的控制效果。

(2)通过双传感器输出平均可减少传感器测量点和磁悬浮轴承施力点不一致问题对系统动态性能的影响。

(3)在系统运行过程中，当某一传感器发生故障失效时，根据本文设计的传感器故障诊断方法，能够及时准确地诊断出故障传感器，同时系统仍能安全平稳的运行，以此验证了采用传感器冗余设计可以提高系统可靠性的结论。

［1］胡业发，周祖德，江征风.磁力轴承的基础理论及应用［M］.北京:机械工业出版社，2006.

［2］Younggyu M D N，Cho S R，Kyung J H，et al.Design and implementation of a fault-tolerant magnetic bearing system for turbo-molecular vacuum pump［J］.IEEE/ASME Transactions on Mechatronics，2005，10(6):626 －631.

［3］Kim S J.On-line diagnosis of sensor faults in active magnetic bearing system equipped with built－in force Transducers［D］.KAIST，1998.

［4］周祖德，库少平，胡业发.电磁轴承多传感器故障诊断研究［J］.中国机械工程，2005，16(1):57－59.

［5］崔东辉.高可靠性磁悬浮轴承系统关键技术研究［D］.南京航空航天大学，2010.

［6］牟伟兴，谢振宇.磁悬浮轴承柔性转子系统变参数控制［C］.第三届全国磁悬浮会议，2009:55－62.

［7］Schweitzer G.虞 烈，袁崇军，译.主动磁轴承基础、性能及应用［M］.北京:新时代出版社，1997.

［8］李增刚.ADAMS入门详解与实例［M］.北京:国防工业出版社，2006.

［9］窦忠才，谢振宇.带阻尼器磁悬浮轴承柔性转子系统动态性能的研究［C］.第三届全国磁悬浮会议，2009:55－62.

［10］牟伟兴.磁悬浮轴承柔性转子系统变参数控制［D］.南京:南京航空航天大学，2010.

［11］Zhang J G，Hu Y F，Wu H C，et al.Co-simulation of magnetic suspended rotor system:research and application［C］. International Conference on Mechatronics and Automatio，2009:1711 － 1715.

［12］肖鹏飞，谢振宇.基于ADAMS-MATLAB的磁悬浮轴承转子系统联合仿真［J］.系统仿真技术，2011，7(1):48 －53.