飞机滑行作用下水泥混凝土道面板动响应分析

翁兴中，寇雅楠，颜祥程

(空军工程大学 工程学院，西安 710038)

机场道面除停放飞机外，还要保证飞机在其上滑行、起飞、着陆。飞机滑行时对道面产生的作用最大［1］。目前，在机场水泥混凝土道面板厚度设计时，将这种移动荷载作用下道面的受力特征，用作用在道面板上的静载乘以动载系数来表示，然后按静力分析方法进行计算。为了研究飞机动、静荷载之间的差别，需要对移动荷载作用下道面板的响应进行分析。1961年，Члущков采用无阻尼的 Winklen地基模型，把飞机—道面板—土基体系看作是一个自由度的振动问题。美军工程兵Waterways试验站［2］对柔性道面和刚性道面在飞机动荷载作用下的应力和挠度进行了大量实测工作，但没有给出理论计算方法。Vajarasathira等［3］把道面板作为梁来处理，并假设地基是线粘弹性休，由结构阻抗法导出直接数值解法。黄晓明等［4］采用Green函数法求得了移动荷载作用下板稳态挠度和瞬态挠度的积分解析解。孙璐等［5－6］对粘弹性文克勒地基在移动荷载作用的力学进行了分析。蒋建群等［7］采用移动荷载作用下Kelvin地基上的无限大板作为力学分析模型，分析了运动车辆荷载作用下路面体系的动力响应。娄平等［8－10］对粘弹性地基上的长梁进行了研究。以上的研究成果较好地解决运动荷载作用下粘弹性地基上板的响应分析问题，但在板的结构和地基类型上与目前国内军用机场水泥混凝土道面设计［11］所采用的模型的差别较大，无法解决在机场水泥混凝土道面结构设计中动响应问题。

本文应用半解析元法，建立了粘弹性层状地基上四边自由的矩形道面板的力学计算模型;对飞机滑行时对道面板作用的荷载进行了研究;计算了飞机滑行作用下道面板的响应。此外，提出了道面板动挠度的测定方法，在某机场对H－6飞机以不同速度滑跑时，道面板的动挠度进行了实测，并将实测结果与计算结果进行对比分析。

1 计算方法

机场水泥混凝土道面是由四边为接缝相连接的板块所组成，结构分为面层、基层(垫层)和土基。为了简化计算，将面层视为四边自由的单块板。飞机在道面上滑行时，其作用在道面上的位置是发生移动的，形成了移动荷载。这种移动荷载相对于道面某一点，其作用的时间是很短的;考虑基层(垫层)和土基材料本身的变形特性，将基层(垫层)和土基视为粘弹性层状体系。计算模型如图1所示，并作如下假定:

(1)水泥混凝土道面板为各向同性的等厚板。

(2)基层(垫层)和土基为粘弹性层状体。

(3)道面板与基层之间为光滑接触，基层(垫层)与土基之间为连续接触［12］。

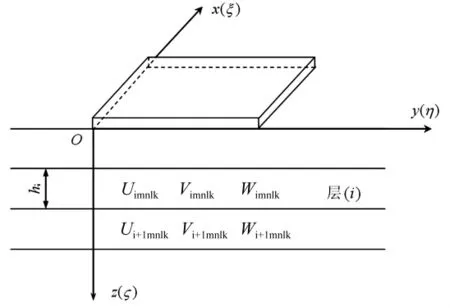
图1 计算模型Fig.1 Calculation model

为了便于分析，采用相对坐标 ξ、η、ζ，令:

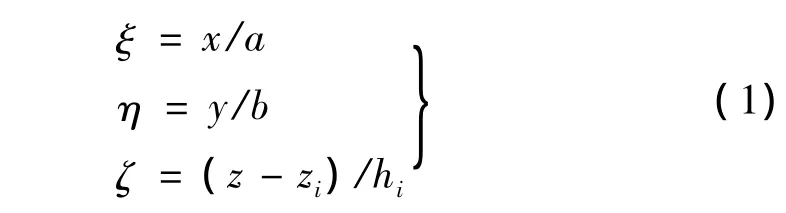
式中:a为板在x轴方向上的长度;b为板在y轴方向上的长度;zi为第i层层元上结面的z轴方向的坐标;hi为第i层层元的厚度。

对于基层和土基采取分层的方法(见图1)，则第i层的位移函数为:

板作为特殊的层元，采用如下的位移函数:

式中:Xm(ξ)，Yn(η)分别是ξ和η方向上满足两端自由梁的振型函数;Uimnlk，Vimnlk，Wimnlk，Ui+1mnlk，Vi+1mnlk，Wi+1mnlk和W0mn为待求系数。

Xml(ξ)，Ynk(η)分别由两部分组成，一部分是两端自由梁的振型函数Xm(ξ)，Yn(η)组成;另一部分是由衰减函数组成，其表达式为:

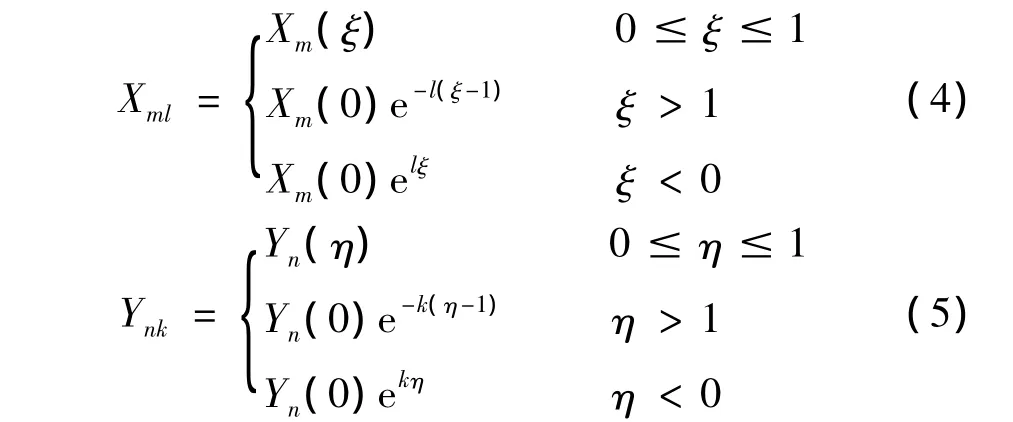
根据假定(3)，板与基层顶面的竖向位移连续，则:

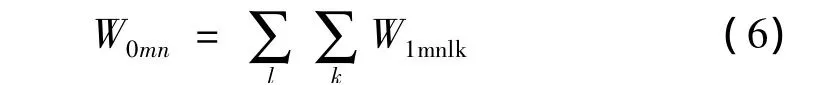
由式(6)可知，板的位移可以用基层顶面的竖向位移(即第1层顶面位移)来表示。因此，道面结构体系的未知参数为:

式(3)可表示为:

其中，

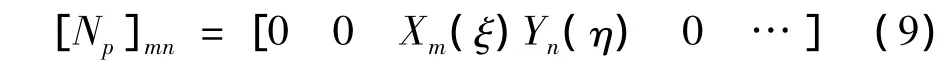
式(2)可表示为:

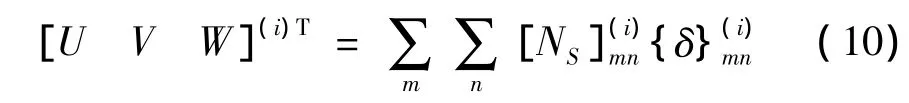
式中:

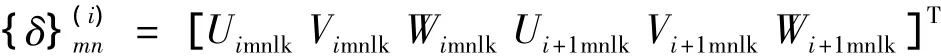
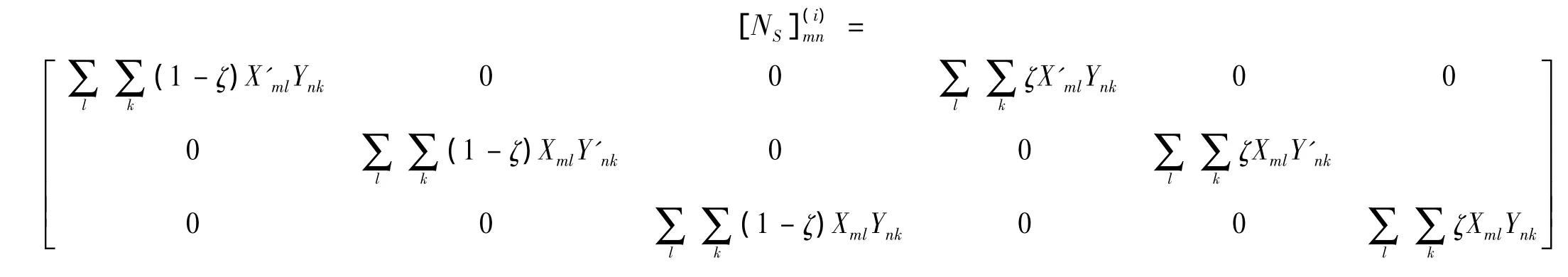
水泥混凝土板的应变为:

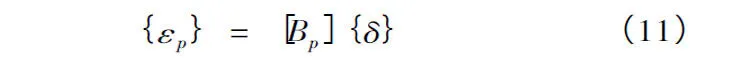
其中:［Bp］为水泥混凝土板的几何矩阵，按下式计算:

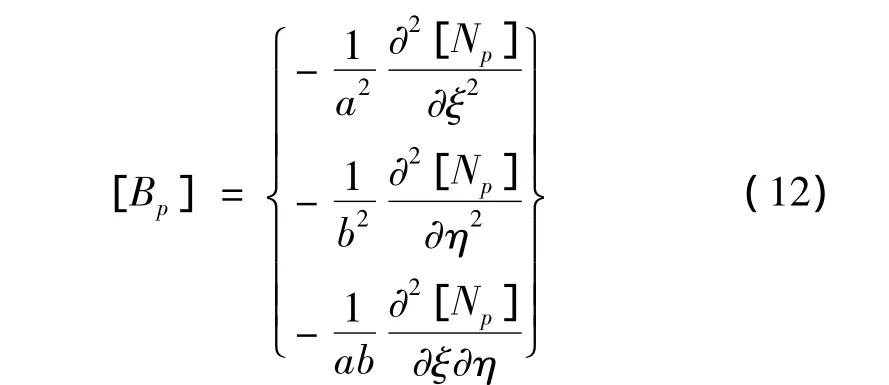
第i层元中的应力应变关系为:

与此产生的动应力按下式计算:

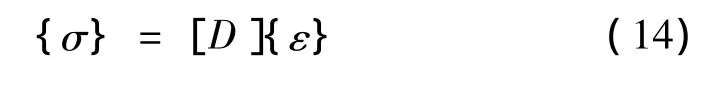
其中，［D］为弹性矩阵，水泥混凝土板的弹性矩阵为:

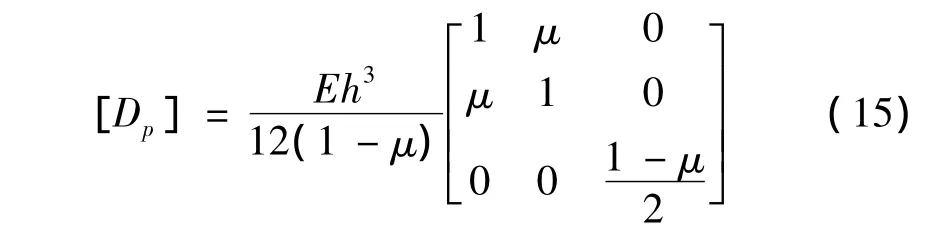
式中:E，μ，h分别为水泥混凝土板的弹性模量、泊松比、厚度。

第i层元的弹性矩阵为:

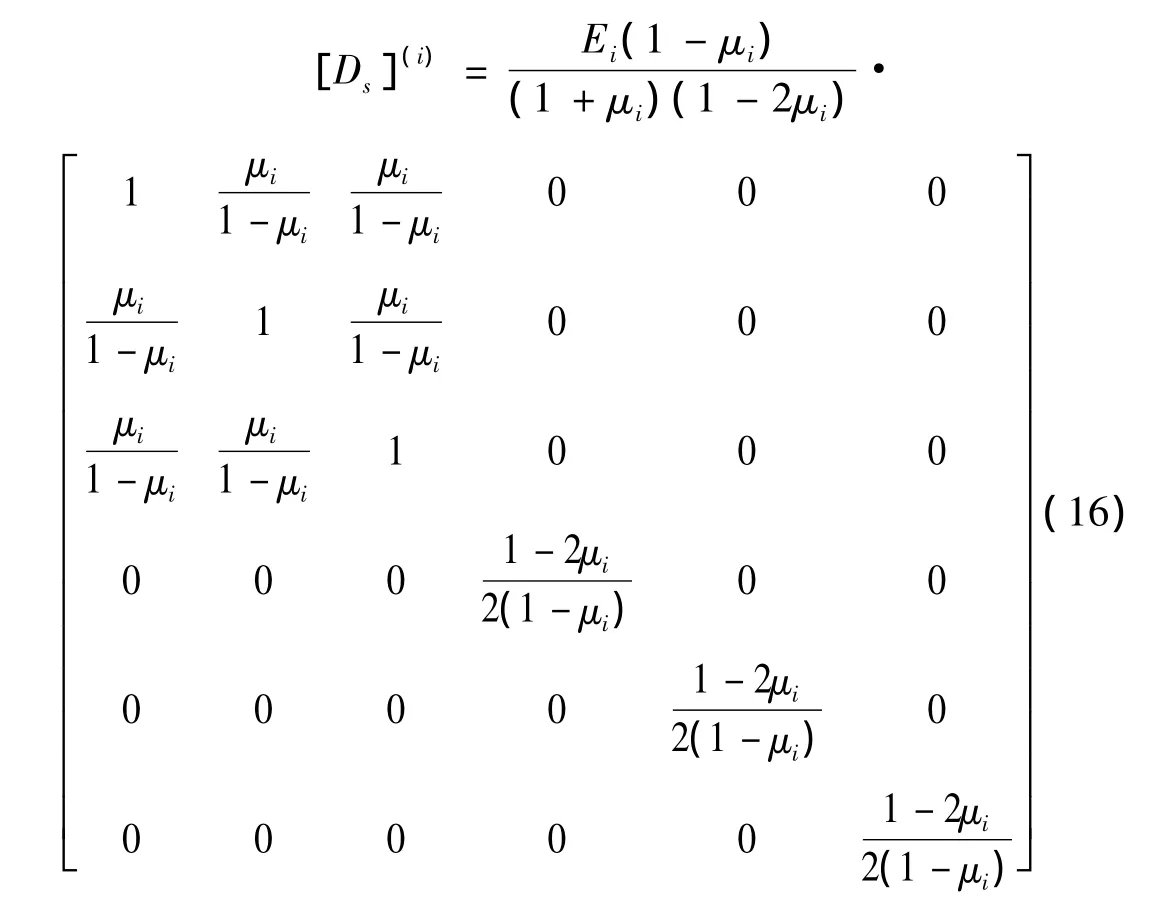
式中:Ei，μi，hi分别为第 i层层元的弹性模量、泊松比、厚度。

水泥混凝土道面板的刚度矩阵为:

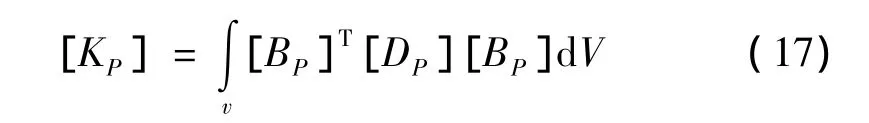
第i层层元的刚度矩阵为:

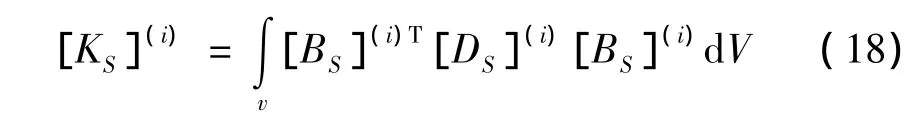
在此基础上，集合成整体刚度矩阵:

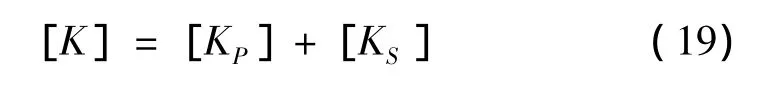
类似地可以建立起水泥混凝土道面板的质量矩阵:

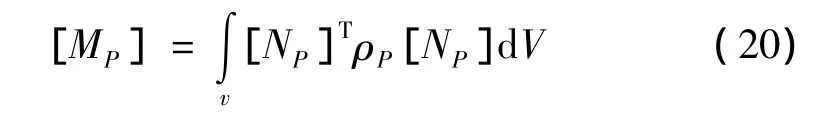
第i层层元的质量矩阵:

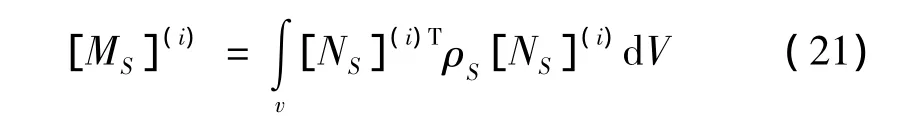
在此基础上，集合成整体质量矩阵:

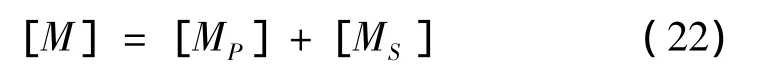
将板、基层(垫层)和土基所产生的阻尼等效为当量综合阻尼。该阻尼可用瑞尼阻尼表示，其阻尼矩阵为:

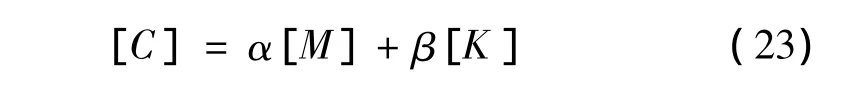
式中:α，β与道面结构体系振型有关的阻尼比。

当飞机在道面上滑行时，其作用在道面上的荷载属于表面力，而且仅与板层元有关，与基层(垫层)和土基无关。荷载列阵可按下式计算:式中:P→为作用在板上的表面力。

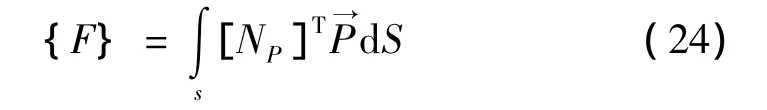
根据汉弥登原理建立起道面结构体系的运动方程:

求解式(25)就可以得到{δ}。按式(8)计算道面板的飞机滑行作用下的动位移，按式(10)计算第i层层元中的动位移;按式(11)计算水泥混凝土板的动应变，按式(13)计算第i层层元中的动应变;并按式(14)计算相应的动应力;从而分析道面结构在飞机滑行作用下产生的动响应。

2 道面板动挠度实测

在陕西某机场对H－6飞机不同滑行速度下道面板的动挠度进行了实测。采用的位移传感器为变磁阻式位移传感器，记录仪为KV－Ⅰ型微变形自动监测仪，它能根据设定的位移值自动进行记录。该机场道面板分块尺寸为6 m×4 m，四边为企口接缝，板厚为0.24 m，基层为0.24 m砂砾石基础。在距跑道端部490 m处相邻的三块板内共布置了13个测点(见图2)。9～13号测点主要是根据所测得的道面板变形曲线判断飞机滑行通过道面板的位置;2，3号和7，8号主要测定接缝传荷系数对动挠度的影响;其它测点主要是测定道面板的动响应。每个测点在道面结构中的埋设方式见图3。该埋设方法保证了位移传感器在飞机荷载作用下自身不产生移动，并对飞机滑行通过时能自动量测。这次测试共进行两项内容:

(1)飞机停放在道面板上的所产生的挠度，所测得的数值作为进行动效应分析的基准;

(2)飞机以不同滑行速度通过道面板时，道面板的挠度随时间变化规律，所测得的数据作为道面动响应分析的依据，同时验证理论分析方法的正确性和有关计算参数的确定，为理论分析奠定基础。

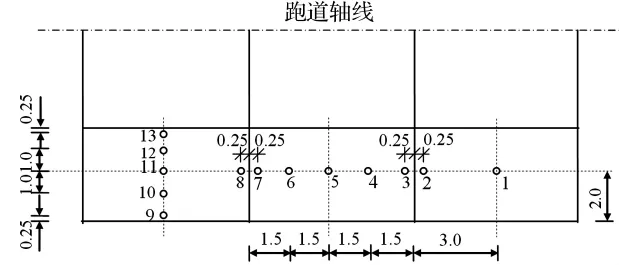
图2 位移传感器平面布置图(单位:m)Fig.2 Floor chart of transducers(unit:m)

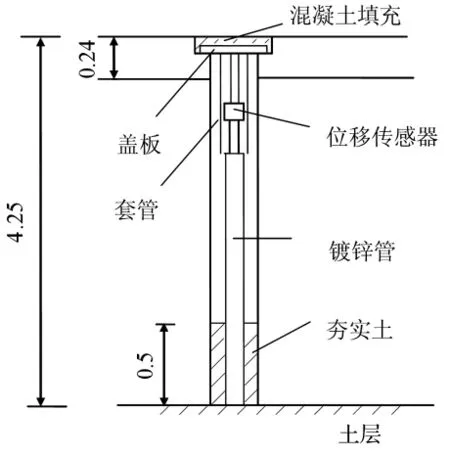
图3 位移传感器埋设方式(单位:m)Fig.3 Installed method of transducer(unit:m)

3 动响应分析

飞机在道面上滑行时，作用在道面上的荷载主要是由两部分组成:一是飞机自身的重量G;二是飞机滑行时产生的升力Fs，其算式为:

式中:Cy为升力系数;S为机翼面积;ρg为空气密度;v为飞机滑行速度。

可以根据飞机的离地速度计算飞机不同滑行速度时的升力。飞机滑行时作用在道面板上的荷载P由自身重量和滑行产生的升力组成，算式为:

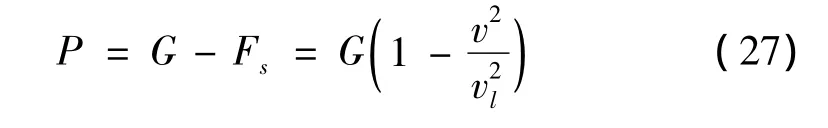
式中:vl为飞机的离地速度。

道面结构的计算参数:道面板，Ec=35 000 MPa，μc=0．167，ρP=2 400 kg/m3;基层，E1=210 MPa，μ1=0．3，ρ1=2 100 kg/m3;土基，E0=80 MPa，μ0=0．3，ρ0=1 800 kg/m3。对式(25)求解采用逐步积分法的Wilson－θ法。在Wilson－θ法中，随着步长(v×t)的减少，其结果逐渐收敛。从计算结果可知，当步长取0．5 m时，其挠度和弯矩值趋向稳定，且收敛于正确解。

不同的α，β取值表示道面结构的不同阻尼。计算结果(见图4)表明:道面板的动挠度变化与β的取值有较大的关系，与α取值关系较小。阻尼的改变主要影响道面板挠度变化曲线的形状和滞后性。当β较小时，板边(见图2(a))出现波动现象，发生的滞后性较小。随着β的增加，波动现象减少，滞后性增大。当α =0．5，β =0．05 时，波动现象完全消失。

图5为实测结果与理论计算结果的对比，从图中可以看出:无论是从其峰值，还是变化规律来看，两者的吻合程度是相当高的，说明本文所建立的道面板动响应的计算方法可以反映道面的实际工作状况，可用来进行道面板的动响应计算。从计算结果还可得出:板中的吻合程度较板边的吻合程度要高，说明了板的边界条件对板中的影响较小，对板边的影响较大。因为在本文的计算方法假定板的边界条件为自由边，而

图4 动挠度与阻尼的关系Fig.4 Relationship of dynamic deflection and damp

可以根据飞机的离地速度计算飞机不同滑行速度时的升力。飞机滑行时作用在道面板上的荷载P由自身重量和滑行产生的升力组成，算式为:实际板的边界条件介于自由和铰接之间。板边的动挠度要大于板中的动挠度。从荷载在道面板上作用的时间与动挠度的关系来看，动挠度有明显的滞后性，说明道面结构存在着较大的阻尼。飞机滑行通过道面板时，道面板上不同位置的动效应是不同的，板边的动效应要大于板中。这是因为，板中的结构强度一般要高于板边的结构强度，板中的阻尼特性表现得更突出。

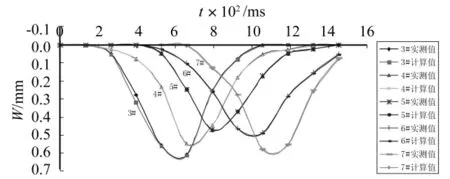
图5 计算值与实测值对比Fig.5 Comparisons of calculation and experiment data

图6为道面板各点的动挠度随飞机滑行速度的变化规律。在板边(x=0)，其动挠度出现了波动现象，说明了突加荷载的影响。道面板不同点随着飞机滑行速度的变化规律是不同的。靠近板边时，其动挠度随着滑行速度的增大而减小;而靠近板中(x=1.5 m，3.0 m)时，其动挠度先随着滑行速度的增大而增大，但达到某一速度时，则随着滑行速度的增大而减小，说明其动挠度随着滑行速度的变化存在着极值。这种现象的出现是飞机滑行过程中产生的升力引起的。飞机的升力与飞机滑行速度的平方成正比，在滑行速度比较小时，飞机的升力产生很小，飞机对道面结构的作用主要是由其自身重量产生的，此时的升力可以忽略不计。由于飞机的滑行在道面上产生动力效应，使得道面结构的动响应会大于静响应，即出现极值，其极值出现的速度为20 km/h左右。随着飞机滑行速度的增大，所产生的升力加速增大，对道面作用的荷载也相应地减小，产生的动挠度也随之减小，基本呈线性关系。板边位置的动挠度没有出现极值的原因是板边为自由边，飞机荷载的作用类似为冲击力的作用。相对而言其荷载的作用时间较短，由于阻尼的作用，没有足够的荷载作用时间使道面的挠度得到完全产生。这种现象随着滑行速度的增大而越明显，因此随着滑行速度的增大道面产生的动挠度逐渐下降。

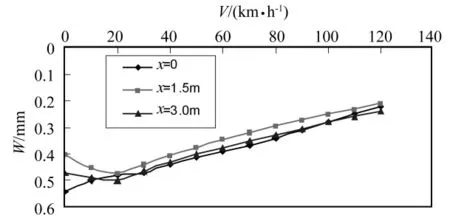
图6 动挠度与飞机滑行速度曲线(y=2.0 m)Fig.6 Curves of dynamic deflection and airplane taxing

4 结论

研究了飞机滑行时，粘弹性层状地基上道面板的动响应。采用的半解析元法较好地解决了粘弹性半空间地基与道面板的相互作用。计算方法较其它数值计算方法具有未知变量少，计算速度和收敛快等特点。建立了飞机在道面上滑行的荷载计算公式。运用瑞尼阻尼表示整个道面结构体系的阻尼特性，使道面结构的阻尼特性得到简化。用Wilson－θ法求解运动方程组，得到板的挠度变化曲线。在道面内部钻孔安装位移传感器，解决了道面板动挠度的测定方法。实测了H－6飞机在不同滑行速度下，道面板挠度随时间的变化规律。实测结果与计算结果误差在3%以内。说明本文所建立的道面板动响应分析方法是正确的，可用来进行道面结构动响应的分析，为机场水泥混凝土道面结构设计中动载系数的确定奠定了理论分析基础。

［1］翁兴中，蔡良才.机场道面设计［M］.北京:人民交通出版社，2007:22 －23.

［2］Hom W J.Pavement response to aircraft dynamic loads［R］.ArmyEngineerWaterwaysExperimentStation，Defense Technical Information Center，1975.

［3］Vajarasathira K V，Yener M，Ting E C，et al.Aircraft pavement interaction in runway analysis［J］.Journal of Structure Engineering，1984，110(5):1008－1020.

［4］黄晓明，邓学钧.移动荷载作用下粘弹性文克勒地基板的力学分析［J］.重庆交通学院学报，1990，9(2):45 －51.HUANG Xiao-ming， DENG Xue-jun. Themechanical analysis of plate on visco-elastic winkler foundation under moving load［J］.Journal of Chongqing Jiaotong University，1990，9(2):45－51.

［5］孙 璐，邓学钧.运动分布荷载作用下弹性地基上无限大板瞬态响应［J］.应用力学学报，1997，14(2):72－78.SUN Lu，DENG Xue-jun.Transient response for infinite plate on winkler foundation by a moving distributed load［J］.Chinese Journal of Applied Mechanics，1997，14(2):72－78.

［6］孙 璐，邓学钧.运动负荷下粘弹性Kelvin地基上无限大板的稳态响应［J］.岩土工程学报，1997，19(2):14－22.SUN Lu，DENG Xue-jun.Steady response of infinite plate on viscoelastic winkler foundation to moving load［J］.Chinese Journal of Geotechnical Engineering，1997，19(2):14 －22.

［7］蒋建群，周华飞，张土乔.移动荷载下粘弹性地基上无限大板的稳态响应［J］.中国公路学报，2006，19(1):6－11.IANG Jan-qun，ZHOU Ha-fei，ZHANG Tu-qiao.Steady state response of infinite plate on visco-elastic foundation subjected to moving load［J］.China Journal of Highway and Transport，2006，19(1):6 －11.(in Chinese).

［8］娄 平，曾庆元.移动荷载作用下连续粘弹性基础支承无限长梁的有限元分析［J］.交通运输工程学报，2003，3(2):1－6.LOU P，ZENG Q Y.Finite element analysis of infinitely long beam resting on continuous viscoelastic foundation subjected to moving loads［J］.Journal of Traffic and Transportation Engineering，2003，3(2):1 －6.

［9］娄 平，曾庆元.移动荷载作用下板式轨道的有限元分析［J］.交通运输工程学报，2004，4(1):29－33.LOU Ping，ZENG Qing-yuan.Finite element analysis of slab track subjected to moving load［J］.Journal of Traffic and Transportation Engineering，2004，4(1):29 －33.

［10］聂志红，阮 波，李 亮.铁路道床路基动力响应的参数影响［J］.交通运输工程学报，2004，4(1):34－37.NIE Zhi-hang，RUAN Bo，LI Liang. Dynamic response parameters of railway ballast-subgrade［J］.Journal of Traffic and Transportation Engineering，2004，4(1):34－37.

［11］GJB 1278A－2009.军用机场水泥混凝土道面设计规范［S］.

［12］赵炜诚，许志鸿，黄 文.混凝土面层与贫混凝土基层的层间作用对荷载应力和弯沉的影响［J］.中国公路学报，2003，16(4):9－15.ZHAO Wei-cheng，XU Zhi-hong，HUANG Wen.Influence of load stress and deflection on interfacial interaction between portland concrete pavement and lean concrete base［J］.China Journal of Highway and Transport，2003，16(4):9－15.