用哲学观点驾驭空间几何中数学思维的理性

●凌云志 (黄山区教育局教研室 安徽黄山 245700) ●洪新华 (黄山市教科所 安徽黄山 245000)

很多学生怕学空间几何，是因为空间几何抽象难以萌发数学的直觉.如果能静心反思课堂教学和学生解题时的困惑，那么归因就不那么简单.诚然，与空间相关的基本概念、公理、定理和基本模型是学好此课的基石;典型问题的演练是培养学生学习与解题能力的重要途径.笔者认为，很多空间几何课堂教学缺失了赋予学生体验数学智慧的经历，这种智慧被我们定格于演绎推理形式逻辑所吞噬，空间思维需要“运动与相对静止”、“相互联系与转化”等哲学观来统领，让学生学到理性驾驭思考问题的经验.

纵观教材：点、线、面、体概念的建立，点动成线、线动成面、面动成体;面面相交成线、线面相交或线线相交成点;线线平行(垂直)与线面平行(垂直)或面面平行(垂直)互化等，足以说明：空间从本质上是运动、变化、联系的.基础知识只是赋予了空间结构与空间元素基本的数学联系(本质)，它是相对静态的和独立的，即哲学意义上的相对静止.有些基本的(概念、定义、公理和定理)知识放归于多样复杂的空间问题时，教师必须借助运动变化、联系转化的观点，展示认识空间数学本质有序性和方法性，让学生真实体验到基本知识的价值与意义(知识的活化).因而，巧妙、适宜地变化题境，展示空间元素运动、变化、联系、生成的生动画面，促使学生空间观念有效形成与发展.在教学中，应注意以下几个方面：

1 运动生成

例1 给定异面直线a，b和点P，令直线a，b所成的角为θ，问过点P能作几条直线满足：与直线a所成的角为锐角α且与直线b垂直.

点拨 如图1，过点P作 a'∥a，b∥b'，过点 P 与直线 a'所成的锐角α的直线，以及过点P与直线b'垂直的直线，它们形成的空间图形各是什么?

意义 过点P与直线a'所成的角为锐角α的所有直线的集合，是以a'为轴，2个对顶的锥角为2α的“无底圆锥”侧面，设其曲面为S;过点P与直线b'垂直直线的集合，是以b'为法线，过点P的平面β.符合条件的空间元素运动生成特定空间：曲面S是过点P绕a'轴旋转而成，平面β是取一条过点P与直线b'垂直的直线绕点P旋转而成.

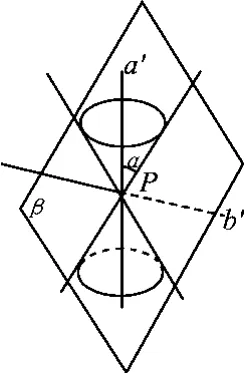
图1

空间元素从“无形”明晰出“有形”、局部拓展成全部、个体演绎为总体，这是空间观念存在并能动地再现概念属性的体现，是探究空间几何问题能力的基础，是教师首要追寻的教学目标.

觉悟 若90°-θ＜α，则S∩β是2条直线，满足题设的直线可作2条;若90°-θ=α，则平面β与曲面S切于1条直线，满足题设的直线仅可作1条;若90°-θ＞α，S∩β=φ，则满足题设的直线不存在.

2 以静制动

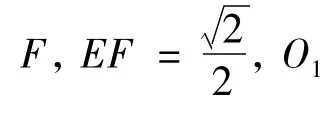
图2

(1)三棱锥A-BEF的体积是否变化;

(2)异面直线AE与BF所成的角是否变化;

(3)二面角E-AB-F是否变化;

(4)二面角A-EF-B是否变化;

(5)二面角A-EB-F是否变化;

点拨 (1)从定点A，B观察线段EF，结合面积、体积度量要素，能做出哪些判断?

(3)如何延展△ABF和△ABE所代表的“局面”，显现二面角E-AB-F;

(4)注意变化的△AEF，△BEF所在的面;

(5)注意二面角A-EB-F与二面角A-EB-D之间的关系.

意义 感悟“动中有静”、“变中有定”，相对静止是认识事物的重要方法;学会以静制动，用“定”思“变”.

发现具特殊意义的空间背景或对象，从而找到解决问题的方法与思路，诱发空间观念以追寻数学意义或价值之目标意识，这应成为教师培养学生空间思维能力的关键.

觉悟 (1)如图2，点A到EF距离不变，S△AEF为定值，点B到平面AB1D1距离不变，于是动点E，F不引起VA-BEF变化.

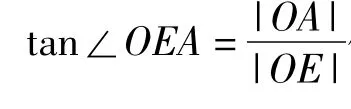
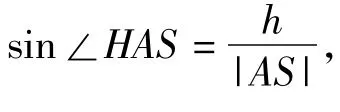
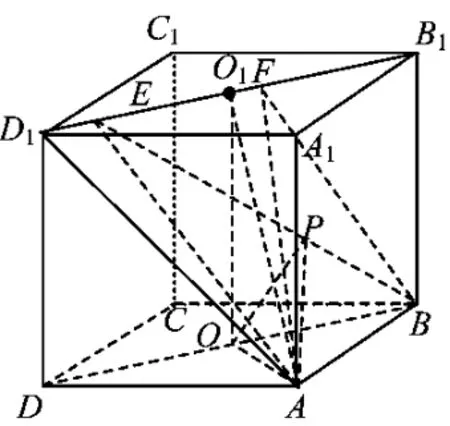
图3

基于适用于水利建设的地理水纹记号系统化研究，本文提出了系统化的研究方法及流程，把视觉传达设计运用于具体的水利水纹记号改良设计。我国现代水利中的地理水纹记号还有待于规范、完善，这对于我国水利现代化建设以及水文化发展具有重大现实意义。

3 化静为动

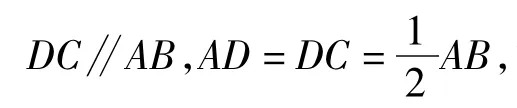
(1)若DA⊥平面APB，试问：平面APC⊥平面ABCD成立吗?

(2)若AP⊥平面ABCD，试问：你能探究出哪些结论?在什么位置作出二面角A-PB-C为宜?

(3)若PC⊥BC，试问：平面APC⊥平面ABCD是否成立?是否有AP⊥平面ABCD成立?

点拨 (1)在DA⊥平面APB条件下，在平面APB内，过点B作P'B⊥AB，你能发现∠P'CB的特殊意义?

(2)在AP⊥平面ABCD的条件下，能否从线面垂直去发现更多有关面面垂直或线线垂直的结论?

(3)在PC⊥BC的条件下，为探究AP⊥平面ABCD成立与否，注意点P有无可变化余地.

意义 题设往往赋予空间的可变性，对验证猜想是否合理至关重要;感觉到空间的可变性就是发挥空间观念探究问题能动意识，教师诱发“可变”赢得学生主动“可为”.

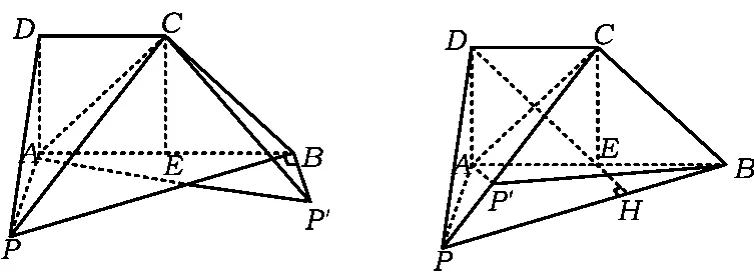
图4 图5

觉悟 如图4，由附加条件(1)和点拨(1)，易证：P'B⊥平面ABCD，AC⊥CB，从而∠P'BC为P'-AC-B的平面角，由△P'CB是直角三角形，∠P'BC是锐角，知平面APC⊥平面ABCD不一定成立.

(2)如图5，由题设及AP⊥平面ABCD可得：①平面APC⊥平面ABCD，平面APD⊥平面ABCD，∠DAC为二面角D-PA-C的平面角.②BC⊥平面APC，∠ACP为P-BC-A的平面角;在平面APB内作EH⊥PB，点H为垂足，联结CH，∠CHE即为二面角A-PB-C的平面角.

(3)如图5，联结DE，易证DE∥CB，由题设及PC⊥BC得DE⊥平面APC，平面APC⊥平面ABCD都成立;由于当点P在线段PC移动至某点P'时，不会改变题设条件，由AP位置的可变性，知AP⊥平面ABCD结论不一定成立.

4 关注特殊

图6

点拨1 能否弄清平面BEF与平面PAB在点B处的交线情况?因E，F分别是AD，PC的中点，故考虑EF与平面PAB和平面PBC的位置关系.

意义 矛盾的特殊性决定事物的性质，把握题设条件的特殊性是找准解题突破口、使空间观念具备锁定解题关键的数学视角，它是体现空间几何课堂有效教学的重要环节之一.

点拨2 EF∥平面PAB，对分析平面BEF与平面PAB在点B处交线位置有意义吗?

意义 由特殊性入手，继而引发对关联性的思考，使学生空间观念处于有序渐进、层层深入的探究氛围，这是教师孜孜以求的课堂教学艺术.

觉悟2 交线应与EF平行，过点B作BP'∥EF.

点拨3 根据EF⊥平面PBC，可知P'B⊥平面PBF，对明确平面BEF与平面PAB的夹角有帮助吗?

觉悟3 是∠PBF(得到它为45°，并不难).5 教育价值

数学课不仅仅要传授知识、教会方法、领悟思想和获得能力，还有一个更沉重的价值：对人的世界观形成与发展应产生积极的影响.我们应沉思为什么有那么多的学生厌恶数学，尽管成因复杂，但有一点，在高考的高压下，我们的数学课太急功近利，呈现的数学问题杂、难、快、多，很少有教师去思考：如何教会学生去品味、体验数学中蕴含的让人明智的哲理与从容的理性.把哲学的境界融入空间几何的课程中，旨在挖掘其教育功能.究其因，空间几何课程有太多的教育素材，如线线、线面、面面关系的转化，空间问题化归为平面问题，位置关系与数量关系的互化，都印证了哲学上事物是普遍联系又相互转化，而且这种联系与转化又带有某种规律.又如利用图形的特殊性质可以便捷地找出或求出二面角，这不正是灵验了把握特殊性是认识事物性质和解决问题的重要方法.再如，认真思考题设(诸如含45°、60°特殊角，有垂直或平行关系存在等)，巧抓偶然性，寻找解题的突破点，题设之偶然寓于问题结论求索的必然之中，等等.哲学给数学带来境界，也给数学送来获得智慧的经验与体验，为统领空间几何解题的观点、思想与方法带来了高度.