先分后合 化难为易
●臧玲娜 (浦江中学 浙江浦江 322200)
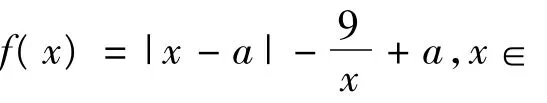
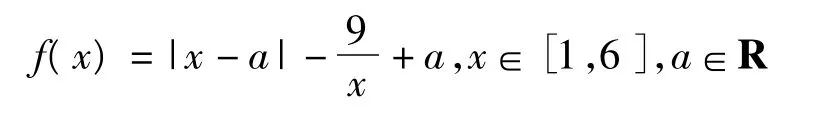
(1)若a=1,试判断并证明函数f(x)的单调性;
(2)当a∈(1,6)时,求函数 f(x)的最大值的表达式M(a).
(2010年浙江省数学会考试题)分析 (1)略.
(2)由这一含有参数的绝对值函数,由于受到旧有的固定思考模式的限制,真正能够把数形结合的思想方法用到这类题目当中的学生并不多,教师在分析问题时也没有结合得很好.笔者认为,应该打破旧有的固定模式,用“先分后合”的“五步法”来解决高中数学中常见而学生又甚感困难的含参绝对值函数的作图问题,以帮助学生加快作图速度,培养作图兴趣,从而提高学生数形结合的能力.

当1≤a≤3时,函数 f(x)在[1,a]上单调递增(如图1),在(a,6]上也单调递增(如图 2),从而f(x)在[1,6]上单调递增(如图3),即将图1中[1,a]的部分图像和图2中(a,6]的部分图像合在一起便可,把这种作图方法称为“先分后合”的方法.由图3可知,当1<a≤3时,f(x)在[1,6]上的最大值为 f(6)=4.5.
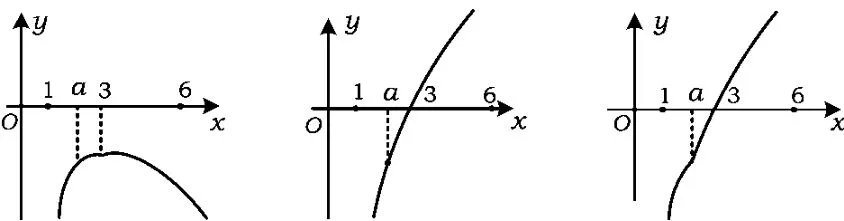
图1 图2 图3
用“先分后合”的方法也可以很方便地画出当3<a<6时的图像.
当3<a<6时,分段函数的2个表达式的各自图像如图4、图5所示,将图4中[1,a]的部分图像和图5中(a,6]的部分图像合在一起便得到了整个绝对值函数的图像.由图6可知,当3<a<6时,f(x)在[1,6]最大值为
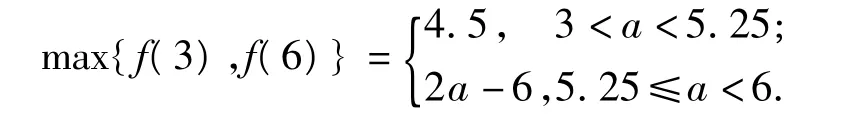

图4 图5 图6
由此可以总结出“先分后合”的方法作图的步骤:①分段写表达式:写出含参的绝对值函数的分段表达式;②分别作图:在各自坐标系内分别画出分段函数的几个表达式的完整图像;③确定分类:根据图像特征(主要是单调性)和各段函数的范围确定分类原则和方法;④截取图像:根据分类的标准截取各分段区间内的图像;⑤合成图形:把截取的几部分图像合成到新坐标系中,利用图像解题.
例2 设a为实数,函数f(x)=x2+|x-a|+1,x∈R.
(1)讨论f(x)的奇偶性;
(2)求f(x)的最小值.
(2002年全国数学高考试题)
分析 (1)略.
(2)按照“先分后合五步法解题”.首先分段写表达式

然后在各自坐标系内分别画出分段函数的2个表达式的完整图像.因为2段曲线的对称轴分别为x=0.5 和 x=-0.5,所以要分成 a≤ -0.5,-0.5<a<0.5和 a≥0.5进行讨论.
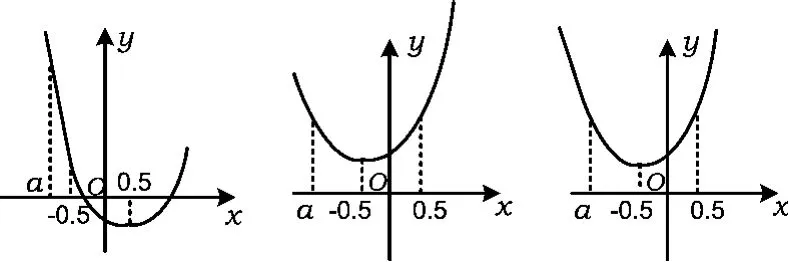
图7 图8 图9
①当a≤-0.5时,图7中(-∞,a]的部分图像和图8中(a,+∞)的部分图像合在一起得到图9,由图 9 可知 f(x)最小值为 f(-0.5)=0.75-a.
②当 -0.5<a<0.5时,图10中(-∞,a]的部分图像和图11中(a,+∞)的部分图像合在一起得到图12,由图12可知最小值为f(a)=a2+1.
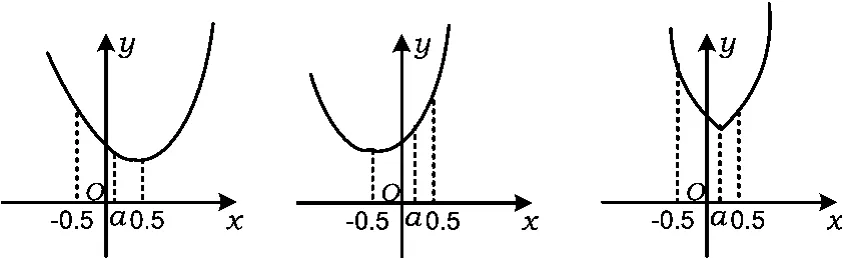
图10 图11 图12

图13 图14 图15
综上所述,

例3 已知a∈R,函数f(x)=x2|x-a|.
(1)当a=2时,求f(x)=x使成立的x的集合;
(2)求函数y=f(x)在区间[1,2]上的最小值.
(2005年江苏省数学高考试题)
分析(1)略.
(2)由题意得

①当a≤1时,图16中(-∞,a]的部分图像和图17中(a,+∞)的部分图像合在一起得到图18,由图 18可知在[1,2]上 f(x)的最小值为f(x)=1-a.

图16 图17 图18
②当 a∈(1,2]时,显然有
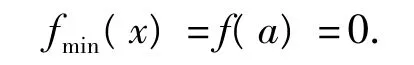
③当a>2时,由图19~21可知
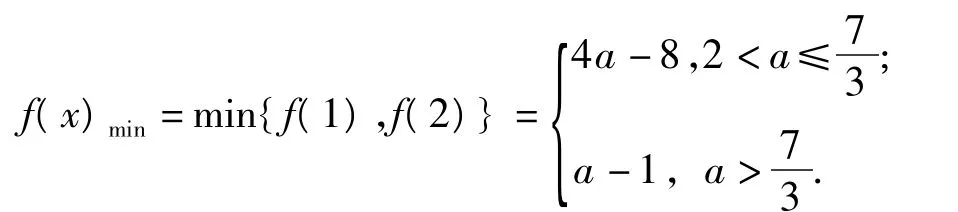
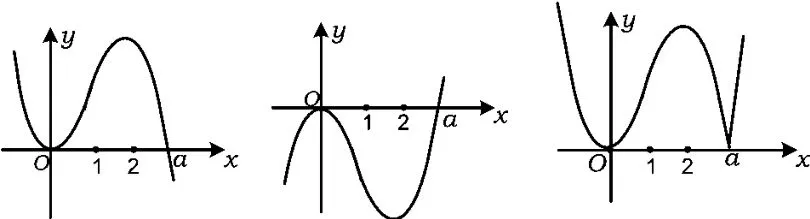
图19 图20 图21

当然,在运用“先分后合”的方法作图时要注意:分只是手段,合才是目的.分是为了合,如果能够清楚地作出整个图像就没必要分.同时在分与合的作图过程中,借助图像可以更形象、直观地理解为什么分类讨论,如何分类讨论.这是数形结合的新境界、新高度.

