圆锥曲线的一个统一性质的探究与引申
●王泳彩 (马寅初中学 浙江嵊州 312400)
由于椭圆、双曲线、抛物线是具有统一定义的圆锥曲线,因此它们具有许多统一的性质.笔者通过对2个问题的探究,得出几个有趣的结论.本文对圆锥曲线的研究是在标准方程下进行的,因此给出的性质也只对圆锥曲线的标准方程适用,至于非标准方程下的圆锥曲线还有待进一步研究.
1 定理的发现

问题2 过抛物线y2=2px(p>0)上一定点P(x0,y0)(y0>0)作2条直线分别交抛物线于点A(x1,y1),B(x2,y2).
(2004年北京市数学高考理科试题)
分析(1)略.
(2)设直线PA的方程为y-y0=k(x-x0),则直线PB的方程为y-y0=-k(x-x0).由

即直线AB的斜率为非零常数.
由问题1和问题2引发了以下思考:
(2)问题1和问题2的结论是巧合吗?对所有圆锥曲线这个性质是否都成立?
笔者借助几何画板研究发现,不管对椭圆、抛物线,还是双曲线,不管它们的位置如何,只要直线PA,PB的倾斜角互补,直线AB的斜率始终为定值.
限于高中阶段圆锥曲线的范畴,不妨设圆锥曲线统一的方程为Ax2+By2+Cx+Dy+F=0(A≠B且A,B不同时为0),P(x0,y0)为曲线上任一定点,过点P作倾斜角互补的2条直线PA,PB,与曲线的交点分别为 A(x1,y1),B(x2,y2).事实上,设直线PA方程为y-y0=k(x-x0),则直线PB的方程为 y-y0=-k(x-x0).由


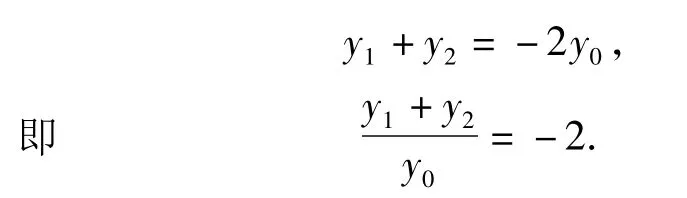
2 定理的引申
进一步思考,定值kAB与点P及圆锥曲线在几何上有什么联系呢?
如图1,可以设想将问题1中的直线 PA,PB不断绕点P旋转,逐渐使点A,B愈来愈靠近,最后可以得到点 A,B重合的状态.记点A,B重合的点为P0,用极限的观点来判断,此时直线AB应为曲线C的切线,点P0为切点.事实上,设线段AB的中点为M,则由PA,PB的倾斜角互补知PM⊥x轴或PM⊥y轴.当A,B重合于点P0时,点M与点P0也重合,故点P0为点P关于坐标轴的对称点,即点P0的坐标为(x0,-y0)或(-x0,y0).下面证明曲线C在点 P0处的切线与直线 AB平行.不妨设P0(x0,-y0),设切线方程为 y+y0=k(x-x0).由

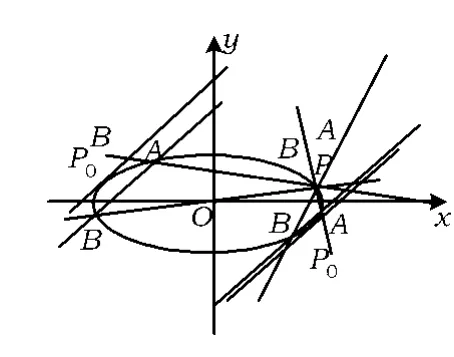
图1
故切线与直线AB平行.
同理可证曲线C在P0(-x0,y0)处的切线也与直线AB平行.对于双曲线与抛物线,证明过程类似.由此得到圆锥曲线的3个重要性质:
性质1 过圆锥曲线上任一定点P(x0,y0)(x0≠0,y0≠0)作倾斜角互补的 2 条直线 PA,PB,与圆锥曲线的交点分别为 A(x1,y1),B(x2,y2).若直线PA,PB的斜率都存在,则直线AB的斜率等于曲线在点P关于对称轴的对称点处的切线的斜率.
性质2 若直线y=kx+b(k≠0)与圆锥曲线C相交于点A,B(对于双曲线要求相交于同一支),则在曲线C上必存在定点P,使得直线PA与PB的倾斜角互补,且点P为将直线平移到与曲线相切时的切点关于曲线对称轴的对称点.
另外,设线段AB中点为M(x,y),则
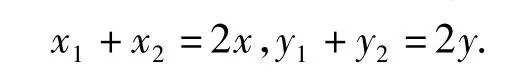
因为 A(x1,y1),B(x2,y2)在曲线上,所以

即线段AB的中点轨迹与曲线C的交点为(x0,-y0)和(-x0,y0).
由此也引出了圆锥曲线的另一个性质:
性质3 若直线y=kx+b(k≠0)与圆锥曲线C相交于点A,B,则在曲线C上必存在定点P,使得直线PA与PB的倾斜角互补,且点P为线段AB的平行弦中点轨迹与曲线的交点关于曲线对称轴的对称点.
3 定理的应用

(2011年嵊州市数学教师综合素质比武试题)
证法1 假设存在C上的一点M(m,n),则


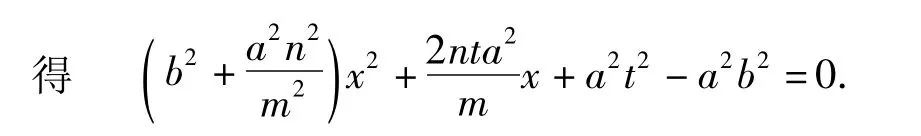
当m=0时,显然不可能.因为直线交C于点A,B,所以Δ>0,即

证法1计算量比较大,参加比武的数学教师也大都因为时间的限制与计算的繁杂,难以顺利求解.如果应用本文所得定理性质则可迎刃而解.
证法2 假设存在C上的一点M(m,n),则

当m=0时,显然不可能.

本文从常见的问题出发,将问题的结论作一般化推广和探究,再进一步地借助运动的观点和几何画板的演示,最终得出几个有趣的结论,揭示了定值kAB与点P的本质联系.这一探究过程,体现了新课程倡导的“突出数学本质,适当淡化形式和重思维、重探究、重过程”的理念.

