运用微积分求解物理问题的方法
杨国平
(绍兴市第一中学 浙江 绍兴 312000)
高考对物理学科提出了5种能力要求,其中之一是“运用数学知识解决物理问题的能力”.在新课程改革的背景下,简单的微积分已下放到高中数学课程中,这对物理学科的教学无疑是一大利好.
1 导数应物理而生
物理问题中经常会涉及到变化率,并在此基础上建立相应的物理概念,例如,在研究瞬时速度、加速度、角速度等概念的过程中,呼唤着导数的产生.导数是用来解决变化率的有效工具,瞬时变化率就是导数,其几何意义是切线的斜率,这在物理图像中经常涉及到.在有关内容已下放到高中数学以后,教师应该引导学生用导数来描述物理问题,这对学生准确理解物理概念、规律是很有好处的.经常用到的结论有:常数C′=0;幂函数(xn)′=nxn-1;三角函数(sinx)′=cosx;复合函数求导法则
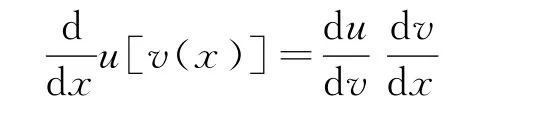
2 物理因导数而严谨
普通物理知识大多采用微积分来描述,而高中物理常把它们降解为初等的数学手段,但有些知识是很难回避微积分的,高中阶段往往一笔带过,这些知识自然就成为学生理解上的瓶颈.其实,只需引用简单的微积分常识(下面以三角函数sinθ为例),就可以圆满地解决不少问题.
2.1 简谐运动模型
质点的位移x随时间t的变化规律满足
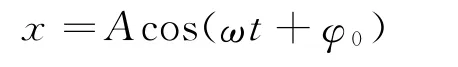
则其速度的变化规律为
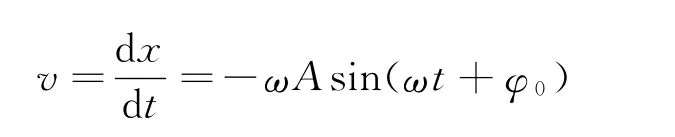
加速度

由此看到:做简谐运动的质点的位移、速度、加速度都是按正弦式规律变化的.另外
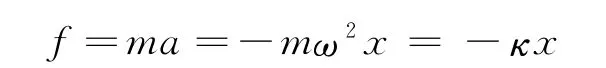
得到周期公式
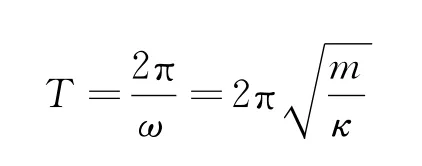
2.2 正弦交流电模型
线圈在匀强磁场中匀速转动,在中性面时记作t=0,穿过线圈的磁通量Φ=BScosωt,则线圈中的电动势
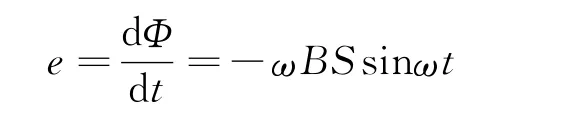
电流

若线圈有N匝,得到感应电动势的最大值为

(1)有效值:基于电流的热效应来定义.假设有一个定值电阻R,在交流的一个周期T内,产生的热量

代入得
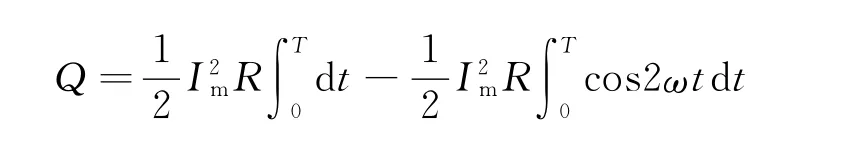
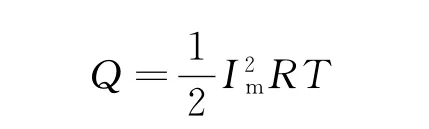
对照Q=RT,得到
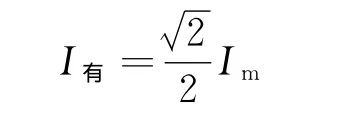
(2)LC振荡电路:通过电感线圈的电流为

则线圈两端的电压

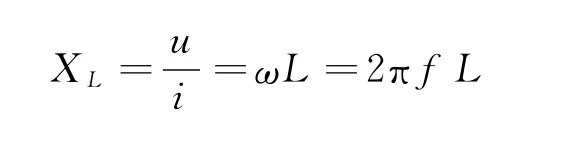
3 导数在物理题解中的应用
【例1】已知某质点的运动学方程为x=2t2+3t+4(单位:m),试求第1s末质点的瞬时速度、加速度.
解析:根据速度的定义
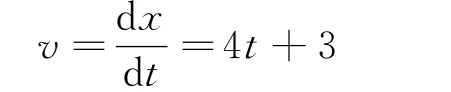
把t=1s代入得

加速度

可以证明,满足位移方程x=at2+bt+c的一定是匀变速直线运动,式中c为t=0时刻质点相对于原点的初始位置,质点的初速度等于b,加速度等于2a.
【例2】在水平地面上方10m高处,以20m/s的初速度沿斜上方抛出一物体,不计空气阻力,g取10 m/s2,求物体的最大射程[1].
解析:以抛出点为原点,建立水平、竖直方向的坐标系xOy,如图1,设v0与x轴的夹角为θ,飞行时间为t,有

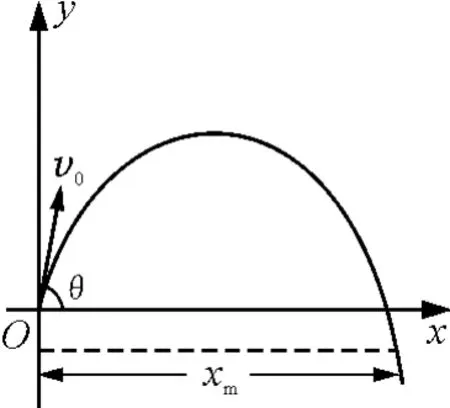
图1
联立(1)、(2)式消去参数θ,得
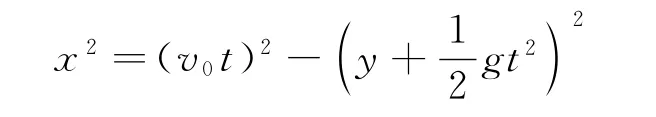
代入数据得

当x取最大值时,(3)式右边对t的一阶导数等于零,即
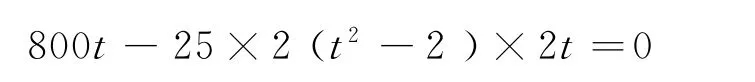
解得
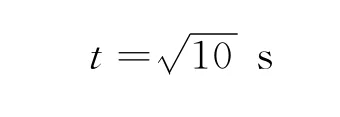
代入(3)式得
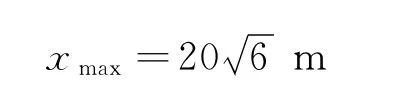
【例3】(2011年清华大学自主招生试题)如图2(a)所示,水平高台上有一小车,水平地面上有一拖车,两车之间用一根不可伸长的绳跨过定滑轮相连.拖车从滑轮正下方以恒定速度沿直线运动,则在拖车行进的过程中,小车的加速度
A.逐渐减小 B.逐渐增大
C.先减小后增大 D.先增大后减小

图2
解析:把拖车的速度分解为图2(b)所示的两个方向,小车的速度等于v1=vcosθ,则加速度

因θ逐渐减小,选项A正确.
解后语:本题考查加速度牵连关系,处理方法比速度要复杂得多,时有被错解(或歪打正着)的情况.一些基本函数(如三角函数sinθ、幂函数xn等)的微积分形式很常见,记住这些简单结论就可以解决不少问题.
【例4】(2003年高考上海卷第22题)如图3所示,OACO为置于水平面内的光滑闭合金属导轨,O,C处分别接有短电阻丝(图中用粗线表示),R1=4Ω、R2=8Ω,导轨其他部分电阻不计.导轨OAC的形状满足y=2sin(x)(单位:m).磁感应强度B=0.2T的匀强磁场垂直于导轨平面.一足够长的金属棒在水平外力作用下,以恒定的速率v=5.0 m/s水平向右在导轨上从O点滑动到C点,棒与导轨接触良好且始终保持与OC导轨垂直,不计棒的电阻.求:滑动过程中通过金属棒的电荷量有多少.
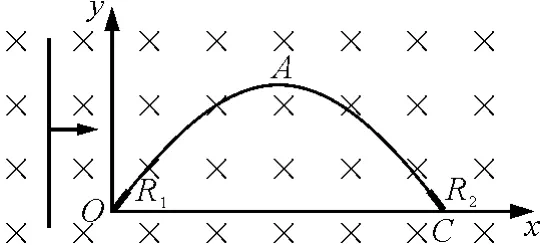
图3
解析:根据电磁感应定律

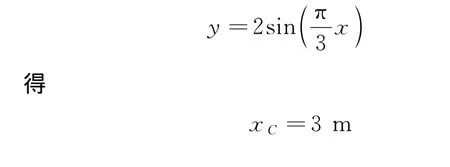

代入后得到
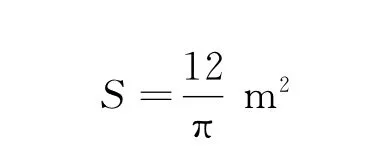
由此可得

【例5】(第22届全国中学生物理竞赛预赛第9题)如图4所示,水平放置的金属细圆环半径为a,竖直放置的金属细圆柱(其半径比a小得多)的端面与金属圆环的上表面在同一平面内,圆柱的细轴通过圆环的中心O.一质量为m,电阻为R的均匀导体细棒被圆环和细圆柱端面支撑,棒的一端有一小孔套在细轴O上,另一端A可绕轴线沿圆环作圆周运动,棒与圆环的摩擦因数为μ.圆环处于磁感应强度大小为B=Kr、方向竖直向上的恒定磁场中,式中K为大于零的常量,r为场点到轴线的距离.金属细圆柱与圆环用导线ed连接.不计棒与轴及与细圆柱端面的摩擦,也不计细圆柱、圆环及导线的电阻和感应电流产生的磁场.问沿垂直于棒的方向以多大的水平外力作用于棒的A端才能使棒以角速度ω匀速转动?
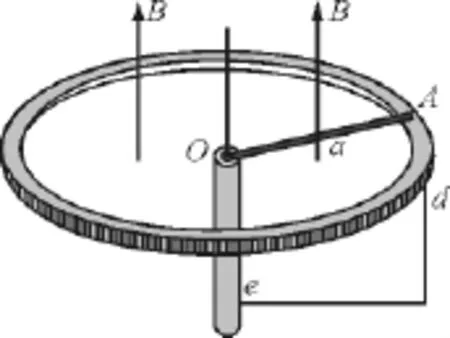
图4
分析:匀速转动应符合力矩平衡条件:M外=M安+M摩,为求安培力矩,关键是求出OA棒上的电动势.考虑一个周期T(OA棒转动一周)内,磁通量的变化量ΔΦ=BS,由于B是变化的,把它沿半径方向分割成若干个带状圆环,再积分即可.
解答:设沿OA向外第i个微元段的半径为r,该处带状圆环的电动势
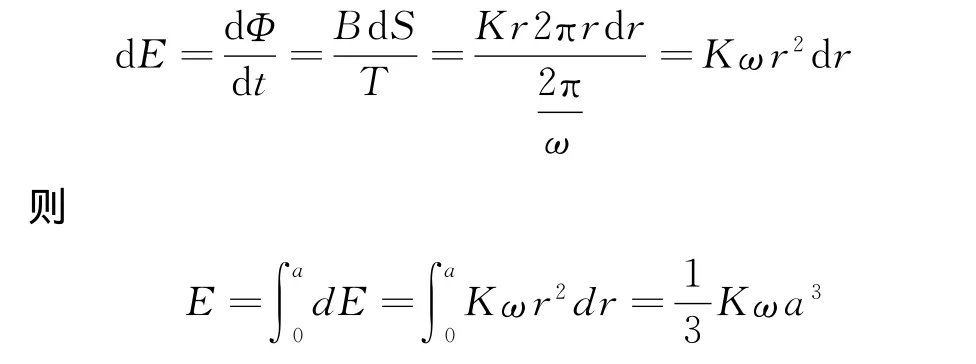
安培力矩

摩擦力矩
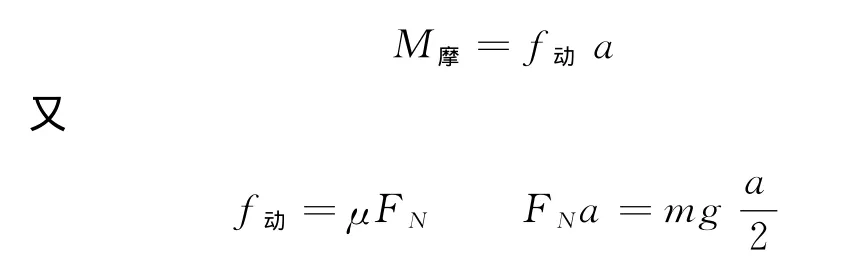
代入得
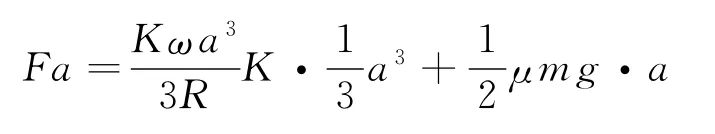
解得

解后语:在处理变量时,以前普遍采用微元法,其实质就是求导、积分的过程.涉及到两个以上的变量时(比如例5中B随着r变化,传统的方法是采用微元分割,借助高阶小量近似,写成相邻两项的差值,累加得到结果),用微元法需要有较高的技巧,而运用导数这一工具理应是最有效的.对于求OA棒上的电动势,本题还可采用以下解法:
第i个微元段的电动势
可见,求OA棒上的电动势,用积分方法会简洁一些.
1 杨国平.物理解题中的递推方法.物理通报,2012(5):56~59

